imported>Pascal |
imported>Billaude |
| Line 1: |
Line 1: |
| − | Currently the operators and basic predicates of the Event-B mathematical language supported by Rodin are fixed.
| + | = Objective = |
| − | We propose to extend Rodin to define basic predicates, new operators or new algebraic types.
| |
| | | | |
| − | == Requirements ==
| + | This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.<br> |
| | + | This reasoner discharges sequent whose goal denotes a membership which can be inferred from hypotheses. Here an basic example of what it discharges :<br> |
| | + | <math>H,\quad x\in S,\quad S\subset T,\quad T\subseteq U \quad\vdash x\in U</math> |
| | + | The other purpose of the reasoner is to have a condense proof tree (one step contain several inference rule). |
| | | | |
| − | === User Requirements === | + | = Analysis = |
| − | * Binary operators (prefix form, infix form or suffix form).
| |
| − | * Operators on boolean expressions.
| |
| − | * Unary operators, such as absolute values.
| |
| − | : Note that the pipe, which is already used for set comprehension, cannot be used to enter absolute values (''in fact, as in the new design the pipe used in set comprehension is only a syntaxic sugar, the same symbol may be used for absolute value. To be confirmed with the prototyped parser. It may however be not allowed in a first time until backtracking is implemented, due to use of lookahead making assumptions on how the pipe symbol is used. -Mathieu ).
| |
| − | * Basic predicates (e.g., the symmetry of relations <math>sym(R) \defi R=R^{-1}</math>).
| |
| − | : Having a way to enter such predicates may be considered as syntactic sugar, because it is already possible to use sets (e.g., <math>R \in sym</math>, where <math>sym \defi \{R \mid R=R ^{-1}\}</math>) or functions (e.g., <math>sym(R) = \True</math>, where <math>sym \defi (\lambda R \qdot R \in A \rel B \mid \bool(R = R^{-1}))</math>).
| |
| − | * Quantified expressions (e.g., <math>\sum x \qdot P \mid y</math>, <math>\prod x \qdot P \mid y</math>, <math>~\min(S)</math>, <math>~\max(S)</math>).
| |
| − | * Types.
| |
| − | ** Enumerated types.
| |
| − | ** Scalar types.
| |
| | | | |
| − | === User Input ===
| + | Such sequent are proved by PP and ML. But, these provers have both drawbacks : |
| − | The end-user shall provide the following information:
| + | *All the visible are added as needed hypotheses, which is most of the time not the case. |
| − | * keyboard input | + | *They take quite consequent time to prove it (even with the basic example given here above, the difference in time execution is noticeable). |
| − | * Lexicon and Syntax. <br/>More precisely, it includes the symbols, the form (prefix, infix, postfix), the grammar, associativity (left-associative or right associative), commutativity, priority, the mode (flattened or not), ... | + | *If there are too many hypotheses, or if the expression of the <math>x</math> is too complicated, they may not prove it. |
| − | * Pretty-print. <br/>Alternatively, the rendering may be determined from the notation parameters passed to the parser. | + | This is particularly true when in the list of inclusion expressions of each side of the relation are not equal. For example : <math>H,\quad a\in S,\quad S\subset T_1\cap T_2,\quad T_1\cup T_3\subseteq U\quad\vdash a\in U</math> |
| − | * Typing rules.
| + | <p> |
| − | * Well-definedness.
| + | Such a reasoner contributes to prove more Proof Obligations automatically, faster and with fewer needed hypotheses which makes proof rule more legible and proof replay less sensitive to modifications. |
| | | | |
| − | === Development Requirements === | + | = Design Decision = |
| − | * Scalability.
| |
| | | | |
| − | == Towards a generic AST == | + | == Tactic == |
| | | | |
| − | The following AST parts are to become generic, or at least parameterised:
| + | This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working. |
| − | * [[Constrained_Dynamic_Lexer | Lexer]]
| + | === Goal === |
| − | * [[Constrained Dynamic Parser | Parser]]
| + | The tactic (as the reasoner) should works only on goals such as : |
| − | * Nodes ( Formula class hierarchy ): parameters needed for:
| + | *<math>\cdots~\in~\cdots</math> |
| − | ** Type Solve (type rule needed to synthesize the type) | + | For examples : |
| − | ** Type Check (type rule needed to verify constraints on children types) | + | *<math>f(x)\in g\otimes h</math> |
| − | ** WD (WD predicate) | + | *<math>x\in A\cprod\left(B\cup C\right)</math> |
| − | ** PrettyPrint (tag image + notation (prefix, infix, postfix) + needs parentheses)
| + | *<math>x\mapsto y\in A\cprod B</math> |
| − | ** Visit Formula (getting children + visitor callback mechanism) | + | In the latter case, the reasoner won't try to prove that ''x'' belongs to ''A'' and ''y'' belongs to ''B'', but that the mapplet belong to the Cartesian product. |
| − | ** Rewrite Formula (associative formulæ have a specific flattening treatment) | + | === Hypotheses === |
| − | * Types (Type class hierarchy): parameters needed for: | + | Now we have to find hypotheses leading to discharge the sequent. To do so, the tactic recovers two kinds of hypotheses : |
| − | ** Building the type expression (type rule needed)
| + | #the ones related to the left member of the goal <math>\left( x\in S\right)</math> (this is the start point): |
| − | ** PrettyPrint (set operator image) | + | #*<math>x\in \cdots</math> |
| − | ** getting Base / Source / Target type (type rule needed) | + | #*<math>\cdots\mapsto x\mapsto\cdots\in\cdots</math> |
| − | * Verification of preconditions (see for example <tt>AssociativeExpression.checkPreconditions</tt>) | + | #*<math>\left\{\cdots, x,\cdots\right\}=/\subset/\subseteq\cdots</math> |
| | + | #*<math>\left\{\cdots, \cdots\mapsto x\mapsto\cdots,\cdots\right\}=/\subset/\subseteq\cdots</math> |
| | + | #*<math>f\ovl\left\{\cdots, x, \cdots\right\}=/\subset/\subseteq\cdots</math> |
| | + | #the ones denoting inclusion (all but the ones matching the description of the first point) : |
| | + | #*<math>\cdots\subset\cdots</math> |
| | + | #*<math>\cdots\subseteq\cdots</math> |
| | + | #*<math>\cdots=\cdots</math> |
| | + | Then, it will search a link between those hypotheses so that the sequent can be discharged. |
| | | | |
| − | === Vocabulary === | + | === Find a path === |
| | + | Now that we recovered all the hypotheses that could be useful for the reasoner, it remains to find a path among the hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. <math>f</math> always represent an expression (may be a domain, a range, etc.). |
| | + | #The following sequent is provable because <math>f\subseteq \varphi (f)</math>. |
| | + | #*<math>x\in f,\quad \varphi (f)\subseteq g\quad\vdash\quad x\in g</math> |
| | + | #*<math>\varphi (f) = f\quad\mid\quad f\cup h \quad\mid\quad h\cup f \quad\mid\quad h\ovl f</math> |
| | + | #The following sequent is provable because <math>\psi (f)\subseteq f</math>. |
| | + | #*<math>x\in \psi (f),\quad f\subseteq g\quad\vdash\quad x\in g</math> |
| | + | #*<math>\psi (f) = f\quad\mid\quad f\cap h \quad\mid\quad h\cap f \quad\mid\quad f\setminus h \quad\mid\quad f\ransub A \quad\mid\quad f\ranres A \quad\mid\quad A\domsub f \quad\mid\quad A\domres f</math> |
| | + | #We can generalized the first two points. This is the Russian dolls system. We can easily prove a sequent with multiple inclusions by going from hypothesis to hypothesis. |
| | + | #*<math>x\in \psi (f),\quad \varphi (f)\subseteq g\quad\vdash\quad x\in g</math> |
| | + | #For some relations, [[#positions|positions]] are needed to be known to continue to find hypotheses, but it is not always necessary. |
| | + | #*<math>x\mapsto y\in f,\quad f\subseteq A\cprod B\quad\vdash\quad x\in A</math> |
| | + | #*<math>x\in dom(f),\quad f\subseteq A\cprod B\quad\vdash\quad x\in A</math> |
| | + | #*<math>x\in ran(f),\quad f\subseteq A\cprod B\quad\vdash\quad x\in B</math> |
| | | | |
| − | An '''extension''' is to be understood as a single additional operator definition.
| + | By using these inclusion and rewrites, it tries to find a path among the recovered hypotheses. Every one of those should only be used once, avoiding possible infinite loop <math>\left(A\subseteq B,\quad B\subseteq A\right)</math>. Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input. |
| | | | |
| − | === Tags === | + | == Reasoner == |
| | | | |
| − | Every extension is associated with an integer tag, just like existing operators. Thus, questions arise about how to allocate new tags and how to deal with existing tags.<br />
| + | The way the reasoner must work is still in discussion. |
| − | The solution proposed here consists in keeping existing tags 'as is'. They are already defined and hard coded in the <tt>Formula</tt> class, so this choice is made with backward compatibility in mind. | |
| | | | |
| − | Now concerning extension tags, we will first introduce a few hypotheses:
| + | = Implementation = |
| − | * Tags_Hyp1: tags are never persisted across sessions on a given platform
| |
| − | * Tags_Hyp2: tags are never referenced for sharing purposes across various platforms
| |
| − | In other words, cross-platform/session formula references are always made through their ''String'' representation. These assumptions, which were already made and verified for Rodin before extensions, lead us to restrict further considerations to the scope of a single session on a single platform.
| |
| | | | |
| − | The following definitions hold at a given instant <math>t</math> and for the whole platform.<br />
| + | This section explain how the tactic has bee implemented. |
| − | Let <math>\mathit{EXTENSION}_t</math> be the set of extensions supported by the platform at instant <math>t</math>;<br /> let <math>\mathit{tag}_t</math> denote the affectation of tags to a extensions at instant <math>t</math> (<math>\mathit{tag}_t \in \mathit{EXTENSION}_t \pfun \intg</math>);<br /> let <math>\mathit{COMMON}</math> be the set of existing tags defined by the <tt>Formula</tt> class (<math>\mathit{COMMON} \sub \intg</math>).<br /> The following requirements emerge:
| |
| − | * Tags_Req1: <math>\forall t \qdot \mathit{tag}_t \in \mathit{EXTENSION}_t \tinj \intg</math>
| |
| − | * Tags_Req2: <math>\forall e, t_1,t_2 \qdot \mathit{tag}_{t_1}(e)=\mathit{tag}_{t_2}(e)</math> where <math>t_1, t_2</math> are two instants during a given session
| |
| − | * Tags_Req3: <math>\forall t \qdot \ran(\mathit{tag}_t) \cap \mathit{COMMON} = \empty</math>
| |
| | | | |
| − | The above-mentioned scope-restricting hypothesis can be reformulated into: <math>\mathit{tag}</math> needs not be stable across sessions nor across platforms.
| + | === Positions === |
| | + | As it was said, we may sometimes need the position. It is represented by an array of integer. Here are the possible values the array contains (atomic positions) : |
| | + | * '''''kdom''''' : it corresponds to the domain. |
| | + | **<math>\left[A\cprod B\right]_{pos\;=\;kdom} = A</math> |
| | + | **<math>\left[x\mapsto y\right]_{pos\;=\;kdom} = x</math> |
| | + | **<math>\left[g\right]_{pos\;=\;kdom} = dom(g)</math> |
| | + | * '''''kran''''' : it corresponds to the domain. |
| | + | **<math>\left[A\cprod B\right]_{pos\;=\;kran} = B</math> |
| | + | **<math>\left[x\mapsto y\right]_{pos\;=\;kran} = y</math> |
| | + | **<math>\left[g\right]_{pos\;=\;kran} = ran(g)</math> |
| | + | * '''''converse''''' : it corresponds to the child of an inverse |
| | + | **<math>\left[f^{-1}\right]_{pos\;=\;converse}=f</math> |
| | + | **<math>\left[A\cprod B\right]_{pos\;=\;converse} = B\cprod A</math> |
| | + | For example, the following expressions at the given positions are equivalent. |
| | + | :<math>\left[ran(dom(g))\right]_{pos\;=\;\left[\right]} = \left[dom(g)\right]_{pos\;=\;\left[kran\right]} = \left[g\right]_{pos\;=\;\left[kdom,\; kran\right]}</math> |
| | | | |
| − | === Formula Factory === | + | Some combinations of atomic positions are equivalent. In order to simplify comparison between positions, they are normalized : |
| | + | *<math>ran(f^{-1}) = dom(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kran\right]} = \left[f\right]_{pos\;=\;\left[kdom\right]}</math> |
| | + | *<math>dom(f^{-1}) = ran(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kdom\right]} = \left[f\right]_{pos\;=\;\left[kran\right]}</math> |
| | + | *<math>\left(f^{-1}\right)^{-1} = f\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~converse\right]} = \left[f\right]_{pos\;=\;\left[~\right]}</math> |
| | | | |
| − | The requirements about tags give rise to a need for centralising the <math>\mathit{tag}</math> relation in order to enforce tag uniqueness.
| + | === Goal === |
| − | The Formula Factory appears to be a convenient and logical candidate for playing this role. Each time an extension is used to make a formula, the factory is called and it can check whether its associated tag exists, create it if needed, then return the new extended formula while maintaining tag consistency.
| |
| | | | |
| − | The factory can also provide API for requests about tags and extensions: getting the tag from an extension and conversely.
| + | As explained in the design decision part, goal is checked. If it matches the description here above <math>\left(x\in S\right)</math> then ''x'' is stored in an attribute. Moreover, from the set ''S'', we compute every pair ''expression'' & ''position'' equivalent to it. For example, from the set <math>dom(ran(ran(g)))</math>, the map will be computed : |
| | + | *<math>dom(ran(ran(g)))\;\mapsto\;[\;]</math> |
| | + | *<math>ran(ran(g))\;\mapsto\;[kdom]</math> |
| | + | *<math>ran(g)\;\mapsto\;[kran,~kdom]</math> |
| | + | *<math>g\;\mapsto\;[kran,~kran,~kdom]</math> |
| | | | |
| − | We also need additional methods to create extended formulæ. A first problem to address is: which type should these methods return ?
| + | A pair (expression ; position) is said equal to the goal if and only if there exists a pair equivalent to the goal (GoalExp ; GoalPos) and a pair equivalent to the given pair (Exp ; Pos) such as ''Pos = GoalPos'' and ''Exp'' is contained in ''GoalExp''. |
| − | We could define as many extended types as the common AST API does, namely <tt>ExtendedUnaryPredicate</tt>, <tt>ExtendedAssociativeExpression</tt>, and so on, but this would lead to a large number of new types to deal with (in visitors, filters, …), together with a constraint about which types extensions would be forced to fit into. It is thus preferable to have as few extended types as possible, but with as much parameterisation as can be. Considering that the two basic types <tt>Expression</tt> and <tt>Predicate</tt> have to be extensible, we come to add two extended types <tt>ExtendedExpression</tt> and <tt>ExtendedPredicate</tt>.
| |
| | | | |
| − | ExtendedExpression makeExtendedExpression( ? )
| + | === Hypotheses === |
| − | ExtendedPredicate makeExtendedPredicate( ? )
| |
| | | | |
| − | Second problem to address: which arguments should these methods take ?
| + | As explained in the design decision part, there are two kinds of hypotheses which are recovered. But when hypotheses related to the left member of the goal <math>\left(x\in S\right)</math> are stored, the position of ''x'' is also record. Then, if there is an hypothesis such as <math>\left\{\cdots\;,\;y\mapsto x\mapsto z\;,\;m\mapsto x\;,\;\cdots\right\} = A</math>, then this hypothesis is mapped to the positions <math>\left\{\left[0,~1\right],~\left[1\right]\right\}</math>. |
| − | Other factory methods take the tag, a collection of children where applicable, and a source location. In order to discuss what can be passed as argument to make extended formulæ, we have to recall that the <tt>make…</tt> factory methods have various kinds of clients, namely:
| |
| − | * parser
| |
| − | * POG
| |
| − | * provers
| |
| − | (other factory clients use the parsing or identifier utility methods: SC modules, indexers, …)
| |
| | | | |
| − | Thus, the arguments should be convenient for clients, depending on which information they have at hand.
| + | === Find a path === |
| − | The source location does not obviously seem to require any adaptation and can be taken as argument the same way. Concerning the tag, it depends on whether clients have a tag or an extension at hand. Both are intended to be easily retrieved from the factory. As a preliminary choice, we can go for the tag and adjust this decision when we know more about client convenience.
| |
| | | | |
| − | As for children, the problem is more about their types. We want to be able to handle as many children as needed, and of all possible types. Looking to existing formula children configurations, we can find:
| + | Let's considered the sequent with the following goal : <math>x\in V</math>. |
| − | * expressions with predicate children: <math>\mathit{bool}(P)</math>
| + | We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position <math>pos</math> and the set <math>S</math> as explained in [[#Hypotheses|hypotheses]]. Then, for each equivalent pair to these one <math>\left(S', pos'\right)</math>, we compute set containing <math>S'</math> ([[#Design Decision#Tactic#Find a path| Find a path 2.]]). For every new pair, we test if it is contained in the goal. |
| − | * expressions with expression children: <math>E_1 + E_2</math>
| |
| − | * predicates with predicate children: <math>P_1 \limp P_2</math>
| |
| − | * predicates with expression children: <math>\mathit{partition}(S, E_1, E_2)</math>
| |
| − | * mixed operators: <math>\{x \qdot P(x) \mid E(x)\}</math>, but it is worth noting that the possibility of introducing bound variables in extended formulæ is not established yet.
| |
| − | Thus, for the sake of generality, children of both types should be supported for both extended predicates and extended expressions.
| |
| | | | |
| − | ExtendedExpression makeExtendedExpression(int tag, Expression[] expressions, Predicate[] predicates, SourceLocation location)
| + | To be continued. |
| − | ExtendedPredicate makeExtendedPredicate(int tag, Expression[] expressions, Predicate[] predicates, SourceLocation location)
| |
| | | | |
| − | === Defining Extensions === | + | = Untreated cases = |
| | | | |
| − | An extension is meant to contain every information and behaviour required by:
| + | Some cases are not treated. Further enhancement may be provided for some. |
| − | * Keyboard
| + | *<math>x\in f,\quad f\in A\;op\;B\quad\vdash\quad x\in A\cprod B</math> |
| − | * (Extensible Fonts ?)
| + | *<math>x\in f\otimes g,\quad f\subseteq A\cprod B,\quad g\subseteq C\cprod D\quad\vdash\quad x\in (A\cprod C)\cprod(B\cprod D)</math> |
| − | * Lexer
| + | *<math>x\in f\otimes g,\quad f\subseteq h\quad\vdash\quad x\in h\otimes g</math> |
| − | * Parser
| + | *<math>x\in \left\{a,~b,~c\right\},\quad\left\{a,~b,~c,~d,~e,~f\right\}\subseteq D\quad\vdash\quad x\in D</math> |
| − | * AST
| + | *<math>x\in A\cprod B,\quad A\subseteq C\quad\vdash\quad x\in C\cprod B</math> |
| − | * Static Checker
| + | *<math>x\in dom(f)\cap A\quad\vdash\quad x\in dom(A\domres f)</math> |
| − | * Proof Obligation Generator
| + | *<math>x\in ran(f)\cap A\quad\vdash\quad x\in ran(f\ranres A)</math> |
| − | * Provers
| + | *<math>x\in dom(A\domres f)\quad\vdash\quad x\in dom(f)\cap A</math> |
| − | | + | *<math>x\in ran(f\ranres A)\quad\vdash\quad x\in ran(f)\cap A</math> |
| − | ==== Keyboard requirements ====
| + | *<math>x\in \quad\vdash\quad</math> |
| − | | + | *<math>\quad\vdash\quad</math> |
| − | '''Kbd_req1''': an extension must provide an association combo/translation for every uncommon symbol involved in the notation.
| + | *<math>\quad\vdash\quad</math> |
| − | | + | *<math>\quad\vdash\quad</math> |
| − | ==== Lexer requirements ====
| + | *:<math>\bigl(</math> where <math>op_1</math> and <math>op_2</math> are ones of :<math>\quad\rel, \trel, \srel, \strel, \pfun, \tfun, \pinj, \tinj, \psur, \tsur, \tbij\bigr)</math> |
| − | | |
| − | '''Lex_req1''': an extension must provide an association lexeme/token for every uncommon symbol involved in the notation.
| |
| − | | |
| − | ==== Parser requirements ====
| |
| − | | |
| − | According to the [[Constrained_Dynamic_Parser| Parser]] page, the following informations are required by the parser in order to be able to parse a formula containing a given extension.
| |
| − | | |
| − | * symbol compatibility
| |
| − | * group compatibility
| |
| − | * symbol precedence
| |
| − | * group precedence
| |
| − | * notation (see below)
| |
| − | | |
| − | ==== AST requirements ====
| |
| − | | |
| − | The following hard-coded concepts need to be reified for supporting extensions in the AST. An extension instance will then provide these reified informations to an extended formula class for it to be able to fulfil its API. It is the expression of the missing information for a <tt>ExtendedExpression</tt> (resp. <tt>ExtendedPredicate</tt>) to behave as a <tt>Expression</tt> (resp. <tt>Predicate</tt>). It can also be viewed as the parametrization of the AST.
| |
| − | | |
| − | ===== Notation =====
| |
| − | | |
| − | The notation defines how the formula will be printed. In this document, we use the following convention:
| |
| − | * <math>e_i</math> is the i-th child expression of the extended formula | |
| − | * <math>p_i</math> is the i-th child predicate of the extended formula
| |
| − | | |
| − | ''Example'': infix operator "<math>\lozenge</math>"
| |
| − | <math>e_1 \lozenge e_2 \lozenge \ldots \lozenge e_n</math>
| |
| − | | |
| − | We define the following notation framework:
| |
| − | | |
| − | [[Image:notation_uml.png]]
| |
| − | | |
| − | On the "<math>\lozenge</math>" infix operator example, the iterable notation would return sucessively:
| |
| − | * a <tt>IFormulaChild</tt> with index 1
| |
| − | * the <tt>INotationSymbol</tt> "<math>\lozenge</math>" | |
| − | * a <tt>IFormulaChild</tt> with index 2
| |
| − | * the <tt>INotationSymbol</tt> "<math>\lozenge</math>"
| |
| − | * …
| |
| − | * a <tt>IFormulaChild</tt> with index <math>n</math>
| |
| − | | |
| − | For the iteration not to run forever, the limit <math>n</math> needs to be known: this is the role of the <tt>mapsTo()</tt> method, which fixes the number of children, called when this number is known (i.e. for a particular formula instance).
| |
| − | | |
| − | '''Open question''': how to integrate bound identifier lists in the notation?
| |
| − | | |
| − | We may make a distinction between fixed-size notations (like n-ary operators for a given n) and variable-size notations (like associative infix operators).
| |
| − | While fixed-size notations would have no specific expressivity limitations (besides parser conflicts with other notations), only a finite set of pre-defined variable-size notation patterns will be proposed to the user.
| |
| − | | |
| − | The following features need to be implemented to support the notation framework:
| |
| − | * special meta variables that represent children (<math>e_i</math>, <math>p_i</math>)
| |
| − | * a notation parser that extracts a fixed-size notation pattern from a user input string | |
| − | | |
| − | ===== Well-Definedness =====
| |
| − | | |
| − | WD predicates also are user-provided data.
| |
| − | | |
| − | ''Example'':
| |
| − | <math>\mathit{D}(e_1) \land (\forall i \cdot i \in 1\mathit{..}(n-1) \Rightarrow (\mathit{D}(e_i) \Rightarrow \mathit{D}(e_{i+1})))</math>
| |
| − | | |
| − | In order to process WD predicates, we need to add the following features to the AST:
| |
| − | * the <math>\mathit{D}</math> operator | |
| − | * expression variables (predicate variables already exist) | |
| − | * special expression variables and predicate variables that denote a particular formula child (we need to refer to <math>e_1</math> and <math>e_i</math> in the above example)
| |
| − | * a <tt>parse()</tt> method that accepts these special meta variables and the <math>\mathit{D}</math> operator that returns a <tt>Predicate</tt> (a WD predicate pattern)
| |
| − | * a <tt>makeWDPredicate(aWDPredicatePattern, aPatternInstantiation)</tt> method that makes an actual WD predicate
| |
| − | | |
| − | ===== Type Check =====
| |
| − | | |
| − | An extension shall give a type rule, which consists in:
| |
| − | * type check predicates (addressed in this section)
| |
| − | * a resulting type expression (only for expressions) | |
| − | | |
| − | ''Example'':
| |
| − | <math>(\forall i \cdot \mathit{type}(e_i) = \pow(\alpha)) \land (\forall i,j \cdot \mathit{type}(e_i)=\mathit{type}(e_j))</math>
| |
| − | | |
| − | Type checking can be reified provided the following new AST features:
| |
| − | * the <math>\mathit{type}</math> operator | |
| − | * type variables (<math>\alpha</math>)
| |
| − | * the above-mentioned expression variables and predicate variables
| |
| − | * a <tt>parse()</tt> method that accepts these special meta variables and the <math>\mathit{type}</math> operator and returns a <tt>Predicate</tt> (a Type predicate pattern)
| |
| − | * a <tt>makeTypePredicate(aTypePredicatePattern, aPatternInstantiation)</tt> method that makes an actual Type predicate | |
| − | | |
| − | ===== Type Solve =====
| |
| − | | |
| − | This section addresses type synthesizing for extended expressions (the resulting type part of a type rule). It is given as a type expression pattern, so that the actual type can be computed from the children.
| |
| − | | |
| − | ''Example'':
| |
| − | <math>\pow(\mathit{type}(e_1))</math>
| |
| − | | |
| − | In addition to the requirements for Type Check, the following features are needed:
| |
| − | * a <tt>parse()</tt> method that accepts special meta variables and the <math>\mathit{type}</math> operator and returns an <tt>Expression</tt> (a Type Expression Pattern) | |
| − | * a <tt>makeTypeExpression(aTypeExpressionPattern, aPatternInstantiation)</tt> method that makes an actual Type expression | |
| − | | |
| − | ==== Static Checker requirements ====
| |
| − | {{TODO}}
| |
| − | ==== Proof Obligation Generator requirements ====
| |
| − | {{TODO}}
| |
| − | ==== Provers requirements ====
| |
| − | {{TODO}}
| |
| − | | |
| − | === Extension compatibility issues ===
| |
| − | {{TODO}}
| |
| − | | |
| − | == User Input Summarization ==
| |
| − | | |
| − | Identified required data entail the following user input:
| |
| − | | |
| − | {{TODO}}
| |
| − | | |
| − | == Impact on other tools ==
| |
| − | | |
| − | Impacted plug-ins (use a factory to build formulæ):
| |
| − | * <tt>org.eventb.core</tt> | |
| − | : In particular, the static checker and proof obligation generator are impacted.
| |
| − | * <tt>org.eventb.core.seqprover</tt> | |
| − | * <tt>org.eventb.pp</tt>
| |
| − | * <tt>org.eventb.pptrans</tt>
| |
| − | * <tt>org.eventb.ui</tt>
| |
| − | | |
| − | == Identified Problems ==
| |
| − | The parser shall enforce verifications to detect the following situations:
| |
| − | * Two mathematical extensions are not compatible (the extensions define symbols with the same name but with a different semantics).
| |
| − | * A mathematical extension is added to a model and there is a conflict between a symbol and an identifier.
| |
| − | * An identifier which conflicts with a symbol of a visible mathematical extension is added to a model.
| |
| − | | |
| − | Beyond that, the following situations are problematic:
| |
| − | * A formula has been written with a given parser configuration and is read with another parser configuration.
| |
| − | : As a consequence, it appears as necessary to remember the parser configuration.
| |
| − | : The static checker will then have a way to invalid the sources of conflicts (e.g., priority of operators, etc).
| |
| − | :: ''The static checker will then have a way to invalid the formula upon detecting a conflict (name clash, associativity change, semantic change...) [[User:Mathieu|mathieu]]
| |
| − | | |
| − | * A proof may free a quantified expression which is in conflict with a mathematical extension.
| |
| − | : SOLUTION #1: Renaming the conflicting identifiers in proofs?
| |
| − | | |
| − | == Open Questions ==
| |
| − | | |
| − | === New types ===
| |
| − | Which option should we prefer for new types?
| |
| − | * OPTION #1: Transparent mode. | |
| − | :In transparent mode, it is always referred to the base type. As a consequence, the type conversion is implicitly supported (weak typing).
| |
| − | :For example, it is possible to define the <tt>DISTANCE</tt> and <tt>SPEED</tt> types, which are both derived from the <math>\intg</math> base type, and to multiply a value of the former type with a value of the latter type.
| |
| − | | |
| − | * OPTION #2: Opaque mode.
| |
| − | :In opaque mode, it is never referred to the base type. As a consequence, values of one type cannot be converted to another type (strong typing).
| |
| − | :Thus, the above multiplication is not allowed.
| |
| − | :This approach has at least two advantages:
| |
| − | :* Stronger type checking.
| |
| − | :* Better prover performances.
| |
| − | :It also has some disadvantages:
| |
| − | :* need of ''extractors'' to convert back to base types.
| |
| − | :* need of extra circuitry to allow things like <math>x:=d*2</math> where <math>x, d</math> are of type <tt>DISTANCE</tt>
| |
| − | | |
| − | * OPTION #3: Mixed mode.
| |
| − | :In mixed mode, the transparent mode is applied to scalar types and the opaque mode is applied to other types.
| |
| − | | |
| − | === Scope of the mathematical extensions ===
| |
| − | * OPTION #1: Project scope.
| |
| − | :The mathematical extensions are implicitly visible to all components of the project that has imported them.
| |
| − | * OPTION #2: Component scope.
| |
| − | :The mathematical extensions are only visible to the components that have explicitly imported them. However, note that this visibility is propagated through the hierarchy of contexts and machines (<tt>EXTENDS</tt>, <tt>SEES</tt> and <tt>REFINES</tt> clauses).
| |
| − | :An issue has been identified. Suppose that <tt>ext1</tt> extension is visible to component <tt>C1</tt> and <tt>ext2</tt> is visible to component <tt>C2</tt>, and there is no compatibility issue between <tt>ext1</tt> and <tt>ext2</tt>. It is not excluded that an identifier declared in <tt>C1</tt> conflict with a symbol in <tt>ext2</tt>. As a consequence, a global verification is required when adding a new mathematical extension.
| |
| − | | |
| − | == Bibliography ==
| |
| − | * J.R. Abrial, M.Butler, M.Schmalz, S.Hallerstede, L.Voisin, [http://deploy-eprints.ecs.soton.ac.uk/80 ''Proposals for Mathematical Extensions for Event-B''], 2009.
| |
| − | :This proposal consists in considering three kinds of extension:
| |
| − | # Extensions of set-theoretic expressions or predicates: example extensions of this kind consist in adding the transitive closure of relations or various ordered relations.
| |
| − | # Extensions of the library of theorems for predicates and operators.
| |
| − | # Extensions of the Set Theory itself through the definition of algebraic types such as lists or ordered trees using new set constructors.
| |
| | | | |
| | [[Category:Design proposal]] | | [[Category:Design proposal]] |
Objective
This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.
This reasoner discharges sequent whose goal denotes a membership which can be inferred from hypotheses. Here an basic example of what it discharges :
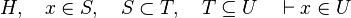 The other purpose of the reasoner is to have a condense proof tree (one step contain several inference rule).
The other purpose of the reasoner is to have a condense proof tree (one step contain several inference rule).
Analysis
Such sequent are proved by PP and ML. But, these provers have both drawbacks :
- All the visible are added as needed hypotheses, which is most of the time not the case.
- They take quite consequent time to prove it (even with the basic example given here above, the difference in time execution is noticeable).
- If there are too many hypotheses, or if the expression of the
 is too complicated, they may not prove it.
is too complicated, they may not prove it.
This is particularly true when in the list of inclusion expressions of each side of the relation are not equal. For example : 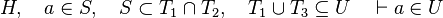
Such a reasoner contributes to prove more Proof Obligations automatically, faster and with fewer needed hypotheses which makes proof rule more legible and proof replay less sensitive to modifications.
Design Decision
Tactic
This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working.
Goal
The tactic (as the reasoner) should works only on goals such as :
For examples :
In the latter case, the reasoner won't try to prove that x belongs to A and y belongs to B, but that the mapplet belong to the Cartesian product.
Hypotheses
Now we have to find hypotheses leading to discharge the sequent. To do so, the tactic recovers two kinds of hypotheses :
- the ones related to the left member of the goal
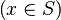 (this is the start point):
(this is the start point):
- the ones denoting inclusion (all but the ones matching the description of the first point) :
Then, it will search a link between those hypotheses so that the sequent can be discharged.
Find a path
Now that we recovered all the hypotheses that could be useful for the reasoner, it remains to find a path among the hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. 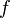 always represent an expression (may be a domain, a range, etc.).
always represent an expression (may be a domain, a range, etc.).
- The following sequent is provable because
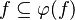 .
.
- The following sequent is provable because
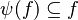 .
.
- We can generalized the first two points. This is the Russian dolls system. We can easily prove a sequent with multiple inclusions by going from hypothesis to hypothesis.
- For some relations, positions are needed to be known to continue to find hypotheses, but it is not always necessary.
By using these inclusion and rewrites, it tries to find a path among the recovered hypotheses. Every one of those should only be used once, avoiding possible infinite loop  . Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
. Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
Reasoner
The way the reasoner must work is still in discussion.
Implementation
This section explain how the tactic has bee implemented.
Positions
As it was said, we may sometimes need the position. It is represented by an array of integer. Here are the possible values the array contains (atomic positions) :
- kdom : it corresponds to the domain.
- kran : it corresponds to the domain.
- converse : it corresponds to the child of an inverse
For example, the following expressions at the given positions are equivalent.
![\left[ran(dom(g))\right]_{pos\;=\;\left[\right]} = \left[dom(g)\right]_{pos\;=\;\left[kran\right]} = \left[g\right]_{pos\;=\;\left[kdom,\; kran\right]}](/images/math/1/5/7/1578bdb9722f70811943df524818d8d8.png)
Some combinations of atomic positions are equivalent. In order to simplify comparison between positions, they are normalized :
Goal
As explained in the design decision part, goal is checked. If it matches the description here above 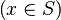 then x is stored in an attribute. Moreover, from the set S, we compute every pair expression & position equivalent to it. For example, from the set
then x is stored in an attribute. Moreover, from the set S, we compute every pair expression & position equivalent to it. For example, from the set 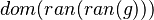 , the map will be computed :
, the map will be computed :
A pair (expression ; position) is said equal to the goal if and only if there exists a pair equivalent to the goal (GoalExp ; GoalPos) and a pair equivalent to the given pair (Exp ; Pos) such as Pos = GoalPos and Exp is contained in GoalExp.
Hypotheses
As explained in the design decision part, there are two kinds of hypotheses which are recovered. But when hypotheses related to the left member of the goal 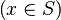 are stored, the position of x is also record. Then, if there is an hypothesis such as
are stored, the position of x is also record. Then, if there is an hypothesis such as 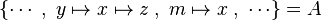 , then this hypothesis is mapped to the positions
, then this hypothesis is mapped to the positions ![\left\{\left[0,~1\right],~\left[1\right]\right\}](/images/math/9/8/f/98f4b25272ac46fc08b6f57cec71d01a.png) .
.
Find a path
Let's considered the sequent with the following goal : 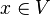 .
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position
.
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position 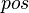 and the set
and the set  as explained in hypotheses. Then, for each equivalent pair to these one
as explained in hypotheses. Then, for each equivalent pair to these one 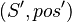 , we compute set containing
, we compute set containing 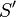 ( Find a path 2.). For every new pair, we test if it is contained in the goal.
( Find a path 2.). For every new pair, we test if it is contained in the goal.
To be continued.
Untreated cases
Some cases are not treated. Further enhancement may be provided for some.
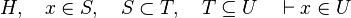 The other purpose of the reasoner is to have a condense proof tree (one step contain several inference rule).
The other purpose of the reasoner is to have a condense proof tree (one step contain several inference rule).
 is too complicated, they may not prove it.
is too complicated, they may not prove it.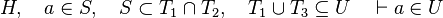
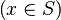 (this is the start point):
(this is the start point):
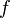 always represent an expression (may be a domain, a range, etc.).
always represent an expression (may be a domain, a range, etc.).
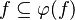 .
.
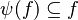 .
.
 . Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
. Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
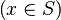 then x is stored in an attribute. Moreover, from the set S, we compute every pair expression & position equivalent to it. For example, from the set
then x is stored in an attribute. Moreover, from the set S, we compute every pair expression & position equivalent to it. For example, from the set 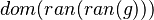 , the map will be computed :
, the map will be computed :
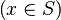 are stored, the position of x is also record. Then, if there is an hypothesis such as
are stored, the position of x is also record. Then, if there is an hypothesis such as 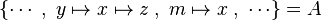 , then this hypothesis is mapped to the positions
, then this hypothesis is mapped to the positions ![\left\{\left[0,~1\right],~\left[1\right]\right\}](/images/math/9/8/f/98f4b25272ac46fc08b6f57cec71d01a.png) .
.
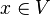 .
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position
.
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position 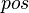 and the set
and the set  as explained in hypotheses. Then, for each equivalent pair to these one
as explained in hypotheses. Then, for each equivalent pair to these one 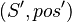 , we compute set containing
, we compute set containing 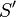 ( Find a path 2.). For every new pair, we test if it is contained in the goal.
( Find a path 2.). For every new pair, we test if it is contained in the goal.
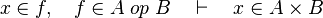
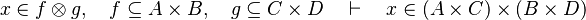
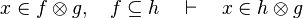
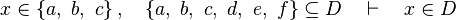
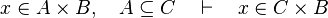
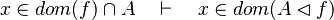
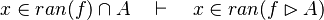
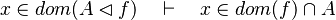
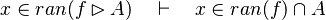
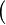 where
where 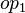 and
and 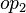 are ones of :
are ones of :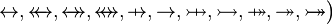
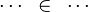
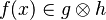
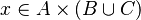
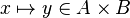
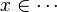
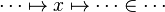
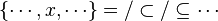
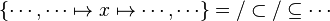
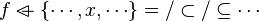
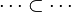
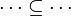

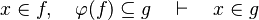

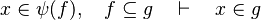

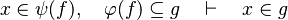
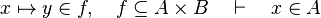
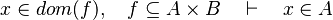
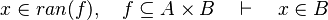
![\left[A\cprod B\right]_{pos\;=\;kdom} = A](/images/math/5/c/9/5c9188384893a5f785386fd9be5f5211.png)
![\left[x\mapsto y\right]_{pos\;=\;kdom} = x](/images/math/2/0/2/202d5f1c44ca4d283d912b36a0363bdb.png)
![\left[g\right]_{pos\;=\;kdom} = dom(g)](/images/math/9/e/8/9e8243fbfbf64a5fbf4dd9c86a803249.png)
![\left[A\cprod B\right]_{pos\;=\;kran} = B](/images/math/5/1/e/51e9dde2c7714a18994bfd88133abaff.png)
![\left[x\mapsto y\right]_{pos\;=\;kran} = y](/images/math/a/f/9/af9a897a8826985891b874f9b9909e12.png)
![\left[g\right]_{pos\;=\;kran} = ran(g)](/images/math/7/f/1/7f1b4c4c2ce799142d20e081fab53cff.png)
![\left[f^{-1}\right]_{pos\;=\;converse}=f](/images/math/f/6/d/f6d099908d10e496857d491b0ee6bca9.png)
![\left[A\cprod B\right]_{pos\;=\;converse} = B\cprod A](/images/math/5/5/8/5580559f9c30df0338362d5a49c66335.png)
![\left[ran(dom(g))\right]_{pos\;=\;\left[\right]} = \left[dom(g)\right]_{pos\;=\;\left[kran\right]} = \left[g\right]_{pos\;=\;\left[kdom,\; kran\right]}](/images/math/1/5/7/1578bdb9722f70811943df524818d8d8.png)
![ran(f^{-1}) = dom(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kran\right]} = \left[f\right]_{pos\;=\;\left[kdom\right]}](/images/math/9/a/b/9ab2c57a971be9093b74331cfdf365f2.png)
![dom(f^{-1}) = ran(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kdom\right]} = \left[f\right]_{pos\;=\;\left[kran\right]}](/images/math/d/1/4/d145100f50452d20541cbc2113d8a9c4.png)
![\left(f^{-1}\right)^{-1} = f\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~converse\right]} = \left[f\right]_{pos\;=\;\left[~\right]}](/images/math/f/f/2/ff2fe24f0d2d75efe4839f2d2bfe2130.png)
![dom(ran(ran(g)))\;\mapsto\;[\;]](/images/math/8/9/6/896c9400150a21f66969511b65b17aff.png)
![ran(ran(g))\;\mapsto\;[kdom]](/images/math/f/8/d/f8decb246a1ce1188fcc89f4c3a86552.png)
![ran(g)\;\mapsto\;[kran,~kdom]](/images/math/3/4/b/34b4296ddfda3dee3084fe62a3bac0d2.png)
![g\;\mapsto\;[kran,~kran,~kdom]](/images/math/3/8/2/382eeb6cc9956a0443234c7fffe4e405.png)