UML-B FAQ: Difference between revisions
imported>Colin No edit summary |
imported>Mathieu |
||
| (One intermediate revision by one other user not shown) | |||
| Line 12: | Line 12: | ||
[[Image:fixedClassInstances.png]] | [[Image:fixedClassInstances.png]] | ||
Of course, for this example, you could obtain a much simpler model by leaving out the explicit modelling of bridge, island and mainland | Of course, for this example, you could obtain a much simpler model by leaving out the explicit modelling of bridge, island and mainland, but the advantage of our model is that it can easily be extended to deal with different configurations having several bridges and islands. | ||
[[Category:User FAQ]] | |||
[[Category:UML-B]] | |||
Latest revision as of 22:23, 11 December 2008
How should I model a fixed set of instances with a class?
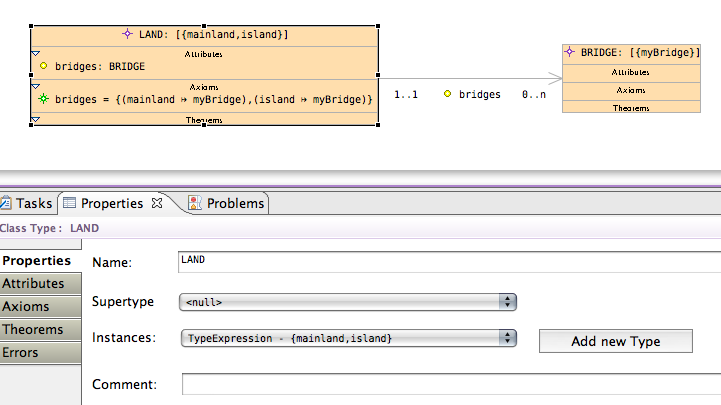
It is often useful to use a class to model a small, fixed set of instances. (As opposed to an indeterminate variable set where instances are constructed dynamically). For example, to model a bridge between a mainland and an island, I would define a new class type BRIDGE and enumerate it with a constant, "myBridge" (i.e. Instances = {myBridge} where {myBridge} has been added as a type expression using the add new type button). I might also define the mainland and island this way as instances of a class type, LAND, and use an association to represent the connection of LAND to BRIDGE. (My model loses the generic distinction between mainlands and islands, so you might prefer to use 2 seperate classtypes). I would do all this in a Context diagram rather than a class diagram. That way it represents contextual configuration data, rather than state variables.
To specify the association exactly, I could add axioms to define the actual mapping of mainland and island to myBridge. However, be careful because if this specific data conflicts with the more general definition of bridges the prover will not work properly. (It would be better if the type axiom for bridges was minimal and the cardinality restrictions (bijection in this case) were made into Theorems to be proved).
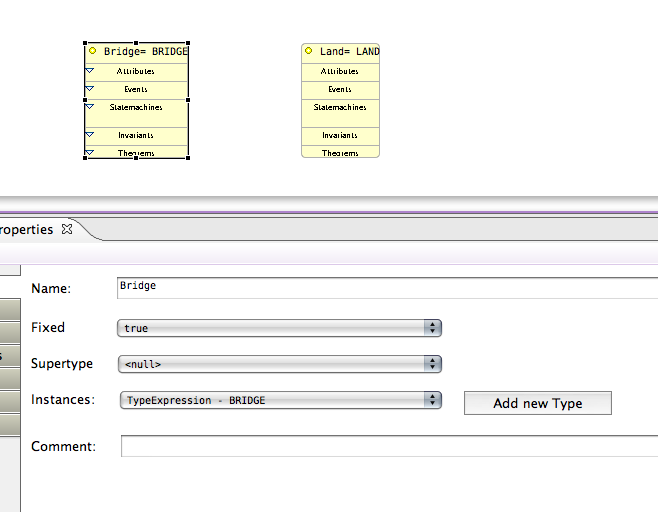
In order to use these concepts in a class diagram (i.e. to add variables and events based on this configuration data) I would add corresponding classes and set their variability to fixed (because we don't want to model creation of land and bridges). To force them to have the same instances as the class types I add a new type expression for each class type, BRIDGE and LAND, and then set the corresponding class instances to these types. (Note that using supertype would make the class instances into subsets of the configuration data which is not quite what we want here).
Of course, for this example, you could obtain a much simpler model by leaving out the explicit modelling of bridge, island and mainland, but the advantage of our model is that it can easily be extended to deal with different configurations having several bridges and islands.