Talk:Event-B Language: Difference between revisions
imported>Son →What do you mean by "cannot be parsed"?: new section |
imported>Jens |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
The problems is as follows. | The problems is as follows. | ||
I build one project, in which there is only one context. In this contest, there is only one theorem defined as {x·x∈0‥4∣x↦0}∈0‥4⇸0‥4. The obligation for it is generated by Rodin. However, it reports that the obligation | I build one project, in which there is only one context. In this contest, there is only one theorem defined as {x·x∈0‥4∣x↦0}∈0‥4⇸0‥4. The obligation for it is generated by Rodin. However, it reports that the obligation cannot be passed. It makes me quite confused. Please everyone knowing what the problem is and help me out. | ||
Thank you so lot | Thank you so lot | ||
| Line 18: | Line 18: | ||
Son | Son | ||
== It is not "parsed" but "passed" == | |||
Much appreciation for that reply. Thanks. | |||
It means that the oblligation for this theorem is listed but remained red. The screen snapshot is | |||
"http://4.bp.blogspot.com/_GexLXHeTL7w/Sub0Xb8WoII/AAAAAAAAAD4/5u5XGKlTBTY/s1600/ebp.jpg" | |||
Futhermore, I have installed the newest version of Rodin (rodin-1.1RC1). I put "{x·x∈0‥4∣x↦0}∈0‥4⇸0‥4" in the AXIOMS and tick it as a theorem. However, the problem is the same as Rodin 0.9.1. | |||
== Have you installed the provers ?== | |||
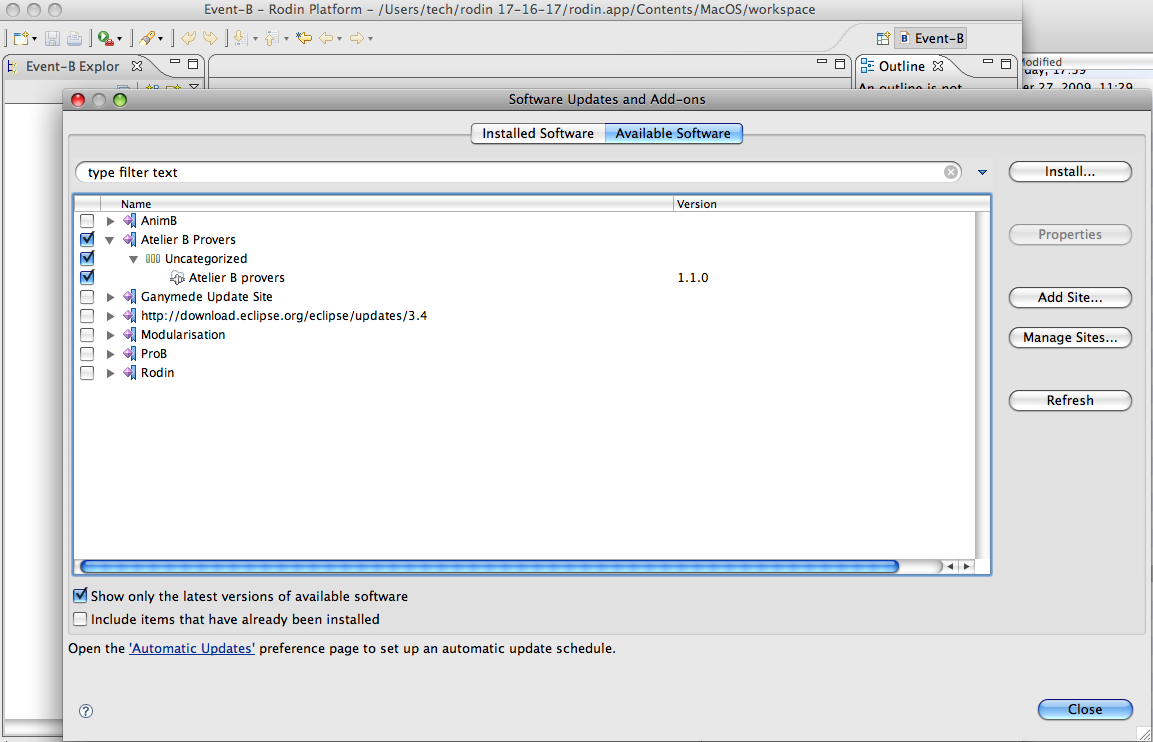
For legal reasons, Rodin does not contain the Atelier B Provers. You need to install them separately using the update site | |||
If you have the provers installed, you can prove the theorem by clicking on the second ∈ in the goal and afterwards use ML. | |||
Cheers | |||
Jens | |||
[[Image:HaiYun prove.png]] | |||
[[Image:Install_Provers.png]] | |||
Latest revision as of 21:22, 30 October 2009
Rodin Platform Version: 0.9.1
Sequent Prover Auto-tactic : all
The problems is as follows. I build one project, in which there is only one context. In this contest, there is only one theorem defined as {x·x∈0‥4∣x↦0}∈0‥4⇸0‥4. The obligation for it is generated by Rodin. However, it reports that the obligation cannot be passed. It makes me quite confused. Please everyone knowing what the problem is and help me out.
Thank you so lot
HaiYun tian SCM Teesside University
What do you mean by "cannot be parsed"?
I am a bit confused with the "obligation cannot be parsed". I tried to enter this in Rodin (1.1) and there is not such problem. It cannot be automatic proved though.
Cheers,
Son
It is not "parsed" but "passed"
Much appreciation for that reply. Thanks. It means that the oblligation for this theorem is listed but remained red. The screen snapshot is "http://4.bp.blogspot.com/_GexLXHeTL7w/Sub0Xb8WoII/AAAAAAAAAD4/5u5XGKlTBTY/s1600/ebp.jpg"
Futhermore, I have installed the newest version of Rodin (rodin-1.1RC1). I put "{x·x∈0‥4∣x↦0}∈0‥4⇸0‥4" in the AXIOMS and tick it as a theorem. However, the problem is the same as Rodin 0.9.1.
Have you installed the provers ?
For legal reasons, Rodin does not contain the Atelier B Provers. You need to install them separately using the update site
If you have the provers installed, you can prove the theorem by clicking on the second ∈ in the goal and afterwards use ML.
Cheers
Jens