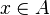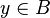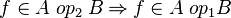Maplet Overriding in Goal: Difference between revisions
imported>Billaude |
imported>Laurent mNo edit summary |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
= Objective = | = Objective = | ||
Split every goal in the form : <math>f\ovl{\{x\mapsto y\}}\in A\ | Split every goal in the form : <math>f\ovl{\{x\mapsto y\}}\in A\;op_1\;B </math> into two sub-goals if and only if the sequent contains a hypothesis such as <math>f\in A\;op_2\;B</math> : | ||
:*<math>x\in A</math> | :*<math>x\in A</math> | ||
:*<math>y\in B</math> | :*<math>y\in B</math> | ||
Where <math> | Where <math>op_1</math> denote either a Relation <math>\left(\rel\right)</math>, or a Total Relation <math>\left(\trel\right)</math>, or a Partial Function <math>\left(\pfun\right)</math>, or a Total Function <math>\left(\tfun\right)</math>, and <math>op_2</math> is such as <math>f\in A\;op_2\;B\limp f\in A\;op_1\;B</math>. | ||
= Design Decision = | = Design Decision = | ||
Those | Those two subgoals and the predicate are not equivalent to the goal. Indeed, in the case <math>op_1</math> is a Relation, the goal is equivalent to <math>\{x\}\domsub f\in A\setminus\{x\}\rel B\land x\in A\land y\in B</math>. But this has the drawback of writing three times the expression ''x''. If this expression is big, then it can make the proof rule hard to read. | ||
But, we know that <math>\left(f\in A\; | But, we know that <math>\left(f\in A\;op_1\;B\right)\limp \left(\{x\}\domsub f\in A\setminus\{x\}\;op_1\;B\right)</math> for all the relation given in Objective. By ensuring that <math>f\in A\;op_2\;B</math> is among the hypotheses of the sequent, we ensure that the first predicate of the conjunction is provable. Indeed, if this check was not done, the proof obligation may be unprovable since there are a loss of informations by writing <math>f\in A\;op_2\;B</math> instead of <math>\{x\}\domsub f\in A\setminus\{x\}\;op_1\;B</math>. | ||
= Table = | |||
{| class="wikitable alternance" style="text-align:center; width:80%;" | |||
|+ <math>f\in A\;op_2\;B\limp f\in A\;op_1 B</math> | |||
|- | |||
|<math>op_1\;\backslash\;op_2</math> | |||
! scope=col | <math>\rel</math> | |||
! scope=col | <math>\trel</math> | |||
! scope=col | <math>\srel</math> | |||
! scope=col | <math>\strel</math> | |||
! scope=col | <math>\pfun</math> | |||
! scope=col | <math>\tfun</math> | |||
! scope=col | <math>\pinj</math> | |||
! scope=col | <math>\tinj</math> | |||
! scope=col | <math>\psur</math> | |||
! scope=col | <math>\tsur</math> | |||
! scope=col | <math>\tbij</math> | |||
|- | |||
! scope=row | <math>\rel</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\trel</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\srel</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\strel</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\pfun</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\tfun</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\pinj</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\tinj</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\psur</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\tsur</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|<math>\checkmark</math> | |||
|- | |||
! scope=row | <math>\tbij</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>-</math> | |||
|<math>\checkmark</math> | |||
|- | |||
|} | |||
[[Category:Design | |||
[[Category:Design]] | |||
Latest revision as of 16:05, 18 March 2014
This page describes the design of a tactic requested here : Feature Request #3306228
Objective
Split every goal in the form : 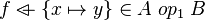 into two sub-goals if and only if the sequent contains a hypothesis such as
into two sub-goals if and only if the sequent contains a hypothesis such as 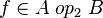 :
:
Where 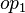 denote either a Relation
denote either a Relation 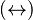 , or a Total Relation
, or a Total Relation 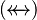 , or a Partial Function
, or a Partial Function 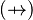 , or a Total Function
, or a Total Function 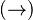 , and
, and 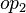 is such as
is such as 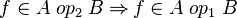 .
.
Design Decision
Those two subgoals and the predicate are not equivalent to the goal. Indeed, in the case 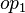 is a Relation, the goal is equivalent to
is a Relation, the goal is equivalent to 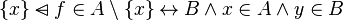 . But this has the drawback of writing three times the expression x. If this expression is big, then it can make the proof rule hard to read.
. But this has the drawback of writing three times the expression x. If this expression is big, then it can make the proof rule hard to read.
But, we know that 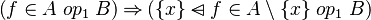 for all the relation given in Objective. By ensuring that
for all the relation given in Objective. By ensuring that 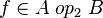 is among the hypotheses of the sequent, we ensure that the first predicate of the conjunction is provable. Indeed, if this check was not done, the proof obligation may be unprovable since there are a loss of informations by writing
is among the hypotheses of the sequent, we ensure that the first predicate of the conjunction is provable. Indeed, if this check was not done, the proof obligation may be unprovable since there are a loss of informations by writing 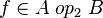 instead of
instead of 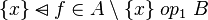 .
.
Table
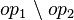
|
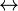
|
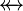
|
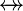
|
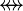
|
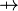
|
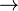
|
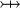
|
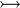
|
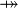
|
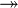
|
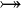
|
|---|---|---|---|---|---|---|---|---|---|---|---|
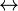
|

|

|

|

|

|

|

|

|

|

|

|
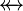
|

|

|

|

|

|

|

|

|

|

|

|
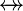
|

|

|

|

|

|

|

|

|

|

|

|
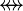
|

|

|

|

|

|

|

|

|

|

|

|
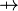
|

|

|

|

|

|

|

|

|

|

|

|
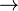
|

|

|

|

|

|

|

|

|

|

|

|
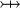
|

|

|

|

|

|

|

|

|

|

|

|
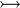
|

|

|

|

|

|

|

|

|

|

|

|
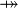
|

|

|

|

|

|

|

|

|

|

|

|
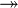
|

|

|

|

|

|

|

|

|

|

|

|
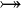
|

|

|

|

|

|

|

|

|

|

|

|