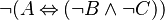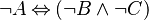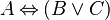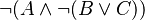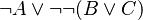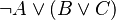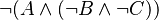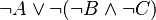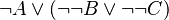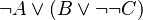Negation Normal Form: Difference between revisions
imported>Laurent |
imported>Laurent Fully edited explanations and examples |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
This page | This page describes the design of a tactic for putting a sequent in Negation Normal Form, as requested by | ||
[https://sourceforge.net/tracker/index.php?func=detail&aid=3137893&group_id=108850&atid=651672 Feature Request #3137893]. | |||
= | = Objective = | ||
A | A predicate is in Negation Normal Form when negation occurs only on atomic expression. To compute such a normal form, the following rewrite rules (which are already implemented in Rodin) are used: | ||
:SIMP_NOT_NOT: <math> \lnot\, \lnot\, P \;\;\defi\;\; P </math> | |||
:DISTRI_NOT_AND: <math> \lnot\,(P \land Q) \;\;\defi\;\; \lnot\, P \lor \lnot\, Q </math> | |||
:DISTRI_NOT_OR: <math> \lnot\,(P \lor Q) \;\;\defi\;\; \lnot\, P \land \lnot\, Q </math> | |||
:DERIV_NOT_IMP: <math> \lnot\,(P \limp Q) \;\;\defi\;\; P \land \lnot\, Q </math> | |||
:DERIV_NOT_FORALL: <math> \lnot\, \forall x \qdot P \;\;\defi\;\; \exists x \qdot \lnot\, P </math> | |||
:DERIV_NOT_EXISTS: <math> \lnot\, \exists x \qdot P \;\;\defi\;\; \forall x \qdot \lnot\, P </math> | |||
However, no rule has been defined for the case where the inner predicate is an equivalence, such as <math> \lnot (P \leqv Q) </math>, which is equivalent to both <math> \lnot P \leqv Q</math> and <math>P \leqv\lnot Q</math>. Currently, the tactic will not do anything for such predicates. | |||
= Analysis = | |||
For equivalence predicate, as the tactic is to be designed for interactive use, we prefer to keep the equivalence predicate (rather than translate it to e.g., double implication). However, it is not clear how to decide which sub-predicate should get the negation. Some cases seem obvious. For instance, if one of the child is itself a negation, it seems a good idea to push the negation to this child (where both negations will cancel each other). Similarly, if one child is atomic, pushing the negation to this child seems also a good candidate. | |||
However, in the general case, it is not easy to decide to which child the negation shall be pushed downto. For instance, consider predicate | |||
:<math>\lnot(A \leqv (\lnot B \land\lnot C))</math> | |||
If we push negation to the left-hand child, we obtain the equivalent predicate | |||
:<math>\lnot A \leqv (\lnot B \land\lnot C)</math> | |||
But, if we push it to the right-hand child, we get the normal form | |||
:<math> A \leqv (B \or C)</math> | |||
which is highly preferable, as it is simpler to read. | |||
It is not yet clear whether there is a good criterion for deciding which child to go for. | |||
= Implementation = | = Implementation = | ||
The tactic shall apply to all visible hypotheses and the goal of a sequent. It should apply repeatedly the above rewrite rules until all these predicates are in Negation Normal Form. | |||
However, care should be taken when organising the applications of these rules. They should be applied following a pre-order traversal of the predicate, to avoid undoing and redoing several times the same operations. This can be easily shown in the following example. | |||
<math>\lnot A \lor (B \lor C)</math> | When rewrite rules are applied in the right order, the following rewrites are performed | ||
:<math>\lnot(A \land \lnot (B \lor C))</math> | |||
:<math>\lnot A \lor \lnot\lnot (B \lor C)</math> | |||
:<math>\lnot A \lor (B \lor C)</math> | |||
However, if another order is used, one could get a much longer rewriting chain, such as | |||
:<math>\lnot(A \land \lnot (B \lor C))</math> | |||
:<math>\lnot(A \land (\lnot B \land \lnot C))</math> | |||
:<math>\lnot A \lor \lnot(\lnot B \land \lnot C)</math> | |||
:<math>\lnot A \lor (\lnot\lnot B \lor \lnot\lnot C)</math> | |||
:<math>\lnot A \lor (B \lor \lnot\lnot C)</math> | |||
:<math>\lnot A \lor (B \lor C)</math> | |||
Latest revision as of 16:48, 13 April 2011
This page describes the design of a tactic for putting a sequent in Negation Normal Form, as requested by Feature Request #3137893.
Objective
A predicate is in Negation Normal Form when negation occurs only on atomic expression. To compute such a normal form, the following rewrite rules (which are already implemented in Rodin) are used:
- SIMP_NOT_NOT:

- DISTRI_NOT_AND:
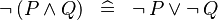
- DISTRI_NOT_OR:
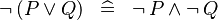
- DERIV_NOT_IMP:
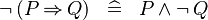
- DERIV_NOT_FORALL:
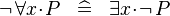
- DERIV_NOT_EXISTS:
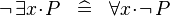
However, no rule has been defined for the case where the inner predicate is an equivalence, such as 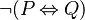 , which is equivalent to both
, which is equivalent to both 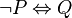 and
and 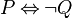 . Currently, the tactic will not do anything for such predicates.
. Currently, the tactic will not do anything for such predicates.
Analysis
For equivalence predicate, as the tactic is to be designed for interactive use, we prefer to keep the equivalence predicate (rather than translate it to e.g., double implication). However, it is not clear how to decide which sub-predicate should get the negation. Some cases seem obvious. For instance, if one of the child is itself a negation, it seems a good idea to push the negation to this child (where both negations will cancel each other). Similarly, if one child is atomic, pushing the negation to this child seems also a good candidate.
However, in the general case, it is not easy to decide to which child the negation shall be pushed downto. For instance, consider predicate
If we push negation to the left-hand child, we obtain the equivalent predicate
But, if we push it to the right-hand child, we get the normal form
which is highly preferable, as it is simpler to read.
It is not yet clear whether there is a good criterion for deciding which child to go for.
Implementation
The tactic shall apply to all visible hypotheses and the goal of a sequent. It should apply repeatedly the above rewrite rules until all these predicates are in Negation Normal Form.
However, care should be taken when organising the applications of these rules. They should be applied following a pre-order traversal of the predicate, to avoid undoing and redoing several times the same operations. This can be easily shown in the following example.
When rewrite rules are applied in the right order, the following rewrites are performed
However, if another order is used, one could get a much longer rewriting chain, such as