|
|
| (19 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| This page is under development. | | This page is under development. It is intended to be a user oriented manual for using records in Event-B. This page should be read in conjunction with the [[Structured_Types|Structured Types]] page which gives a more theoretical description of the origin of the Records extension. |
| | |
| It is intended to be a user oriented manual for using records in Event-B. This page is derived from the [[Structured_Types|Structured Types]] page which gives a more theoretical description of the origin of the Records extension. | |
|
| |
|
| ==Introduction== | | ==Introduction== |
| Line 7: |
Line 5: |
| The Records Extension introduces a new modelling construct to provide a notion of structured types in Event-B Contexts. | | The Records Extension introduces a new modelling construct to provide a notion of structured types in Event-B Contexts. |
|
| |
|
| Currently, structured variables are not supported. Variables that are typed as an instance of a record type can be thought of as identifying a particular record value. Hence it is not possible to vary an individual field, the variable must be assigned a complete new record value instance. To vary an individual field this new record value instance can be selected to have the same field value for every other field.)
| | Currently, structured variables are not supported. Variables that are typed as an instance of a record type can be thought of as identifying a particular record value. Hence it is not possible to vary an individual field, the variable must be assigned a complete new record value instance. To vary an individual field this new record value instance can be selected to have the same field value for every other field.) |
|
| |
|
| ==UI Extensions== | | ==UI Extensions== |
| The '''Event-B editor''' is extended to include two new top level clauses. These are '''Record Declarations''' and '''Record Extensions'''. | | The '''Event-B editor''' is extended to include two new top level clauses. These are '''Record Declarations''' and '''Record Extensions'''. |
|
| |
|
| Records (or sub-records) are introduced in the Record Declarations clause. Records that are introduced here without a '''Supertypes''' clause are equivalent to carrier sets. Those that have a Supertypes clause are equivalent to constants that are a subset of the referenced (i.e. subtyped) record. | | Records (or sub-records) are introduced in the Record Declarations clause. Records that are introduced here without a '''Supertypes''' clause are equivalent to carrier sets. Those that have a Supertypes clause are equivalent to constants that are a subset of the referenced (i.e. subtyped) record or carrier set. |
|
| |
|
| Record Extensions may only add new fields to a record that has previously been declared in a Record Declaration. The extended record is referenced in an 'extends' clause. | | Record Extensions may only add new fields to a record that has previously been declared in a Record Declaration. The extended record is referenced in an 'extends' clause. |
| | |
| | Record Declaration clause also contains a toggle button to control the record's closure property. A closed record cannot be subtyped by other records or extended by record extensions. |
|
| |
|
| The '''Event-B navigator''' is extended to show a new node '''Records'''. Under this node are listed the records and records extensions in the Context. | | The '''Event-B navigator''' is extended to show a new node '''Records'''. Under this node are listed the records and records extensions in the Context. |
| Line 27: |
Line 27: |
| The semantics of Records are given by their translation into 'pure' Event-B. This translation is performed by extensions to the static checker which generates a 'checked context' (.BCC file) containing pure Event-B from an unchecked (.BUC file) containing record elements. Hence the translated Event-B is not visible to the user. | | The semantics of Records are given by their translation into 'pure' Event-B. This translation is performed by extensions to the static checker which generates a 'checked context' (.BCC file) containing pure Event-B from an unchecked (.BUC file) containing record elements. Hence the translated Event-B is not visible to the user. |
|
| |
|
| <formatting/presentation of this will be improved>
| |
|
| |
| Record R Extends <null> --> Carrier Set R
| |
|
| |
| Record S Extends R --> Constant S, Axiom S : POW(R)
| |
|
| |
| field f : F --> Constant f, Axiom f : R >-> F
| |
|
| |
| ==Copy of the original Structured Types wiki page from which this page is currently being derived <This will be removed> ==
| |
|
| |
| The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures.
| |
| Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes. For example,
| |
| suppose we wish to model a record structure ''R'' with fields ''e'' and ''f'' (with type ''E'' and ''F'' respectively).
| |
| Let us use the following 'invented' syntax for this (based on VDM syntax but currently not part of Event-B syntax):
| |
|
| |
|
| <center> | | <center> |
| {{SimpleHeader}} | | {| align="centre" border = "1" cellpadding = "10" cellspacing="5" |
| |<math> \begin{array}{lcl} | | |<math> \textbf{ RECORD}~~~~ R </math> || <math> \textbf{~~SET}~~~~ R </math> |
| \textbf{RECORD}~~~~ R &::& e\in E\\ | | |- |
| && f \in F
| | |<math> \textbf{ RECORD}~~~~ R, ~~~~\textbf{SUPERTYPE}~~~~ S ~~~~</math> || <math> \textbf{~~CONSTANT}~~~~ R , ~~~~\textbf{AXIOM}~~~~ R \in \pow (S) ~~~~</math> |
| \end{array} | | |- |
| </math> | | |<math> \textbf{ FIELD}~~~~ f \in F</math> || <math> \textbf{~~CONSTANT}~~~~ f , ~~~~\textbf{AXIOM}~~~~ f \in R \rightarrow F ~~~~</math> |
| |} | | |} |
| </center> | | </center> |
|
| |
|
| We can model this structure in Event-B by introducing (in a context) a carrier set ''R'' and two
| |
| functions ''e'' and ''f'' as constants as follows:
| |
|
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{SETS}~~ R\\
| |
| \textbf{CONSTANTS}~~ e,~ f\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| e \in R \tfun E\\
| |
| f \in R \tfun F\\
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
|
| |
|
| |
| The (constant) functions ''e'' and ''f'' are ''projection'' functions that can be used to extract the appropriate field values.
| |
| That is, given an element <math>r\in R</math> representing a record structure, we write <math>e(r)</math> for the ''e'' component of ''r'' and <math>f(r)</math> for the ''f'' component of ''r''.
| |
|
| |
| ''E'' and ''F'' can be any type definable in Event-B, including a type representing a record structure.
| |
|
| |
| The approach to modelling structured types is based on a proposal by Evans and Butler
| |
| [http://eprints.ecs.soton.ac.uk/12024/].
| |
| We refer to this approach to modelling records as a ''projection-based'' approach.
| |
| Later we will look at a ''constructor-based'' approach and make the link between the two approaches.
| |
|
| |
|
| |
| ==Constructing Structured Values==
| |
|
| |
| Suppose we have a variable ''v'' in a machine whose type is the structure ''R'' defined above:
| |
|
| |
| <center>
| |
| <math>\textbf{INVARIANT}~~ v\in R</math>
| |
| </center>
| |
|
| |
| We wish to assign a structured value to ''v'' whose ''e'' field has some value ''e1'' and whose ''f'' field has some value ''f1''.
| |
| This can be achieved by specifying the choice of an event parameter ''r'' whose fields are constrained by appropriate guards
| |
| and assigning parameter ''r'' to the machine variable ''v''. This is shown in the following event:
| |
|
| |
|
| <center><math>
| | [It may be instructive to open the *.bcc file with a text editor to examine the generated carrier sets, constants, and axioms] |
| Ev1 ~=\begin{array}[t]{l}
| |
| \textbf{ANY}~~ r ~~\textbf{WHERE} \\
| |
| ~~~~ r \in R \\
| |
| ~~~~ e( r ) = e1 \\
| |
| ~~~~ f( r ) = f1 \\
| |
| \textbf{THEN} \\
| |
| ~~~~ v := r \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
|
| |
|
| If we only wish to update some fields and leave others changed, this needs to be done by specifying explicitly that some fields
| | ==Usage== |
| remain unchanged. This is shown in the following example where only the ''e'' field is modified:
| |
|
| |
|
| <center><math> | | First define Records in the Record Declarations section. Some of these can subtype others but you need at least one that is not a subset, i.e. has no supertypes. <s>Note that we decided not to allow records to subtype or extend Carrier Sets, but you can do the equivalent by defining a record without any fields and subtyping/extending that.</s> To be correctly static-checked record definitions must be in order of their referencing i.e. a subtype record would follow a supertype record which it references (to know about its type). In opposite case static checker will show a typing problem. |
| Ev2 ~=\begin{array}[t]{l}
| |
| \textbf{ANY}~~ r ~~\textbf{WHERE} \\
| |
| ~~~~ r \in R \\
| |
| ~~~~ e( r ) = e1 \\
| |
| ~~~~ f( r ) = f(v) \\
| |
| \textbf{THEN} \\
| |
| ~~~~ v := r \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
|
| |
|
| If we don't care about the value of some field (e.g., ''f''), we simply omit any guard on that field as follows:
| | Add fields and give them a type by entering an expression that evaluates to a set. Note that this expression must be a basic type expression. You can use records, constants and sets in the expression. |
|
| |
|
| <center><math>
| | After a record is defined it can be declared as closed using a toggle button in its Record Declaration clause. When record is closed it cannot be subtyped or extended anymore. Another effect of closing a record is that additional axioms are generated for it in the checked context. These include a closure axiom, a make-function for the record and an update-function for each of its fields (also for derived fields from supertype records). Another axiom — feasibility axiom — is generated for every record independent of its closure attribute. |
| Ev3 ~= \begin{array}[t]{l}
| |
| \textbf{ANY}~~ r ~~\textbf{WHERE} \\
| |
| ~~~~ r \in R \\
| |
| ~~~~ e( r ) = e1 \\
| |
| \textbf{THEN} \\
| |
| ~~~~ v := r \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
|
| |
|
| | For Record Extensions just select the record you want to add new fields to from the drop down list and then add the new fields. Only open (not closed) records can be extended, although the drop down list contains all the declared records. |
|
| |
|
| Sometimes we will wish to model a set of structured elements as a machine variable, e.g.,
| | You can refer to records and fields in axioms/theorems. E.g., you could define a constant to be an instance of a record. In all cases you can refer to records and fields in the current or visible abstract (extended*) contexts. |
|
| |
|
| <center>
| | You use fields as if they were functions (which is what they are in the checked context). |
| <math>\textbf{INVARIANT}~~ vs\subseteq R</math>
| |
| </center>
| |
|
| |
|
| We can add a structured element to this set using the following event:
| | e.g. if <math>r</math> belongs to <math>myRecord</math> which has a field, <math>myField \in \nat</math> then I could write in a predicate <math> myField(r) > 5 </math>. |
|
| |
|
| <center><math>
| | ==Proving With Records== |
| AddElement ~=
| | The prover will refer to records as sets and constants, and to fields as constants. Therefore for proving you may need to be aware of this. |
| \begin{array}[t]{l}
| |
| \textbf{ANY}~~ r ~~\textbf{WHERE} \\
| |
| ~~~~ r \in R \\
| |
| ~~~~ e( r ) = e1 \\
| |
| ~~~~ f( r ) = f1 \\
| |
| \textbf{THEN} \\
| |
| ~~~~ vs := vs \cup \{r\} \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
|
| |
|
| ==Extending Structured Types==
| | Axioms that are automatically generated for typing records and their fields will have automatically generated labels and these may be referenced in the prover interface. |
|
| |
|
| In a refinement we can introduce new fields to an existing structured type. Suppose R is defined in context C1
| | The automatically generated labels use an easy to interpret format: |
| with fields ''e'' and ''f'' as before.
| | * Subtype Record typing axioms are in the format ''<recordName>.type<d>'' (where d is a decimal digit appended to ensure there are no name clashes) |
| For the refinement, suppose we wish to add a field ''g'' of type ''G'' to structured type ''R''.
| | * Field typing axioms are in the format ''<recordName>.<fieldName>.type<d>'' (where d is a decimal digit appended to ensure there are no name clashes) |
| Let us use the following invented syntax for this (not part of Event-B syntax):
| |
|
| |
|
| <center>
| | Other axioms use record and field labels in their labelling, which leads to a longer and slightly confusing but still interpretable format: |
| {{SimpleHeader}}
| | * Feasibility axioms are in the format ''<recordName>.feasibility'' (or ''<recordName>.feasibility.ext<n>'' in case of record extensions) |
| |<math> \begin{array}{l}
| | * Closure axioms are in the format ''<recordName>.closure'' |
| \textbf{EXTEND~~ RECORD}~~ R ~~\textbf{WITH}~~ g\in G
| | * Make function's 1st axiom (function's typing) is in the format ''<recordName>.make.axm1'' |
| \end{array}
| | * Make function's 2nd axiom (for each field) is in the format ''<recordName>.<fieldName>.make.axm2'' |
| </math>
| | * Update function's 1st axiom (record field update function's typing) is in the format ''<recordName>.<fieldName>.update.axm1'' |
| |}
| | * Update function's 2nd axiom (equivalence to record construction with a specific value of updated field) is in the format ''<recordName>.<fieldName>.update.axm2'' |
| </center>
| |
| | |
| This can be done by including the new field ''g'' as projection function on ''R'' in a context ''C2'' (that extends ''C1'').
| |
| The new field is defined as follows:
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{CONSTANTS}~~ g \\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| g \in R \tfun G \\
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| Above, we saw the ''AddElement'' event that adds a structured element to the set ''vs''.
| |
| We may want to specify a value for the new ''g'' field in the refinement of this event.
| |
| Using the event extension mechanism, this can be achieved as follows:
| |
| <center><math>
| |
| AddElement~= \begin{array}[t]{l}
| |
| \textbf{EXTENDS}~~ AddElement \\
| |
| \textbf{WHEN} \\
| |
| ~~~~ g( r ) = g1 \\
| |
| \textbf{THEN} \\
| |
| ~~~~ skip \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
| | |
| This is a form of superposition refinement where we add more data structure to the state by
| |
| adding a new field to elements of the structured type ''R''. In the above event we strengthen
| |
| the specification by adding a guard using the event extension mechanism.
| |
| The event extension mechanism means that this short form is the same as specifying
| |
| the refined event as follows:
| |
| <center><math>
| |
| AddElement ~=
| |
| \begin{array}[t]{l}
| |
| \textbf{REFINES}~~ AddElement \\
| |
| \textbf{ANY}~~ r ~~\textbf{WHERE} \\
| |
| ~~~~ r \in R \\
| |
| ~~~~ e( r ) = e1 \\
| |
| ~~~~ f( r ) = f1 \\
| |
| ~~~~ g( r ) = g1 \\
| |
| \textbf{THEN} \\
| |
| ~~~~ vs := vs \cup \{r\} \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
| | |
| ==Sub-Typing==
| |
| | |
| Extension, as described above, is used when adding new fields to a structured type as part of a refinement step.
| |
| That is, at different abstraction levels, we may have different numbers of fields in a structured type.
| |
| | |
| Sometimes we wish to have different subtypes of a structure at the ''same'' abstraction level.
| |
| We can achieve this by defining subsets of the structure type and defining projection functions for those
| |
| subsets only. For example suppose we define a message type that has ''sender'' and ''receiver'' fields as well
| |
| as a message ''identifier''.
| |
| In our invented notation this would be:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{lcl}
| |
| \textbf{RECORD}~~~~ Message &::& sender\in Agent\\
| |
| && receiver \in Agent \\
| |
| && ident \in Ident
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| In Event-B this would be:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{SETS}~~ Message\\
| |
| \textbf{CONSTANTS}~~ sender,~ receiver, ident\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| sender \in Message \tfun Agent\\
| |
| receiver \in Message \tfun Agent\\
| |
| ident \in Message \tfun Ident
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| We wish to have two subtypes of message, ''request'' messages and ''confirmation'' messages.
| |
| We define two subsets of ''Message'' as follows:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{CONSTANTS}~~ \textit{ReqMessage},~ \textit{ConfMessage}\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| \textit{ReqMessage} \subseteq Message \\
| |
| \textit{ConfMessage} \subseteq Message \\
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| | |
| We require requests to have a product and an amount field and a confirmation to have a price field.
| |
| In our invented notation this would be specified as follows:
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{EXTEND~~ RECORD}~~ \textit{ReqMessage}~~\textbf{WITH}\\
| |
| ~~~~~~~~~~~~ product\in Product\\
| |
| ~~~~~~~~~~~~ amount\in \nat\\
| |
| \textbf{EXTEND~~ RECORD}~~ \textit{ConfMessage}~~\textbf{WITH}\\
| |
| ~~~~~~~~~~~~ price\in \nat\\ \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| In Event-B the additional fields are specified as projection functions on the relevant message subsets:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{CONSTANTS}~~ product,~ amount,~ price\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| product \in \textit{ReqMessage} \tfun Product\\
| |
| amount \in \textit{ReqMessage} \tfun \nat\\ ~\\
| |
| price \in \textit{ConfMessage} \tfun \nat
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| Typically we would require that the message subtypes are disjoint. In that case we would add an additional axiom:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| \textit{ReqMessage} \cap \textit{ConfMessage} ~=~ \emptyset \\
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| If we know that there are no other subtypes besides requests and confirmations and that they should be disjoint,
| |
| then we can condense the subset and disjointness axioms into a partitions axiom:
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| partition(~ Message, ~\textit{ReqMessage},~ \textit{ConfMessage} ~)
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| | |
| Suppose we have 2 variables representing request and confirmation channels repsectively:
| |
| | |
| <center>
| |
| <math>
| |
| \begin{array}{l}
| |
| \textbf{INVARIANT}~~ \\
| |
| ~~~~req\_channel \subseteq \textit{ReqMessage} \\
| |
| ~~~~\textit{conf\_channel} \subseteq \textit{ConfMessage}
| |
| \end{array}
| |
| </math>
| |
| </center>
| |
| | |
| The following ''Confirm'' event models an agent responding to request by issuing a confirmation message.
| |
| The ''Confirm'' event is enabled for the agent if there is a request message, ''req'', whose receiver is that agent.
| |
| The effect of the event is to chose a confirmation message, ''conf'', whose fields are constrained with appropriate guards and add that confirmation message to the confirmations channel:
| |
| | |
| <center><math>
| |
| Confirm ~=
| |
| \begin{array}[t]{l}
| |
| \textbf{ANY}~~ req,~ conf, ~ agent ~~\textbf{WHERE} \\
| |
| ~~~~ req \in req\_channel \\
| |
| ~~~~ agent = receiver(req) \\
| |
| ~~~~ conf \in \textit{ConfMessage} \\
| |
| ~~~~ sender( conf ) = agent \\
| |
| ~~~~ receiver( conf ) = sender(req) \\
| |
| ~~~~ price(conf) = calculate\_price(~ product(req)\mapsto amount(req) ~) \\
| |
| \textbf{THEN} \\
| |
| ~~~~ \textit{conf\_channel} := \textit{conf\_channel} \cup \{conf\} \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
| | |
| | |
| It might seem that we should always specify that subtypes are disjoint, but this is not so.
| |
| Not making them disjoint allows us to represent a form of 'mulitple inheritance'.
| |
| For example, we could declare a new subtype ''ReqConfMessage'' that subsets both
| |
| ''ReqMessage'' and ''ConfMessage'':
| |
| <center> | |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{CONSTANTS}~~ \textit{ReqConfMessage},\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| \textit{ReqConfMessage} \subseteq \textit{ReqMessage} \\
| |
| \textit{ReqConfMessage} \subseteq \textit{ConfMessage} \\
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| Elements of ''ReqConfMessage'' will have the fields of both subtypes, i.e.,
| |
| ''sender'', ''receiver'', ''ident'', ''product'', ''amount'' and ''price''. | |
| | |
| This combined subtype could be further extended:
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{EXTEND~~ RECORD}~~ \textit{ReqConfMessage}~~\textbf{WITH}\\
| |
| ~~~~~~~~~~~~ time\in TIME\\ \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| | |
| | |
| For an example of a Rodin development that uses the projection-based approach to modelling and extending records see [http://deploy-eprints.ecs.soton.ac.uk/9/]
| |
| | |
| ==Constructor-based Records==
| |
| | |
| An alternative style of modelling records is to define constructor functions that
| |
| construct a record from a tuple of the components of that record.
| |
| This is the approach that VDM follows, for example.
| |
| Suppose we wish to model the following record structure:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{lcl}
| |
| \textbf{RECORD}~~~~ R &::& e\in E\\
| |
| && f \in F
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| We introduce the constructor function for ''R'' records, ''mk-R'', as follows:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{SETS}~~ R\\
| |
| \textbf{CONSTANTS}~~ \textit{mk-R},~ e,~ f\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| \textit{mk-R} ~\in~ (E\times F) \tbij R\\
| |
| e \in R \tfun E\\
| |
| f \in R \tfun F\\
| |
| \forall x,y \cdot e( \textit{mk-R}(x\mapsto y) ) = x \\
| |
| \forall x,y \cdot f( \textit{mk-R}(x\mapsto y) ) = y
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| The ''mk-R'' function is specified as a constructor for type ''R'' that takes an element of type ''E'' and an element of type ''F''
| |
| and constructs an value of type ''R''.
| |
| The constructor is specified as injective because when the components are different, then the corresponding records should be different.
| |
| The above declaration also makes the constructor surjective which means that the constructor provides a way of generating all
| |
| records of type ''R''.
| |
| | |
| With the constructor based approach, the ''AddElement'' event already shown above does not require a selection of a
| |
| record satisfying the required properties. Instead we use the constructor directly:
| |
| | |
| <center><math>
| |
| AddElement ~=
| |
| \begin{array}[t]{l}
| |
| \textbf{BEGIN}\\
| |
| ~~~~ vs := vs \cup \{~ \textit{mk-R}(e1,f1) ~\} \\
| |
| \textbf{END}
| |
| \end{array}
| |
| </math></center>
| |
| | |
| It is possible to define different subtypes in a similar way as in the projection-based approach by defining separate constructors for
| |
| each (disjoint) subtype. | |
| | |
| Adding new fields in a refinement is more difficult with the constructor approach however.
| |
| We would need to introduce a completely new constructor for the full extended record structure and
| |
| to get the refinement to work correctly, we would need to define a relationship between the original
| |
| record and the extended version. This merits further exploration.
| |
| | |
| ==Projections versus Constructors==
| |
| | |
| As we have seen, the constructor approach can lead to more succinct event specifications
| |
| than the projection approach.
| |
| The downside of the constructor approach is that it is difficult to extend records in refinement steps and
| |
| stepwise refinement and introduction of structure through refinement is an major feature of the
| |
| Event-B approach.
| |
| | |
| We could say that the projection approach gives us ''open'' record structures, that is,
| |
| structures that are easy to extend in a refinement. The constructor approach gives us
| |
| ''closed'' records that are not directly extendable in refinement steps.
| |
| | |
| The constructor approach can be seen as a strengtening of the projection approach
| |
| as is now explained. Consider again the two projection functions introduced to
| |
| represent fields of the record structure ''R'' in the projection approach:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| e \in R \tfun E\\
| |
| f \in R \tfun F
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| The direct product of these two projections <math>(e \otimes f)</math> has the following type:
| |
| | |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| ~~~~\begin{array}{l}
| |
| e \otimes f ~\in~ R \tfun (E\times F)
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
| | |
| The inverse of the direct product
| |
| <math>(e \otimes f)^{-1}</math> relates pairs of type <math>E\times F</math> to elements of type <math>R</math>.
| |
| If we specify that <math>e \otimes f</math> is injective, i.e., its inverse is a function, then <math>(e \otimes f)^{-1}</math>
| |
| becomes a constructor function for records of type <math>R</math>.
| |
| | |
| This means that an open record structure can be 'closed-off' by the addition of an axiom stating that
| |
| the direct product of the fields is injective:
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{AXIOMS}~~~~~~\textit{ (Closing) }\\
| |
| ~~~~\begin{array}{l}
| |
| e \otimes f ~\in~ R \tinj (E\times F)
| |
| \end{array}
| |
| \end{array}
| |
| </math> | |
| |}
| |
| </center> | |
| | |
| Once this ''closing'' axiom is introduced, we can no longer introduce new fields to the record structure - at least
| |
| not without introducing an inconsistency. If we were to now add a field ''g'', the closing axiom would mean
| |
| that records whose ''e'' and ''f'' fields are the same, must be correspond to the same record ''r'' even if they differ
| |
| in the ''g'' field. But since ''g'' is a function, different ''g'' values cannot be related to the same record ''r''.
| |
| | |
| Regardless of whether the closing axiom is introduced, some feasibility proof obligations arising from the use of the
| |
| projection approach will require the existence of a record corresponding to any tuple of field components. This can be
| |
| specified by the following ''feasibility'' axiom stating that the product of the projections is surjective:
| |
| <center> | |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{AXIOMS}~~~~~~\textit{ (Feasibility) }\\
| |
| ~~~~\begin{array}{l}
| |
| e \otimes f ~\in~ R \tsur (E\times F)
| |
| \end{array}
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center> | |
| | |
| ==Recursive Structured Types==
| |
| | |
| It is well known how to deal with recursive records using the constructor approach.
| |
| This is explored further in the context of Event-B and Rodin as part of the mathematical extension
| |
| work where proposals for inductive datatypes are made (see [[Mathematical_extensions]]).
| |
| Inductive datatypes are defined by constructor functions similar to constructor-based records.
| |
| For example, to define lists we would use two disjoint constructors, ''nil'' and ''cons''.
| |
| The ''cons'' constructor for lists typically comes with two projections, ''head'' and ''tail''.
| |
| The structural induction principle for inductive datatypes is well known.
| |
| | |
| With the projection approach we can define two subtypes, for empty and non-empty lists,
| |
| and extend the non-empty subtype with ''head'' and ''tail'' projections.
| |
| <center>
| |
| {{SimpleHeader}}
| |
| |<math> \begin{array}{l}
| |
| \textbf{SETS}~~ T,~ Node\\
| |
| \textbf{CONSTANTS}~~ Nil,~ Cons\\
| |
| \textbf{AXIOMS}\\
| |
| ~~~~\begin{array}{l}
| |
| partition(~ Node, ~Nil,~ Cons ~)
| |
| \end{array} \\~\\
| |
| \textbf{EXTEND~~ RECORD}~~ \textit{Cons}~~\textbf{WITH}\\
| |
| ~~~~~~~~~~~~ head\in T \\
| |
| ~~~~~~~~~~~~ tail\in LIST
| |
| \end{array}
| |
| </math>
| |
| |}
| |
| </center>
| |
|
| |
|
| The appropriate induction principle for the projection based approach needs to be explored further.
| | ==Current Limitations== |
| | * Records are not supported by the Camille text editor (see warning below) |
| | * <s>Records are not supported by the Pretty print facility</s> |
| | * <s>Records are not supported by the Synthesis view facility</s> |
| | * Records are not supported by the EventB2Latex plug-in |
| | * <s>Records are not supported by the Refactoring plug-in</s> |
| | * Records are partially supported by the Decomposition plug-in (Machines that use records can be decomposed, but the Context that contains the record cannot). |
| | * Records may have, at most, one supertype. |
| | * <s>Records may only have records as supertypes (not carrier sets)</s> |
| | * <s>There is no finalisation of a record - hence make functions are not supported</s> |
|
| |
|
| ==Structured Variables== | | ==Warning== |
|
| |
|
| To be done...
| | Records are not supported in the Camille text editor. Editing a context that contains records with the Camille editor may result in the Records being lost. |
|
| |
|
| [[Category:Work in progress]] [[Category:Design]] | | [[Category:Work in progress]] [[Category:Design]] |
This page is under development. It is intended to be a user oriented manual for using records in Event-B. This page should be read in conjunction with the Structured Types page which gives a more theoretical description of the origin of the Records extension.
Introduction
The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures.
The Records Extension introduces a new modelling construct to provide a notion of structured types in Event-B Contexts.
Currently, structured variables are not supported. Variables that are typed as an instance of a record type can be thought of as identifying a particular record value. Hence it is not possible to vary an individual field, the variable must be assigned a complete new record value instance. To vary an individual field this new record value instance can be selected to have the same field value for every other field.)
UI Extensions
The Event-B editor is extended to include two new top level clauses. These are Record Declarations and Record Extensions.
Records (or sub-records) are introduced in the Record Declarations clause. Records that are introduced here without a Supertypes clause are equivalent to carrier sets. Those that have a Supertypes clause are equivalent to constants that are a subset of the referenced (i.e. subtyped) record or carrier set.
Record Extensions may only add new fields to a record that has previously been declared in a Record Declaration. The extended record is referenced in an 'extends' clause.
Record Declaration clause also contains a toggle button to control the record's closure property. A closed record cannot be subtyped by other records or extended by record extensions.
The Event-B navigator is extended to show a new node Records. Under this node are listed the records and records extensions in the Context.
Record Extensions are displayed as the name of the extended record appended with a + sign. Each record or record extension can be expanded to show the owned fields. (Note that this list is not cumulative, only the new fields are shown).
(Currently in the Navigator, the Records node is shown as the first item in the Context whereas eleswhere it appears between carrier sets and constants. This is due to a limitation in the Rodin tool extension facilities).
The Outline panel shows the records followed by record extensions as a plain list without the Records node. Again, the record or record extension can be expanded to show the fields.
In all cases, the icon used for a record reflects its equivalence. That is, if it does not have a supertypes clause, it is displayed with the same icon as a carrier set. otherwise it is displayed with the same icon as a constant.
Semantics of Records
The semantics of Records are given by their translation into 'pure' Event-B. This translation is performed by extensions to the static checker which generates a 'checked context' (.BCC file) containing pure Event-B from an unchecked (.BUC file) containing record elements. Hence the translated Event-B is not visible to the user.
[It may be instructive to open the *.bcc file with a text editor to examine the generated carrier sets, constants, and axioms]
Usage
First define Records in the Record Declarations section. Some of these can subtype others but you need at least one that is not a subset, i.e. has no supertypes. Note that we decided not to allow records to subtype or extend Carrier Sets, but you can do the equivalent by defining a record without any fields and subtyping/extending that. To be correctly static-checked record definitions must be in order of their referencing i.e. a subtype record would follow a supertype record which it references (to know about its type). In opposite case static checker will show a typing problem.
Add fields and give them a type by entering an expression that evaluates to a set. Note that this expression must be a basic type expression. You can use records, constants and sets in the expression.
After a record is defined it can be declared as closed using a toggle button in its Record Declaration clause. When record is closed it cannot be subtyped or extended anymore. Another effect of closing a record is that additional axioms are generated for it in the checked context. These include a closure axiom, a make-function for the record and an update-function for each of its fields (also for derived fields from supertype records). Another axiom — feasibility axiom — is generated for every record independent of its closure attribute.
For Record Extensions just select the record you want to add new fields to from the drop down list and then add the new fields. Only open (not closed) records can be extended, although the drop down list contains all the declared records.
You can refer to records and fields in axioms/theorems. E.g., you could define a constant to be an instance of a record. In all cases you can refer to records and fields in the current or visible abstract (extended*) contexts.
You use fields as if they were functions (which is what they are in the checked context).
e.g. if  belongs to
belongs to 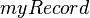 which has a field,
which has a field, 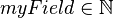 then I could write in a predicate
then I could write in a predicate 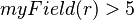 .
.
Proving With Records
The prover will refer to records as sets and constants, and to fields as constants. Therefore for proving you may need to be aware of this.
Axioms that are automatically generated for typing records and their fields will have automatically generated labels and these may be referenced in the prover interface.
The automatically generated labels use an easy to interpret format:
- Subtype Record typing axioms are in the format <recordName>.type<d> (where d is a decimal digit appended to ensure there are no name clashes)
- Field typing axioms are in the format <recordName>.<fieldName>.type<d> (where d is a decimal digit appended to ensure there are no name clashes)
Other axioms use record and field labels in their labelling, which leads to a longer and slightly confusing but still interpretable format:
- Feasibility axioms are in the format <recordName>.feasibility (or <recordName>.feasibility.ext<n> in case of record extensions)
- Closure axioms are in the format <recordName>.closure
- Make function's 1st axiom (function's typing) is in the format <recordName>.make.axm1
- Make function's 2nd axiom (for each field) is in the format <recordName>.<fieldName>.make.axm2
- Update function's 1st axiom (record field update function's typing) is in the format <recordName>.<fieldName>.update.axm1
- Update function's 2nd axiom (equivalence to record construction with a specific value of updated field) is in the format <recordName>.<fieldName>.update.axm2
Current Limitations
- Records are not supported by the Camille text editor (see warning below)
Records are not supported by the Pretty print facilityRecords are not supported by the Synthesis view facility- Records are not supported by the EventB2Latex plug-in
Records are not supported by the Refactoring plug-in- Records are partially supported by the Decomposition plug-in (Machines that use records can be decomposed, but the Context that contains the record cannot).
- Records may have, at most, one supertype.
Records may only have records as supertypes (not carrier sets)There is no finalisation of a record - hence make functions are not supported
Warning
Records are not supported in the Camille text editor. Editing a context that contains records with the Camille editor may result in the Records being lost.
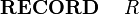
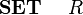
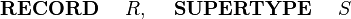
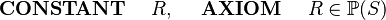
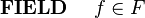
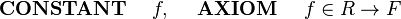
 belongs to
belongs to 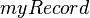 which has a field,
which has a field, 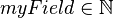 then I could write in a predicate
then I could write in a predicate 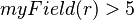 .
.