User:Nicolas/Collections/ADVANCE D3.4 Model Checking: Difference between revisions
imported>Ladenberger |
imported>Nicolas m →LTL Fairness: LTL^[e] -> LTL<sup>[e]</sup> |
||
| (24 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== Overview == | == Overview == | ||
In this period we have worked on scalability of the tools, by improving ProB for theories, for the WP1 and WP2 case study demands, and by adding dedicated support for fairness properties. | |||
We have also provided a link to the TLC model checker for large state space of more concrete formal models. | |||
We have also added new features to the model checking core of ProB, in feedback from the other work packages. | |||
== Motivations / Decisions == | == Motivations / Decisions == | ||
=== LTL | === Linear Temporal Logic === | ||
LTL is a specification language used for specifying temporal properties of a system. A possible requirement that could refer to WP1 may be, for example, ''once a block is reserved, it will eventually be occupied''. The requirement could be easily written as an LTL formula using the temporal operators `G` (always) and `F` (eventually): | |||
`G ({reserved(B) = TRUE} => F {occupied(B) = TRUE})`, where ''B'' is a block of some track segment in the railway network and the expressions inside the curly brackets `{...}` are B predicates. | |||
Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled actions imposed by the user as fair constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL<sup>e</sup> formula intended to be checked. For example, for a given LTL<sup>e</sup> formula "f" a set of weak fairness conditions {e1,…,en} (where e1,...,en are some events) can be given as follows: | ==== LTL Fairness ==== | ||
ProB provides support for checking temporal properties expressed by means of LTL (Linear Temporal Logic) or CTL (Computation Tree Logic).<ref name="LTLpaper">D. Plagge and M. Leuschel: ''Seven at one stroke: LTL model checking for High-level Specifications in B, Z, CSP, and more''. STTT, 12(1): 9-21, Feb 2010</ref> In ProB linear temporal properties can be expressed by an extended version of LTL, denoted as LTL<sup>[e]</sup>, which additionally enables the user to set propositions on transitions. Writing propositions on transitions is allowed by using the constructs `e(...)` and `[...]`. (For more information on the syntax and semantics of LTL<sup>[e]</sup> consult <ref name="LTL">ProB User Manual: LTL Model Checking, http://www.stups.uni-duesseldorf.de/ProB/index.php5/LTL_Model_Checking</ref>.) | |||
Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled actions imposed by the user as fair constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL<sup>[e]</sup> formula intended to be checked. For example, for a given LTL<sup>[e]</sup> formula "f" a set of weak fairness conditions {e1,…,en} (where e1,...,en are some events) can be given as follows: | |||
(FG e(e1) => GF [e1]) & … & (FG e(en) => GF [en]) => f. | (FG e(e1) => GF [e1]) & … & (FG e(en) => GF [en]) => f. | ||
In a similar way, strong fairness constraints can be imposed expressed by means of an | In a similar way, strong fairness constraints can be imposed expressed by means of an LTL<sup>[e]</sup> formula: | ||
(GF e(e1) => GF [e1]) & … & (GF e(en) => GF [en]) => f. | (GF e(e1) => GF [e1]) & … & (GF e(en) => GF [en]) => f. | ||
Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula <ref>O. Lichtenstein and A. Pnueli: ''Checking that Finite State Concurrent Programs Satisfy Their Linear Specification''. POPL '85, Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, ACM, 1985</ref> <ref> | Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula <ref>O. Lichtenstein and A. Pnueli: ''Checking that Finite State Concurrent Programs Satisfy Their Linear Specification''. POPL '85, Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, ACM, 1985</ref> <ref name="LTLpaper"> </ref>. | ||
For this reason, the search algorithm of the LTL model checker in ProB has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to | For this reason, the search algorithm of the LTL model checker in ProB has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to ProB’s LTL parser for setting fairness constraints to an LTL<sup>[e]</sup> property. The new operators are WF(-) and SF(-) and both accept as argument an operation. The fairness constraints must be given by means of implication: "fair => f", where "f" is the property to be checked and "fair" the fairness constraints. | ||
In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively. | In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively. | ||
| Line 27: | Line 38: | ||
** `&` and `or`: conjunction and disjunction | ** `&` and `or`: conjunction and disjunction | ||
More information on setting fairness to LTL formulas and the LTL Model Checker is available on the ProB User Manual website <ref> | More information on setting fairness to LTL formulas and the LTL Model Checker is available on the ProB User Manual website <ref name="LTL"> </ref>. | ||
==== Use Case ==== | ===== Use Case ===== | ||
Consider an Event-B model | Consider an Event-B model formalizing an algorithm for mutual exclusion with semaphores for two concurrent processes <math>P_1</math> and <math>P_2</math>. Each process has been simplified to perform three types of events: ''request'' (for entering in the critical section), ''enter'' (entering the critical section), and ''release'' (exiting the critical section). (For more information on the algorithm and the design of the model see <ref>C.Baier and J.-P. Katoen. “Principles of Model Checking”, The MIT Press, 2008, pages 43-45.</ref>). | ||
Each of the actions of a process are represented by | Each of the actions of a process are represented by a respective event: | ||
[[File:MUTEX_Events_horizontal.png]] | |||
Each process <math>P_i</math> has three possible states that are denoted by the constants <math>noncrit_{i}</math> (the state in which <math>P_i</math> performs noncritical actions), <math>wait_{i}</math> (the state in which <math>P_{i}</math> waits to enter the critical section), and <math>crit_{i}</math> (representing the state in which <math>P_{i}</math> is in the critical section). Both processes share the binary semaphore y where y=1 indicates that the semaphore is free and y=0 that the semaphore is currently processed by one of the processes. | Each process <math>P_i</math> has three possible states that are denoted by the constants <math>noncrit_{i}</math> (the state in which <math>P_i</math> performs noncritical actions), <math>wait_{i}</math> (the state in which <math>P_{i}</math> waits to enter the critical section), and <math>crit_{i}</math> (representing the state in which <math>P_{i}</math> is in the critical section). Both processes share the binary semaphore y where y=1 indicates that the semaphore is free and y=0 that the semaphore is currently processed by one of the processes. | ||
There are several requirements that the mutual exclusion algorithm should satisfy. The most important one is the mutual exclusion property that says always at most one process is in its critical section. This can be simply expressed, for example, as an invariant of the respective Event-B model: not(p1 = crit1 & p2 = crit2). However, there are other properties that can be easily expressed by means of LTL formulas and automatically checked on the model. For example, the requirement each process will enter infinitely often its critical section can be specified by the LTL formula `GF {p1 = crit1} & GF {p2 = crit2}` or the starvation freedom property that states each waiting process will eventually enter its critical section: | There are several requirements that the mutual exclusion algorithm should satisfy. The most important one is the mutual exclusion property that says ''always at most one process is in its critical section''. This can be simply expressed, for example, as an invariant of the respective Event-B model: not(p1 = crit1 & p2 = crit2). However, there are other properties that can be easily expressed by means of LTL formulas and automatically checked on the model. For example, the requirement ''each process will enter infinitely often its critical section'' can be specified by the LTL formula `GF {p1 = crit1} & GF {p2 = crit2}` or the starvation freedom property that states ''each waiting process will eventually enter its critical section'': | ||
G ({p1 = wait1} => F {p1 = crit1}) & G ({p2 = wait2} => F {p2=crit2}) | G ({p1 = wait1} => F {p1 = crit1}) & G ({p2 = wait2} => F {p2=crit2}) | ||
Running the LTL model checker of ProB will provide for the last two properties above a counterexample since the model permits that a process may perform infinitely often consecutively the events request, enter and release, and in this way to ignore the other process infinitely. An example trace that describes this behavior could be <math>\langle Req2,Req1,Enter1,Rel1,Req1,Enter1,\ldots\rangle</math>. | Running the LTL model checker of ProB will provide for the last two properties above a counterexample since the model permits that a process may perform infinitely often consecutively the events ''request'', ''enter'' and ''release'', and in this way to ignore the other process infinitely. An example trace that describes this behavior could be <math>\langle Req2,Req1,Enter1,Rel1,Req1,Enter1,\ldots\rangle</math>. | ||
On the other hand, such behaviors can be considered as unrealistic computations for the | On the other hand, such behaviors can be considered as unrealistic computations for the eventual implementation of the algorithm. Therefore fairness constraints can be set in order to discard such behaviors. For example, checking the property ''process <math>P_1</math> will enter its critical section infinitely often'' (as LTL property: `GF {p1 = crit1}`) can be checked by restricting that the event `Req1` will not be continuously ignored and that the event `Enter1` will not be ignored infinitely often. Both conditions on the property can be given by means of an LTL<sup>[e]</sup> formula on the right side of the implication as follows: | ||
(FG e(Req1) => GF [Req1]) & (GF e(Enter1) => GF [Enter1]) => GF {p1 = crit1} | (FG e(Req1) => GF [Req1]) & (GF e(Enter1) => GF [Enter1]) => GF {p1 = crit1} | ||
For checking the formula the LTL model checker generates 13312 atoms and 7515 transitions and needs overall 509 ms to prove the property. On the other hand, using the extension of the LTL model checker for checking fairness (by entering the formula `WF(Req1) & SF(Enter1) => GF {p1=crit1}`), the model checker generates 32 atoms and 39 transitions (the atoms and transitions generated just for `GF {p1 = crit1}`) and an overall time of 50 ms. | For checking the formula the LTL model checker generates 13312 atoms and 7515 transitions and needs overall 509 ms to prove the property. On the other hand, using the extension of the LTL model checker for checking fairness (by entering the formula `WF(Req1) & SF(Enter1) => GF {p1=crit1}`), the model checker generates 32 atoms and 39 transitions (the atoms and transitions generated just for `GF {p1 = crit1}`) and an overall time of 50 ms. | ||
For checking the requirement each process will enter infinitely often its critical section the LTL formula ` GF {p1 = crit1} & GF {p2 = crit2}` should be checked with the following fairness constraints: | For checking the requirement ''each process will enter infinitely often its critical section'' the LTL formula ` GF {p1 = crit1} & GF {p2 = crit2}` should be checked with the following fairness constraints: | ||
(WF(Req1) & WF(Req2)) & (SF(Enter1) & SF(Enter2)) | (WF(Req1) & WF(Req2)) & (SF(Enter1) & SF(Enter2)) | ||
Encoding these fairness conditions as an LTL<sup>e</sup> formula will blow up exponentially the number of atoms and the transitions and thus make practically impossible to check the above property in a reasonable time. | Encoding these fairness conditions as an LTL<sup>[e]</sup> formula will blow up exponentially the number of atoms and the transitions and thus make practically impossible to check the above property in a reasonable time. | ||
==== New LTL Patterns ==== | ==== New LTL Patterns ==== | ||
The ABZ landing gear case study <ref>F. Boniol, V. Wiels, “The Landing Gear System Case Study”, ABZ 2014</ref> was | The ABZ landing gear case study <ref>F. Boniol, V. Wiels, “The Landing Gear System Case Study”, ABZ 2014</ref> was formalized in Event-B and validated with ProB. <ref name="Landing Gear">D. Hansen, L. Ladenberger, H. Wiegard, J. Bendisposto, M. Leuschel, “Validation of the ABZ Landing Gear System using ProB”, ABZ 2014: The Landing Gear Case Study, 2014, pages 66-79, Springer International Publisher.</ref> In the course of the validation of the model new features have been developed in ProB for checking relative deadlock freedom and determinism. | ||
Since it has turned out that the features were a key part of the validation of the model and the authors believe that they will be of use for other Event-B system developments, the LTL model checker has been extended to support these features as new patterns within LTL<sup>e</sup> formulas: | Since it has turned out that the features were a key part of the validation of the model and the authors believe that they will be of use for other Event-B system developments, the LTL model checker has been extended to support these features as new patterns within LTL<sup>[e]</sup> formulas: | ||
* deadlock(e1,e2,...,ek), where e1,e2,...,ek with k>0 are events. Used to check relative deadlocks, more precisely to check if a set of events are disabled in a state. | * deadlock(e1,e2,...,ek), where e1,e2,...,ek with k>0 are events. Used to check relative deadlocks, more precisely to check if a set of events are disabled in a state. | ||
* deterministic(e1,e2,…,ek), where e1,e2,...,ek with k>0 are events. Used to check that maximum one of the events in the parentheses is enabled in a state. Note that if the atomic proposition is checked in a state where no one of the events e1,e2,...,ek is enabled, the test will succeed. | * deterministic(e1,e2,…,ek), where e1,e2,...,ek with k>0 are events. Used to check that maximum one of the events in the parentheses is enabled in a state. Note that if the atomic proposition is checked in a state where no one of the events e1,e2,...,ek is enabled, the test will succeed. | ||
* controller(e1,e2,…,ek) , where e1,e2,...,ek with k>0 are events. Used to check that exactly one of the events e1,e2,...,ek is enabled in a state. | * controller(e1,e2,…,ek), where e1,e2,...,ek with k>0 are events. Used to check that exactly one of the events e1,e2,...,ek is enabled in a state. | ||
Referring to the landing gear case study from <ref name="Landing Gear"> </ref>, one important issue in the process of validation of the model was to guarantee that the controller behaves in a determinisitc way. In the corresponding model the behavior of the controller is divided into several events: con_stop_stimulate_extend_gear_valve, con_stimulate_extend_gear_valve, con_stop_stimulate_retract_gear_valve, etc. The deterministic behavior of the controller could, for example, be tested by using new LTL pattern `deterministic(e1,e2,…,ek)` within an LTL<sup>[e]</sup> formula: | |||
G deterministic(con_stop_stimulate_extend_gear_valve,con_stimulate_extend_gear_valve,con_stop_stimulate_retract_gear_valve,...) | |||
and then check the LTL<sup>[e]</sup> formula with the ProB's LTL model checker. | |||
=== Theory Support === | === Theory Support === | ||
Theory Support was relevant for a variety of case studies, and is relevant for simulation, model checking and proving. | Theory Support was relevant for a variety of case studies, and is relevant for simulation, model checking and proving. | ||
We ensured that the Disprover also works with theories | We ensured that the Disprover also works with theories. | ||
We have also improved the constraint propagation of the ProB kernel for records and freetypes, which are used to represent Event-B inductive datatypes. | We have also improved the constraint propagation of the ProB kernel for records and freetypes, which are used to represent Event-B inductive datatypes. | ||
(As a side note, this feature is also being used | (As a side note, this feature is also being used for validating VDM specifications using ProB within the [http://overturetool.org Ouverture] tool <ref>Lausdahl, Kenneth; Ishikawa, Hiroshi; Larsen, Peter Gorm. Interpreting Implicit VDM Specifications using ProB. 2014. Abstract from 12th Overture Workshop on VDM, Newcastle, United Kingdom. http://wiki.overturetool.org/index.php/12th_Overture_Workshop.</ref>. Ouverture is the subject of ongoing and past EU projects, e.g., [http://destecs.org Destecs] or [http://www.compass-research.eu Compass].). | ||
Finally, the treatment of recursive functions within the ProB kernel has been improved, also in light of dealing with recursive operators of Event-B Theories. | Finally, the treatment of recursive functions within the ProB kernel has been improved, also in light of dealing with recursive operators of Event-B Theories. | ||
More details can be found in deliverable D4.4 (ProB constraint solving kernel). | |||
=== Physical Units === | === Physical Units === | ||
| Line 80: | Line 99: | ||
* Support for the analysis of units throughout refinement relations. | * Support for the analysis of units throughout refinement relations. | ||
* Support for abstract units like "length" that can later be concretised to standard SI units. | * Support for abstract units like "length" that can later be concretised to standard SI units. | ||
A journal version of the SEFM'13 article <ref>Sebastian Krings, Michael Leuschel, "Inferring Physical Units in B Models. SEFM'2013, LNCS 8137, p. 137-151."</ref> has been submitted. | |||
=== B to TLA+ === | === B to TLA+ === | ||
We are interested in validating the correctness of our translation from B to TLA+. | We developed a translation from B to TLA+ to verify B specifications with TLC. TLC is an explicit state model checker for TLA+ providing a parallel and a distributed mode. It is particularly good for lower level specifications, where it can be substantially faster than ProB's own model checker. | ||
Hence, we have conducted extensive tests to validate our approach. | |||
For example, we use a range of models encoding mathematical laws to stress test our translation. | Moreover, we are interested in validating the correctness of our translation from B to TLA+. Hence, we have conducted extensive tests to validate our approach. For example, we use a range of models encoding mathematical laws to stress test our translation. These have proven to be very useful for detecting bugs in our translation and libraries. In addition, we have uncovered a bug in the model checker TLC. Moreover, we use a wide variety of benchmarks, checking that ProB and TLC produce the same result and generate the same number of states | ||
These have proven to be very useful for detecting bugs in our translation and libraries. | |||
In addition, we have uncovered a bug in the model checker TLC. | |||
Moreover, we use a wide variety of benchmarks, checking that ProB and TLC produce the same result and generate the same number of states | |||
The current version of our translator covers almost all operators of a abstract B machine. | The current version of our translator covers almost all operators of a abstract B machine. | ||
Moreover, TLC can be used to validate liveness properties (LTL formulas) for B specifications under fairness conditions. | Moreover, TLC can be used to validate liveness properties (LTL formulas) for B specifications under fairness conditions. | ||
Our approach has been published at the ABZ’2014 conference in Toulouse. | Our approach has been published at the ABZ’2014 conference in Toulouse <ref>D. Hansen and M. Leuschel: ''Translating B to TLA + for Validation with TLC''. ABZ'14, LNCS 8477, p.40-55, June 2014</ref>. | ||
A technical report is available <ref>http://stups.hhu.de/w/Special:Publication/HansenLeuschel_TLC4B_techreport</ref>. | A technical report is available <ref>http://stups.hhu.de/w/Special:Publication/HansenLeuschel_TLC4B_techreport</ref>. | ||
=== Performance Improvements === | === Performance Improvements === | ||
Various performance improvements have been made to the model checker and animator for Event-B models, both in terms of memory consumption and speed. | Various performance improvements have been made to the model checker and animator for Event-B models, both in terms of memory consumption and speed. | ||
For example, the Event-B model of the Early parser by JR Abrial is now running an order of magnitude faster than before the beginning of the project. | For example, ProB now executes the models from WP1 and WP2 considerably faster than at the beginning of the project and than at the beginning of the last period of the project. | ||
Another example is an Event-B model of the Early parser by JR Abrial (a standard benchmark used for ProB regression testing) is now running an order of magnitude faster than before the beginning of the project. | |||
== Available Documentation == | == Available Documentation == | ||
'''ProB'''<br> | '''ProB'''<br> | ||
The ProB Website<ref>http://www.stups.uni-duesseldorf.de/ProB</ref> is the place where we collect information on the ProB toolset. There are several tutorials on ProB available in the User manual section. We also supply documentation on extending ProB for developers. | The ProB Website<ref>ProB Website: http://www.stups.uni-duesseldorf.de/ProB/</ref> is the place where we collect information on the ProB toolset. There are several tutorials on ProB available in the User manual section<ref>ProB User Manual: http://www.stups.uni-duesseldorf.de/ProB/index.php5/User_Manual</ref>. We also supply documentation on extending ProB for developers<ref>ProB Developer Manual: http://www.stups.uni-duesseldorf.de/ProB/index.php5/Developer_Manual</ref>. Documentation and tutorials on the new LTL features available<ref name="LTL"/>. Recently, a tutorial for the LTL counter-example view in Rodin has been written<ref>LTL View in Rodin: http://www.stups.uni-duesseldorf.de/ProB/index.php5/Tutorial_LTL_Counter-example_View</ref>. | ||
The physical unit support is explained here<ref>Unit Plugin: http://www.stups.uni-duesseldorf.de/ProB/index.php5/Tutorial_Unit_Plugin</ref>. | |||
The TLC for B model checking support is explained here<ref>TLC: http://www.stups.uni-duesseldorf.de/ProB/index.php5/TLC</ref>. | |||
In addition we run a bug tracking system<ref>Bug Tracking System: http://jira.cobra.cs.uni-duesseldorf.de/</ref> to document known bugs, workarounds and feature requests. | |||
== Conclusion == | == Conclusion == | ||
With TLC4B we have provided a new scalable model checking approach for low-level B models. It should be particularly interesting for hardware models or lower-level models with very large state spaces. | |||
Fairness is often important for real-life temporal properties; by adding these we have made the ProB LTL model checker much more convenient and effective to use. | |||
The new LTL patterns arose multiple times in the various case studies; by providing them directly within the LTL language we have made the specification task much easier. | |||
Finally, theories in Rodin are very important and have played an important role in both WP1 and WP2 case studies. | |||
The support provided by ProB was thus essential for the success in these work packages. | |||
== References == | == References == | ||
<references/> | <references/> | ||
Latest revision as of 10:31, 25 November 2014
Overview
In this period we have worked on scalability of the tools, by improving ProB for theories, for the WP1 and WP2 case study demands, and by adding dedicated support for fairness properties. We have also provided a link to the TLC model checker for large state space of more concrete formal models. We have also added new features to the model checking core of ProB, in feedback from the other work packages.
Motivations / Decisions
Linear Temporal Logic
LTL is a specification language used for specifying temporal properties of a system. A possible requirement that could refer to WP1 may be, for example, once a block is reserved, it will eventually be occupied. The requirement could be easily written as an LTL formula using the temporal operators `G` (always) and `F` (eventually):
`G ({reserved(B) = TRUE} => F {occupied(B) = TRUE})`, where B is a block of some track segment in the railway network and the expressions inside the curly brackets `{...}` are B predicates.
LTL Fairness
ProB provides support for checking temporal properties expressed by means of LTL (Linear Temporal Logic) or CTL (Computation Tree Logic).[1] In ProB linear temporal properties can be expressed by an extended version of LTL, denoted as LTL[e], which additionally enables the user to set propositions on transitions. Writing propositions on transitions is allowed by using the constructs `e(...)` and `[...]`. (For more information on the syntax and semantics of LTL[e] consult [2].)
Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled actions imposed by the user as fair constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL[e] formula intended to be checked. For example, for a given LTL[e] formula "f" a set of weak fairness conditions {e1,…,en} (where e1,...,en are some events) can be given as follows:
(FG e(e1) => GF [e1]) & … & (FG e(en) => GF [en]) => f.
In a similar way, strong fairness constraints can be imposed expressed by means of an LTL[e] formula:
(GF e(e1) => GF [e1]) & … & (GF e(en) => GF [en]) => f.
Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula [3] [1].
For this reason, the search algorithm of the LTL model checker in ProB has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to ProB’s LTL parser for setting fairness constraints to an LTL[e] property. The new operators are WF(-) and SF(-) and both accept as argument an operation. The fairness constraints must be given by means of implication: "fair => f", where "f" is the property to be checked and "fair" the fairness constraints.
In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively.
Basically, "wfair" and "sfair" are expressed by means of logical formulas having the following syntax:
- Weak fair conditions ("wfair"):
- `WF(a)`, where `a` is an operation
- `&` and `or`: conjunction and disjunction
- Strong fair conditions ("sfair"):
- `SF(a)`, where `a` is an operation
- `&` and `or`: conjunction and disjunction
More information on setting fairness to LTL formulas and the LTL Model Checker is available on the ProB User Manual website [2].
Use Case
Consider an Event-B model formalizing an algorithm for mutual exclusion with semaphores for two concurrent processes 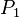 and
and 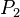 . Each process has been simplified to perform three types of events: request (for entering in the critical section), enter (entering the critical section), and release (exiting the critical section). (For more information on the algorithm and the design of the model see [4]).
. Each process has been simplified to perform three types of events: request (for entering in the critical section), enter (entering the critical section), and release (exiting the critical section). (For more information on the algorithm and the design of the model see [4]).
Each of the actions of a process are represented by a respective event:
Each process 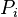 has three possible states that are denoted by the constants
has three possible states that are denoted by the constants 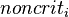 (the state in which
(the state in which 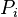 performs noncritical actions),
performs noncritical actions), 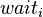 (the state in which
(the state in which 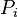 waits to enter the critical section), and
waits to enter the critical section), and 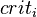 (representing the state in which
(representing the state in which 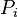 is in the critical section). Both processes share the binary semaphore y where y=1 indicates that the semaphore is free and y=0 that the semaphore is currently processed by one of the processes.
is in the critical section). Both processes share the binary semaphore y where y=1 indicates that the semaphore is free and y=0 that the semaphore is currently processed by one of the processes.
There are several requirements that the mutual exclusion algorithm should satisfy. The most important one is the mutual exclusion property that says always at most one process is in its critical section. This can be simply expressed, for example, as an invariant of the respective Event-B model: not(p1 = crit1 & p2 = crit2). However, there are other properties that can be easily expressed by means of LTL formulas and automatically checked on the model. For example, the requirement each process will enter infinitely often its critical section can be specified by the LTL formula `GF {p1 = crit1} & GF {p2 = crit2}` or the starvation freedom property that states each waiting process will eventually enter its critical section:
G ({p1 = wait1} => F {p1 = crit1}) & G ({p2 = wait2} => F {p2=crit2})
Running the LTL model checker of ProB will provide for the last two properties above a counterexample since the model permits that a process may perform infinitely often consecutively the events request, enter and release, and in this way to ignore the other process infinitely. An example trace that describes this behavior could be 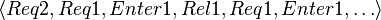 .
.
On the other hand, such behaviors can be considered as unrealistic computations for the eventual implementation of the algorithm. Therefore fairness constraints can be set in order to discard such behaviors. For example, checking the property process 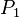 will enter its critical section infinitely often (as LTL property: `GF {p1 = crit1}`) can be checked by restricting that the event `Req1` will not be continuously ignored and that the event `Enter1` will not be ignored infinitely often. Both conditions on the property can be given by means of an LTL[e] formula on the right side of the implication as follows:
will enter its critical section infinitely often (as LTL property: `GF {p1 = crit1}`) can be checked by restricting that the event `Req1` will not be continuously ignored and that the event `Enter1` will not be ignored infinitely often. Both conditions on the property can be given by means of an LTL[e] formula on the right side of the implication as follows:
(FG e(Req1) => GF [Req1]) & (GF e(Enter1) => GF [Enter1]) => GF {p1 = crit1}
For checking the formula the LTL model checker generates 13312 atoms and 7515 transitions and needs overall 509 ms to prove the property. On the other hand, using the extension of the LTL model checker for checking fairness (by entering the formula `WF(Req1) & SF(Enter1) => GF {p1=crit1}`), the model checker generates 32 atoms and 39 transitions (the atoms and transitions generated just for `GF {p1 = crit1}`) and an overall time of 50 ms.
For checking the requirement each process will enter infinitely often its critical section the LTL formula ` GF {p1 = crit1} & GF {p2 = crit2}` should be checked with the following fairness constraints:
(WF(Req1) & WF(Req2)) & (SF(Enter1) & SF(Enter2))
Encoding these fairness conditions as an LTL[e] formula will blow up exponentially the number of atoms and the transitions and thus make practically impossible to check the above property in a reasonable time.
New LTL Patterns
The ABZ landing gear case study [5] was formalized in Event-B and validated with ProB. [6] In the course of the validation of the model new features have been developed in ProB for checking relative deadlock freedom and determinism.
Since it has turned out that the features were a key part of the validation of the model and the authors believe that they will be of use for other Event-B system developments, the LTL model checker has been extended to support these features as new patterns within LTL[e] formulas:
- deadlock(e1,e2,...,ek), where e1,e2,...,ek with k>0 are events. Used to check relative deadlocks, more precisely to check if a set of events are disabled in a state.
- deterministic(e1,e2,…,ek), where e1,e2,...,ek with k>0 are events. Used to check that maximum one of the events in the parentheses is enabled in a state. Note that if the atomic proposition is checked in a state where no one of the events e1,e2,...,ek is enabled, the test will succeed.
- controller(e1,e2,…,ek), where e1,e2,...,ek with k>0 are events. Used to check that exactly one of the events e1,e2,...,ek is enabled in a state.
Referring to the landing gear case study from [6], one important issue in the process of validation of the model was to guarantee that the controller behaves in a determinisitc way. In the corresponding model the behavior of the controller is divided into several events: con_stop_stimulate_extend_gear_valve, con_stimulate_extend_gear_valve, con_stop_stimulate_retract_gear_valve, etc. The deterministic behavior of the controller could, for example, be tested by using new LTL pattern `deterministic(e1,e2,…,ek)` within an LTL[e] formula:
G deterministic(con_stop_stimulate_extend_gear_valve,con_stimulate_extend_gear_valve,con_stop_stimulate_retract_gear_valve,...)
and then check the LTL[e] formula with the ProB's LTL model checker.
Theory Support
Theory Support was relevant for a variety of case studies, and is relevant for simulation, model checking and proving. We ensured that the Disprover also works with theories. We have also improved the constraint propagation of the ProB kernel for records and freetypes, which are used to represent Event-B inductive datatypes. (As a side note, this feature is also being used for validating VDM specifications using ProB within the Ouverture tool [7]. Ouverture is the subject of ongoing and past EU projects, e.g., Destecs or Compass.). Finally, the treatment of recursive functions within the ProB kernel has been improved, also in light of dealing with recursive operators of Event-B Theories. More details can be found in deliverable D4.4 (ProB constraint solving kernel).
Physical Units
The physical units analysis has been further stabilised, several reported bugs have been fixed. Support for physical units has been extended to theories along with the general theory-related improvements of ProB mentioned in the previous paragraph. The plug-in was ported to Rodin 3, all bugfixes and changes could be back ported to Rodin 2 successfully.
Further extension to the unit analysis include:
- Support for the analysis of units throughout refinement relations.
- Support for abstract units like "length" that can later be concretised to standard SI units.
A journal version of the SEFM'13 article [8] has been submitted.
B to TLA+
We developed a translation from B to TLA+ to verify B specifications with TLC. TLC is an explicit state model checker for TLA+ providing a parallel and a distributed mode. It is particularly good for lower level specifications, where it can be substantially faster than ProB's own model checker.
Moreover, we are interested in validating the correctness of our translation from B to TLA+. Hence, we have conducted extensive tests to validate our approach. For example, we use a range of models encoding mathematical laws to stress test our translation. These have proven to be very useful for detecting bugs in our translation and libraries. In addition, we have uncovered a bug in the model checker TLC. Moreover, we use a wide variety of benchmarks, checking that ProB and TLC produce the same result and generate the same number of states
The current version of our translator covers almost all operators of a abstract B machine. Moreover, TLC can be used to validate liveness properties (LTL formulas) for B specifications under fairness conditions. Our approach has been published at the ABZ’2014 conference in Toulouse [9]. A technical report is available [10].
Performance Improvements
Various performance improvements have been made to the model checker and animator for Event-B models, both in terms of memory consumption and speed. For example, ProB now executes the models from WP1 and WP2 considerably faster than at the beginning of the project and than at the beginning of the last period of the project. Another example is an Event-B model of the Early parser by JR Abrial (a standard benchmark used for ProB regression testing) is now running an order of magnitude faster than before the beginning of the project.
Available Documentation
ProB
The ProB Website[11] is the place where we collect information on the ProB toolset. There are several tutorials on ProB available in the User manual section[12]. We also supply documentation on extending ProB for developers[13]. Documentation and tutorials on the new LTL features available[2]. Recently, a tutorial for the LTL counter-example view in Rodin has been written[14].
The physical unit support is explained here[15].
The TLC for B model checking support is explained here[16].
In addition we run a bug tracking system[17] to document known bugs, workarounds and feature requests.
Conclusion
With TLC4B we have provided a new scalable model checking approach for low-level B models. It should be particularly interesting for hardware models or lower-level models with very large state spaces. Fairness is often important for real-life temporal properties; by adding these we have made the ProB LTL model checker much more convenient and effective to use. The new LTL patterns arose multiple times in the various case studies; by providing them directly within the LTL language we have made the specification task much easier. Finally, theories in Rodin are very important and have played an important role in both WP1 and WP2 case studies. The support provided by ProB was thus essential for the success in these work packages.
References
- ↑ 1.0 1.1 D. Plagge and M. Leuschel: Seven at one stroke: LTL model checking for High-level Specifications in B, Z, CSP, and more. STTT, 12(1): 9-21, Feb 2010
- ↑ 2.0 2.1 2.2 ProB User Manual: LTL Model Checking, http://www.stups.uni-duesseldorf.de/ProB/index.php5/LTL_Model_Checking
- ↑ O. Lichtenstein and A. Pnueli: Checking that Finite State Concurrent Programs Satisfy Their Linear Specification. POPL '85, Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, ACM, 1985
- ↑ C.Baier and J.-P. Katoen. “Principles of Model Checking”, The MIT Press, 2008, pages 43-45.
- ↑ F. Boniol, V. Wiels, “The Landing Gear System Case Study”, ABZ 2014
- ↑ 6.0 6.1 D. Hansen, L. Ladenberger, H. Wiegard, J. Bendisposto, M. Leuschel, “Validation of the ABZ Landing Gear System using ProB”, ABZ 2014: The Landing Gear Case Study, 2014, pages 66-79, Springer International Publisher.
- ↑ Lausdahl, Kenneth; Ishikawa, Hiroshi; Larsen, Peter Gorm. Interpreting Implicit VDM Specifications using ProB. 2014. Abstract from 12th Overture Workshop on VDM, Newcastle, United Kingdom. http://wiki.overturetool.org/index.php/12th_Overture_Workshop.
- ↑ Sebastian Krings, Michael Leuschel, "Inferring Physical Units in B Models. SEFM'2013, LNCS 8137, p. 137-151."
- ↑ D. Hansen and M. Leuschel: Translating B to TLA + for Validation with TLC. ABZ'14, LNCS 8477, p.40-55, June 2014
- ↑ http://stups.hhu.de/w/Special:Publication/HansenLeuschel_TLC4B_techreport
- ↑ ProB Website: http://www.stups.uni-duesseldorf.de/ProB/
- ↑ ProB User Manual: http://www.stups.uni-duesseldorf.de/ProB/index.php5/User_Manual
- ↑ ProB Developer Manual: http://www.stups.uni-duesseldorf.de/ProB/index.php5/Developer_Manual
- ↑ LTL View in Rodin: http://www.stups.uni-duesseldorf.de/ProB/index.php5/Tutorial_LTL_Counter-example_View
- ↑ Unit Plugin: http://www.stups.uni-duesseldorf.de/ProB/index.php5/Tutorial_Unit_Plugin
- ↑ TLC: http://www.stups.uni-duesseldorf.de/ProB/index.php5/TLC
- ↑ Bug Tracking System: http://jira.cobra.cs.uni-duesseldorf.de/
