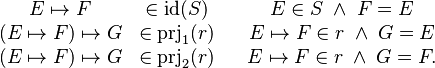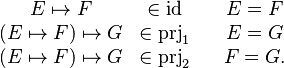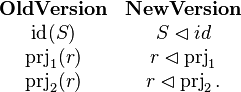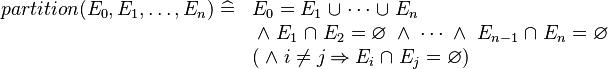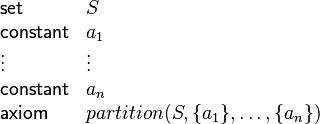Changes to the Mathematical Language of Event-B: Difference between revisions
imported>Nicolas |
imported>Nicolas |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
This document describes the evolution of the Event-B mathematical language that | This document describes the evolution of the Event-B mathematical language that happened in release 1.0.0. See [[Event-B_Mathematical_Language]] for a full description of the language. | ||
== Identity and Projections == | == Generic Identity and Projections == | ||
Three operators were still unary while they could be atomic: | Three operators were still unary while they could be atomic and generic: | ||
* the identity relation <math>\id</math> | * the identity relation <math>\id</math> | ||
* the first projection <math>\prjone</math> | * the first projection <math>\prjone</math> | ||
* the second projection <math>\prjtwo</math> | * the second projection <math>\prjtwo</math> | ||
These operators are defined as follows: | These operators are defined as follows in the old version: | ||
<math> | <math> | ||
\begin{matrix} | \begin{matrix} | ||
E\mapsto F &\in\id(S) && E\in S\;\land\; F = E\\ | E\mapsto F &\in\id(S) && E\in S\;\land\; F = E\\ | ||
(E\mapsto F)\mapsto G &\in\prjone(r) | (E\mapsto F)\mapsto G &\in\prjone(r) | ||
| Line 17: | Line 17: | ||
(E\mapsto F)\mapsto G &\in\prjtwo(r) | (E\mapsto F)\mapsto G &\in\prjtwo(r) | ||
&& E\mapsto F\in r\;\land\; G = F . | && E\mapsto F\in r\;\land\; G = F . | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
If we drop the parameter, we get | If we drop the parameter, we get | ||
| Line 24: | Line 24: | ||
operator. The new definitions are | operator. The new definitions are | ||
<math> | <math> | ||
\begin{matrix} | \begin{matrix} | ||
E\mapsto F &\in\id && E = F\\ | E\mapsto F &\in\id && E = F\\ | ||
(E\mapsto F)\mapsto G &\in\prjone && E = G\\ | (E\mapsto F)\mapsto G &\in\prjone && E = G\\ | ||
(E\mapsto F)\mapsto G &\in\prjtwo && F = G . | (E\mapsto F)\mapsto G &\in\prjtwo && F = G . | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
We have the following equivalence between the old | We have the following equivalence between the old | ||
and the new versions of the operators | and the new versions of the operators | ||
<math> | <math> | ||
\begin{matrix} | \begin{matrix} | ||
\textbf{Old Version} & \textbf{New Version}\\ | \textbf{Old Version} & \textbf{New Version}\\ | ||
\id(S) & S\domres id\\ | \id(S) & S\domres id\\ | ||
\prjone(r) & r\domres\prjone\\ | \prjone(r) & r\domres\prjone\\ | ||
\prjtwo(r) & r\domres\prjtwo . | \prjtwo(r) & r\domres\prjtwo . | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
Moreover, in the case where the parameter is not needed, then it can | Moreover, in the case where the parameter is not needed, then it can | ||
| Line 48: | Line 48: | ||
to express that a relation <math>r</math> is irreflexive, one would now write | to express that a relation <math>r</math> is irreflexive, one would now write | ||
<math>r\binter\id = \emptyset</math>. | <math>r\binter\id = \emptyset</math>. | ||
== Partition == | == Partition == | ||
| Line 56: | Line 54: | ||
<math> | <math> | ||
\begin{ | \begin{array}{ll} | ||
partition(E_0, E_1, \ldots, E_n)\defi & | partition(E_0, E_1, \ldots, E_n)\defi & | ||
E_0 = E_1\bunion \cdots\bunion E_n \\ & | E_0 = E_1\bunion \cdots\bunion E_n \\ & | ||
| Line 63: | Line 61: | ||
\;\land\; E_{n-1}\binter E_n = \emptyset \\ & | \;\land\; E_{n-1}\binter E_n = \emptyset \\ & | ||
(\;\land\; i \ne j \limp E_i \binter E_j = \emptyset ) \\ | (\;\land\; i \ne j \limp E_i \binter E_j = \emptyset ) \\ | ||
\end{ | \end{array} | ||
</math> | </math> | ||
| Line 80: | Line 78: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
which is a particular case of a set being defined by listing all its elements. | |||
=== Partition Wizard === | |||
{{TODO}} | |||
== Operator Associativity == | == Operator Associativity == | ||
Operators used to build sets of relations or functions, viz. | |||
* relation | |||
* total relation | |||
* surjective relation | |||
* total surjective relation | |||
* partial function | |||
* total function | |||
* partial injection | |||
* total injection | |||
* partial surjection | |||
* total surjection | |||
* bijection | |||
have no more relative priorities and loose associativity. Instead, users have to make it explicit by entering parenthesis in formulas. | |||
[[Category:Event-B]] | |||
[[Category:User documentation]] | |||
Latest revision as of 12:38, 17 April 2009
This document describes the evolution of the Event-B mathematical language that happened in release 1.0.0. See Event-B_Mathematical_Language for a full description of the language.
Generic Identity and Projections
Three operators were still unary while they could be atomic and generic:
- the identity relation
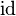
- the first projection
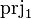
- the second projection
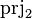
These operators are defined as follows in the old version:
If we drop the parameter, we get much more straightforward definitions that capture the essence of the operator. The new definitions are
We have the following equivalence between the old and the new versions of the operators
Moreover, in the case where the parameter is not needed, then it can
be dropped altogether: no domain restriction is needed. For instance,
to express that a relation  is irreflexive, one would now write
is irreflexive, one would now write
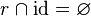 .
.
Partition
A new partition predicate is introduced. It is intended to provide an easier way to enter enumerated sets, while getting rid of the 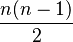 axioms needed to express pairwise distinctness (or disjointness). The partition operator is defined as follows:
axioms needed to express pairwise distinctness (or disjointness). The partition operator is defined as follows:
where the 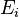 are expressions bearing the same type.
are expressions bearing the same type.
Then, we can enter into a context :
which is a particular case of a set being defined by listing all its elements.
Partition Wizard
TODO
Operator Associativity
Operators used to build sets of relations or functions, viz.
- relation
- total relation
- surjective relation
- total surjective relation
- partial function
- total function
- partial injection
- total injection
- partial surjection
- total surjection
- bijection
have no more relative priorities and loose associativity. Instead, users have to make it explicit by entering parenthesis in formulas.