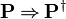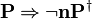Variations in HYP, CNTR and GenMP

This page describes the introduction of variations in the HYP, HYP_OR, CNTR and GENMP reasoners.

Context

The reasoners implementing the inference rules

HYP

,

HYP_OR

,

CNTR

and

GENMP_*

look for exact matches of a predicate. But, quite often, a similar predicate that does not match exactly (e.g., because it has been normalized) would suffice. There is also the possibility that a variation which is equivalent to the predicate would be present. For instance, "¬ a = b" is equivalent to "¬ b = a". Finally, the reasoners shall also consider variations which are a sufficient condition for the rule. For instance, if the goal is "a ≤ b", then a hypothesis "a < b" is a sufficient condition to discharge the goal with

HYP

.

Objective

The point of this enhancement is therefore to increase the proof power of the considered reasoners by having them consider variations of the sought predicate.

Conventions

The variations in the Inference Rules page have been generated such that the following facts hold:

• $\textbf{P} \limp \textbf{P}^{\dagger}$
• $\textbf{P} \limp \lnot \textbf{nP}^{\dagger}$

Moreover, we consider only variations that are in normal form (that is invariant under rewriting by the auto-rewriter of the sequent prover). This is why the table does not contain predicates such as 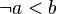$\lnot a < b$, but contain 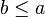$b\le a$ instead.

Implementation

This section explains how the variation have been implemented.

Variation Implementation

In order to simplify and optimize the generation of variation of the sought predicate, 4 functions (common to HYP, HYP_OR, CNTR and GenMP reasoners) have been implemented.

These functions have been defined as follows:

• StongerPositive(P) = $\{Q, Q \limp P\} \;\; (\lnot P \limp \lnot Q)$
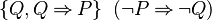
• WeakerPositive(P) = $\{Q, P \limp Q\} \;\; (\lnot Q \limp \lnot P )$
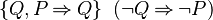
• StongerNegative(P) = $\{Q, Q \limp \lnot P\} \;\; (P \limp \lnot Q)$
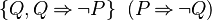
• WeakerNegative(P) = $\{Q, \lnot P \limp Q\} \;\; (\lnot Q \limp P )$

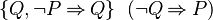
The above functions can be read as follows: The function returns the set of predicates Q from the predicate P by applying the corresponding rule. Each rule can be written in 2 implication, one for each sign of the predicate P.

Some optimisations, to reduce the number of implication to implement, have been implemented. Indeed, only the implications 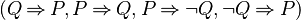$(Q \limp P, P \limp Q, P \limp \lnot Q, \lnot Q \limp P)$ have been implemented because they cover all cases. For instance, if the function StongerPositive takes a negative predicate as an input, the function returns a list of predicates stronger (e.g which infer) than the input. But it's also performed by the function StongerNegative. So this function applies the predicate negation and call to StongerNegative function.

Note: These functions assume the operators such as '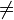$\neq$' have been removed by the normalization. Moreover, as explained in the convention part, the list of predicates returned contains only predicate in a normal form.

Reasoners Implementation

HYP, HYP_OR

The HYP reasoner generates a list of predicate wich are stronger than the goal (or disjunct). Thus, the sequent is discharged iff at least one hypothesis is contained into this list.

The HYP_OR reasoner proceed the same, for each disjunct a list of stronger predicate is generated if at least one hypothesis is contained into these lists the sequent is dicharged.

CNTR

Checks if the predicate to contradict is not null and it is contained into the hypotheses.

If the hypothesis to contradict is a positive predicate, it generates a list of predicates wich inferr the predicate. Else, it splits a conjunctive hypothesis if necessary into its conjuncts and compute for each conjuncts a list of predicate wich inferr the negation of the predicate (or conjunct). Finally, it saves into the list named neededHyps the hypotheses contained into the lists previously computed (hypotheses which contradict the given hypothesis).

GEN_MP

First, it extracts all predicates (unless predicates 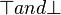$\btrue and \bfalse$) from the hypotheses. For each hypothesis its computes:

• a list of predicate which could be remplace by 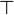$\btrue$ and which are weaker than the hypothesis.
• a list of predicate which could be remplace by 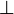$\bfalse$ and which are stronger than the negation of the hypothesis.

Then, it extracts the goal or the disjuncts if the sequent contain a goal in a disjunctive form. For each predicate its computes:

• a list of predicate which could be remplace by 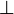$\bfalse$ and which are stronger than the hypothesis.
• a list of predicate which could be remplace by 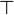$\btrue$ and which are weaker than the negation of the hypothesis.

For each substitution computed the following informations are stored:

• predicate original (hypothesis or goal)
• a boolean tells if the substitution comes from the goal
• the sub-predicate to substitute
• the substitue $( \btrue / \bfalse )$

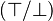
In order to simplify predicate search algorithm (avoid sign distinction), the sub-predicate should be postive.

Afterwards, each predicate extracted from hypotheses or the goal is traversed to get the list of possible applications of substitutes while ensuring that a given predicate could'nt be rewritten by himself. A possible applications of substitutes corresponds to a position into the predicate to rewrite and a sustitute.

Finally, the goal is re-written using the applications of substitutes computed and Then, the re-written goal and the hypotheses needed to achieve it are stored. Then the hypothese are re-written by producing new hypothesis actions.

Note: This improvement corresponds to the level 2 of GenMP.

Performances

Configuration

System:

• Intel(R) Core(TM) i7-4770 CPU @ (8* 3.40GHz)
• 24 Go RAM

OS:

• Ubuntu 12.04.3 LTS
• linux kernel 3.5.0-43

Java:

• java-7-openjdk-i386
• VM arguments
  • -Xms512m
  • -Xmx1024m

Eclipse:

• Indigo (3.7.2)

Benchmark Projects

The Rodin projects have been taken from the Deploy archives.

Protocol

A measurement is launched using the plug-in org.eventb.seqprover.core.perf.app. Tests are run from a launched eclipse application.

Launch Configuration must include exactly the following plug-ins:

• org.eventb.core
• org.eventb.core.seqprover
• org.eventb.core.ast
• org.rodinp.core
• org.eventb.core.seqprover.core.per.app

Add the following program argument:

• -application org.eventb.smt.core.perf.app.main <project-dir>

where <project-dir> is the path of the directory where is contained the Rodin projects.

Verify that 1024 Mo are free when tests are ready for launch.

First, it checks that the program argument is a directory and then it imports all Rodin projects from the directory into a workspace. The Auto-prover is applied on all Rodin Projects. For each Rodin project the following informations are displayed : "Project: Number of POs discharged/Number of POs". Finally, the proof files are strored into a directory named "Results" at the same level as the directory which contain the Rodin Project.

Tests

• Previous version : commit 69e0ae43a1
• New version : commit 2ea1cf6ffe

Results

The following results are means of measures on the Auto-prover

Measures

Projects	Number Of POs	Number Of POs discharged (previous version)	Number Of POs discharged (new version)
Doors	108	24	24
ssf	60	11	11
ch915_rev	31	9	9
Celebrity	46	11	11
search_backward	31	8	8
ch916_doors	103	26	26
B2B_mini_pilot_080806	498	272	280
DynamicStableLSR_090624	390	171	171
SimpleLyra	55	33	33
paper_pomc	85	29	30
ch7_conc	248	152	155
ch912_mobile	153	57	57
routing_new	241	86	86
ch915_inv	32	17	18
FloodSet	244	102	103
Rabin-110907	209	70	70
DSAOCSSv003	90	35	35
ch917_train	133	49	49
CDIS	91	40	40
Zer_ess	55	27	27
search_proved	31	10	10
mode_su_12	439	366	382
search	31	10	10
Club-120130	57	21	22
ch2_car	237	143	168
Cowboy-110905	16	9	9
ch915_mini	25	5	5
society_sol	9	0	0
gcd	175	105	105
pattern_poor	88	69	70
ch913_ieee	67	21	21
A2A_081216	276	161	168
ch910_ring	28	8	8
HermanRing-110906	58	24	24
ch911_tree	81	34	36
BoschSwitch	19	9	9
ch4_brp	127	83	86
ProofMethod-130117	14	4	4
ch915_bin	37	12	13
ParkingLot	10	4	4
Galois	1	0	0
ch915_search	17	10	10
ch915_sqrt	17	9	9
ch915_sort	67	25	25
society	7	0	0
BepiColombo_Models_v6.4	155	90	90
proof_obligations	39	18	18
DepSatSpec015Model000	1858	672	1300
ch6_brp	149	100	103
press	60	42	54
SSF_minipilot	24	6	6
ch4_file_1	52	21	21
SignalControl-110527	135	88	93
ResponseCoalitionNormative	178	40	40
ch8_circ_arbiter	153	114	128
pattern_rich	128	112	112
Modes_v2	121	50	50
DiningCryptSpec-100406	24	15	15
Mini_doors	12	4	4
ResponseCoalitionPerturbed	227	42	42
family_sol	9	1	1
Total	7683	3564	3914

Measures

Projects	Number Of POs	Time (previous version)	Time (new version)
DepSatSpec015Model000	1858	2192,036 s (~36 min)	1811,398 s (~30 min)

Conclusion

We measured that we had an overall 9,8 % increase in number of POs discharged compared to the previous version. A extra time of more than few minutes has been observed for discharge the POs. This result should be interpret with caution, probably some provers discharged the sequent simplified by the new version of the GenMP reasoner.