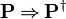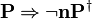Variations in HYP, CNTR and GenMP: Difference between revisions
imported>Laurent |
imported>Josselin fix misleading descriptions |
||
| Line 24: | Line 24: | ||
== Variation Implementation == | == Variation Implementation == | ||
In order to simplify and optimize the generation of variation of the sought predicate, 4 functions (common to HYP, HYP_OR, CNTR and GenMP reasoners) have been implemented. | In order to simplify and optimize the generation of variation of the sought predicate, 4 functions (common to HYP, HYP_OR, CNTR and GenMP reasoners) have been implemented. Each function takes as input a predicate and returns a list of predicates generated by applying their corresponding rule. | ||
These functions have been defined as follows: | These functions have been defined as follows: | ||
* StongerPositive(P) = <math>\{Q | * StongerPositive(P) = <math>\{Q \mid Q \limp P\} \;\; (\lnot P \limp \lnot Q)</math> | ||
* WeakerPositive(P) = <math>\{Q | * WeakerPositive(P) = <math>\{Q \mid P \limp Q\} \;\; (\lnot Q \limp \lnot P )</math> | ||
* StongerNegative(P) = <math>\{Q | * StongerNegative(P) = <math>\{Q \mid Q \limp \lnot P\} \;\; (P \limp \lnot Q)</math> | ||
* WeakerNegative(P) = <math>\{Q | * WeakerNegative(P) = <math>\{Q \mid \lnot P \limp Q\} \;\; (\lnot Q \limp P )</math> | ||
A rule can be written in 2 implications, one for each sign of the predicate P. | |||
Some optimisations, to reduce the number of implication to implement, have been implemented. Indeed, only the implications <math>(Q \limp P, P \limp Q, P \limp \lnot Q, \lnot Q \limp P)</math> have been implemented because they cover all cases. For instance, if the function StongerPositive takes a negative predicate as an input, the function returns a list of predicates stronger (e.g which infer) than the input. But it's also performed by the function StongerNegative. So this function applies the predicate negation and call to StongerNegative function. | |||
Note: | Note: | ||
These functions assume the operators such as '<math>\neq</math>' have been removed by the normalization. Moreover, as explained in the convention part, the list of predicates returned contains only | These functions assume the operators such as '<math>\neq</math>' have been removed by the normalization. Moreover, as explained in the convention part, the list of predicates returned contains only predicates in a normal form. | ||
== Reasoners Implementation == | == Reasoners Implementation == | ||
=== HYP, HYP_OR === | === HYP, HYP_OR === | ||
The HYP reasoner generates a list of | The HYP reasoner calls to StongerPositive function in order to generates a list of predicates that infer the goal (or disjunct). Thus, the sequent is discharged iff at least one hypothesis is contained into this list. | ||
The HYP_OR reasoner | The HYP_OR reasoner proceeds the same, for each disjunct a list of stronger predicates is generated and then the sequent is dicharged if at least one hypothesis is contained into these lists. | ||
=== CNTR === | === CNTR === | ||
Checks if the predicate | Checks if the predicate, that we would contradict, is not null and it is contained into the hypotheses. | ||
If the | If the given predicate is a positive predicate, it generates a list of predicates which infer the predicate. Else, it splits a conjunctive hypothesis if necessary into its conjuncts and compute for each conjunct a list of predicates wich infer the negation of the predicate (or conjunct). Finally, it saves into the list named neededHyps the hypotheses contained into the lists previously computed (hypotheses which contradict the given hypothesis). | ||
=== GEN_MP === | === GEN_MP === | ||
First, it extracts all predicates (unless predicates <math> \btrue and \bfalse</math>) from the hypotheses. For each hypothesis its computes: | First, it extracts all predicates (unless predicates <math> \btrue and \bfalse</math>) from the hypotheses. For each hypothesis its computes: | ||
* a list of | * a list of predicates which could be remplaced by <math> \btrue </math> and which are weaker than the hypothesis. | ||
* a list of | * a list of predicates which could be remplaced by <math> \bfalse </math> and which are stronger than the negation of the hypothesis. | ||
Then, it extracts the goal or the disjuncts if the sequent contain a goal in a disjunctive form. For each predicate its computes: | Then, it extracts the goal or the disjuncts if the sequent contain a goal in a disjunctive form. For each predicate its computes: | ||
* a list of | * a list of predicates which could be remplaced by <math> \bfalse </math> and which are stronger than the hypothesis. | ||
* a list of | * a list of predicates which could be remplaced by <math> \btrue </math> and which are weaker than the negation of the hypothesis. | ||
| Line 70: | Line 68: | ||
* the substitue <math> ( \btrue / \bfalse ) </math> | * the substitue <math> ( \btrue / \bfalse ) </math> | ||
In order to simplify predicate | In order to simplify predicate searching algorithm (avoid sign distinction), the sub-predicate should be positive. | ||
Afterwards, each predicate extracted from hypotheses or the goal is traversed to get the list of possible applications of substitutes while ensuring that a given predicate could'nt be rewritten by himself. | Afterwards, each predicate extracted from hypotheses or the goal is traversed to get the list of possible applications of substitutes while ensuring that a given predicate could'nt be rewritten by himself. | ||
A possible applications of substitutes corresponds to a position into the predicate to rewrite and a sustitute. | A possible applications of substitutes corresponds to a position into the predicate to rewrite and a sustitute. | ||
Finally, the goal is re-written using the applications of substitutes computed | Finally, the goal is re-written using the applications of substitutes computed. Thus, the re-written goal and the hypotheses needed to achieve it are stored. Then the hypotheses are re-written by producing new hypothesis actions. | ||
'''Note''': This improvement corresponds to the level 2 of GenMP. | '''Note''': This improvement corresponds to the level 2 of GenMP. | ||
| Line 124: | Line 122: | ||
First, it checks that the program argument is a directory and then it imports all Rodin projects from the directory into a workspace. The Auto-prover is applied on all Rodin | First, it checks that the program argument is a directory and then it imports all Rodin projects from the directory into a workspace. The Auto-prover is applied on all Rodin projects. For each Rodin project the following informations are displayed : "Project: Number of POs discharged/Number of POs". Finally, the proof files are strored into a directory named "Results" at the same level as the directory where is contained the Rodin projects. | ||
== Tests == | == Tests == | ||
| Line 469: | Line 467: | ||
== Conclusion == | == Conclusion == | ||
We measured that we had an overall 9,8 % increase in number of POs discharged compared to the previous version. | We measured that we had an overall 9,8 % increase in number of POs discharged compared to the previous version. | ||
A | A less time of few minutes has been observed for discharge the POs. Only one time measurement have been taken into account because the others are too short. Moreover, this result is not really significiant because even if the new version discharges more sequent than the previous, it decharges earlier than the previous version. | ||
Revision as of 14:30, 21 November 2013
This page describes the introduction of variations in the HYP, HYP_OR, CNTR and GENMP reasoners.
Context
The reasoners implementing the inference rules
,
,
and
look for exact matches of a predicate. But, quite often, a similar predicate that does not match exactly (e.g., because it has been normalized) would suffice. There is also the possibility that a variation which is equivalent to the predicate would be present. For instance, "¬ a = b" is equivalent to "¬ b = a". Finally, the reasoners shall also consider variations which are a sufficient condition for the rule. For instance, if the goal is "a ≤ b", then a hypothesis "a < b" is a sufficient condition to discharge the goal with
.
Objective
The point of this enhancement is therefore to increase the proof power of the considered reasoners by having them consider variations of the sought predicate.
Conventions
The variations in the Inference Rules page have been generated such that the following facts hold:
Moreover, we consider only variations that are in normal form (that is invariant under rewriting by the auto-rewriter of the sequent prover). This is why the table does not contain predicates such as 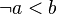 , but contain
, but contain 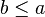 instead.
instead.
Implementation
This section explains how the variation have been implemented.
Variation Implementation
In order to simplify and optimize the generation of variation of the sought predicate, 4 functions (common to HYP, HYP_OR, CNTR and GenMP reasoners) have been implemented. Each function takes as input a predicate and returns a list of predicates generated by applying their corresponding rule.
These functions have been defined as follows:
- StongerPositive(P) =
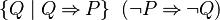
- WeakerPositive(P) =
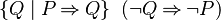
- StongerNegative(P) =
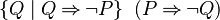
- WeakerNegative(P) =
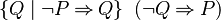
A rule can be written in 2 implications, one for each sign of the predicate P.
Some optimisations, to reduce the number of implication to implement, have been implemented. Indeed, only the implications 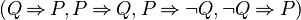 have been implemented because they cover all cases. For instance, if the function StongerPositive takes a negative predicate as an input, the function returns a list of predicates stronger (e.g which infer) than the input. But it's also performed by the function StongerNegative. So this function applies the predicate negation and call to StongerNegative function.
have been implemented because they cover all cases. For instance, if the function StongerPositive takes a negative predicate as an input, the function returns a list of predicates stronger (e.g which infer) than the input. But it's also performed by the function StongerNegative. So this function applies the predicate negation and call to StongerNegative function.
Note:
These functions assume the operators such as '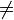 ' have been removed by the normalization. Moreover, as explained in the convention part, the list of predicates returned contains only predicates in a normal form.
' have been removed by the normalization. Moreover, as explained in the convention part, the list of predicates returned contains only predicates in a normal form.
Reasoners Implementation
HYP, HYP_OR
The HYP reasoner calls to StongerPositive function in order to generates a list of predicates that infer the goal (or disjunct). Thus, the sequent is discharged iff at least one hypothesis is contained into this list.
The HYP_OR reasoner proceeds the same, for each disjunct a list of stronger predicates is generated and then the sequent is dicharged if at least one hypothesis is contained into these lists.
CNTR
Checks if the predicate, that we would contradict, is not null and it is contained into the hypotheses.
If the given predicate is a positive predicate, it generates a list of predicates which infer the predicate. Else, it splits a conjunctive hypothesis if necessary into its conjuncts and compute for each conjunct a list of predicates wich infer the negation of the predicate (or conjunct). Finally, it saves into the list named neededHyps the hypotheses contained into the lists previously computed (hypotheses which contradict the given hypothesis).
GEN_MP
First, it extracts all predicates (unless predicates  ) from the hypotheses. For each hypothesis its computes:
) from the hypotheses. For each hypothesis its computes:
- a list of predicates which could be remplaced by
 and which are weaker than the hypothesis.
and which are weaker than the hypothesis. - a list of predicates which could be remplaced by
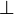 and which are stronger than the negation of the hypothesis.
and which are stronger than the negation of the hypothesis.
Then, it extracts the goal or the disjuncts if the sequent contain a goal in a disjunctive form. For each predicate its computes:
- a list of predicates which could be remplaced by
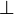 and which are stronger than the hypothesis.
and which are stronger than the hypothesis. - a list of predicates which could be remplaced by
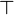 and which are weaker than the negation of the hypothesis.
and which are weaker than the negation of the hypothesis.
For each substitution computed the following informations are stored:
- predicate original (hypothesis or goal)
- a boolean tells if the substitution comes from the goal
- the sub-predicate to substitute
- the substitue
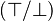
In order to simplify predicate searching algorithm (avoid sign distinction), the sub-predicate should be positive.
Afterwards, each predicate extracted from hypotheses or the goal is traversed to get the list of possible applications of substitutes while ensuring that a given predicate could'nt be rewritten by himself. A possible applications of substitutes corresponds to a position into the predicate to rewrite and a sustitute.
Finally, the goal is re-written using the applications of substitutes computed. Thus, the re-written goal and the hypotheses needed to achieve it are stored. Then the hypotheses are re-written by producing new hypothesis actions.
Note: This improvement corresponds to the level 2 of GenMP.
Performances
Configuration
System:
- Intel(R) Core(TM) i7-4770 CPU @ (8* 3.40GHz)
- 24 Go RAM
OS:
- Ubuntu 12.04.3 LTS
- linux kernel 3.5.0-43
Java:
- java-7-openjdk-i386
- VM arguments
- -Xms512m
- -Xmx1024m
Eclipse:
- Indigo (3.7.2)
Benchmark Projects
The Rodin projects have been taken from the Deploy archives.
Protocol
A measurement is launched using the plug-in org.eventb.seqprover.core.perf.app. Tests are run from a launched eclipse application.
Launch Configuration must include exactly the following plug-ins:
- org.eventb.core
- org.eventb.core.seqprover
- org.eventb.core.ast
- org.rodinp.core
- org.eventb.core.seqprover.core.per.app
Add the following program argument:
- -application org.eventb.smt.core.perf.app.main <project-dir>
where <project-dir> is the path of the directory where is contained the Rodin projects.
Verify that 1024 Mo are free when tests are ready for launch.
First, it checks that the program argument is a directory and then it imports all Rodin projects from the directory into a workspace. The Auto-prover is applied on all Rodin projects. For each Rodin project the following informations are displayed : "Project: Number of POs discharged/Number of POs". Finally, the proof files are strored into a directory named "Results" at the same level as the directory where is contained the Rodin projects.
Tests
- Previous version : commit 69e0ae43a1
- New version : commit 2ea1cf6ffe
Results
The following results are averages of measures on the Auto-prover
| Projects | Number Of POs | Number Of POs discharged (previous version) | Number Of POs discharged (new version) |
|---|---|---|---|
| Doors | 108 | 24 | 24 |
| ssf | 60 | 11 | 11 |
| ch915_rev | 31 | 9 | 9 |
| Celebrity | 46 | 11 | 11 |
| search_backward | 31 | 8 | 8 |
| ch916_doors | 103 | 26 | 26 |
| B2B_mini_pilot_080806 | 498 | 272 | 280 |
| DynamicStableLSR_090624 | 390 | 171 | 171 |
| SimpleLyra | 55 | 33 | 33 |
| paper_pomc | 85 | 29 | 30 |
| ch7_conc | 248 | 152 | 155 |
| ch912_mobile | 153 | 57 | 57 |
| routing_new | 241 | 86 | 86 |
| ch915_inv | 32 | 17 | 18 |
| FloodSet | 244 | 102 | 103 |
| Rabin-110907 | 209 | 70 | 70 |
| DSAOCSSv003 | 90 | 35 | 35 |
| ch917_train | 133 | 49 | 49 |
| CDIS | 91 | 40 | 40 |
| Zer_ess | 55 | 27 | 27 |
| search_proved | 31 | 10 | 10 |
| mode_su_12 | 439 | 366 | 382 |
| search | 31 | 10 | 10 |
| Club-120130 | 57 | 21 | 22 |
| ch2_car | 237 | 143 | 168 |
| Cowboy-110905 | 16 | 9 | 9 |
| ch915_mini | 25 | 5 | 5 |
| society_sol | 9 | 0 | 0 |
| gcd | 175 | 105 | 105 |
| pattern_poor | 88 | 69 | 70 |
| ch913_ieee | 67 | 21 | 21 |
| A2A_081216 | 276 | 161 | 168 |
| ch910_ring | 28 | 8 | 8 |
| HermanRing-110906 | 58 | 24 | 24 |
| ch911_tree | 81 | 34 | 36 |
| BoschSwitch | 19 | 9 | 9 |
| ch4_brp | 127 | 83 | 86 |
| ProofMethod-130117 | 14 | 4 | 4 |
| ch915_bin | 37 | 12 | 13 |
| ParkingLot | 10 | 4 | 4 |
| Galois | 1 | 0 | 0 |
| ch915_search | 17 | 10 | 10 |
| ch915_sqrt | 17 | 9 | 9 |
| ch915_sort | 67 | 25 | 25 |
| society | 7 | 0 | 0 |
| BepiColombo_Models_v6.4 | 155 | 90 | 90 |
| proof_obligations | 39 | 18 | 18 |
| DepSatSpec015Model000 | 1858 | 672 | 1300 |
| ch6_brp | 149 | 100 | 103 |
| press | 60 | 42 | 54 |
| SSF_minipilot | 24 | 6 | 6 |
| ch4_file_1 | 52 | 21 | 21 |
| SignalControl-110527 | 135 | 88 | 93 |
| ResponseCoalitionNormative | 178 | 40 | 40 |
| ch8_circ_arbiter | 153 | 114 | 128 |
| pattern_rich | 128 | 112 | 112 |
| Modes_v2 | 121 | 50 | 50 |
| DiningCryptSpec-100406 | 24 | 15 | 15 |
| Mini_doors | 12 | 4 | 4 |
| ResponseCoalitionPerturbed | 227 | 42 | 42 |
| family_sol | 9 | 1 | 1 |
| Total | 7683 | 3564 | 3914 |
| Projects | Number Of POs | Time (previous version) | Time (new version) |
|---|---|---|---|
| DepSatSpec015Model000 | 1858 | 2192,036 s (~36 min) | 1811,398 s (~30 min) |
Conclusion
We measured that we had an overall 9,8 % increase in number of POs discharged compared to the previous version. A less time of few minutes has been observed for discharge the POs. Only one time measurement have been taken into account because the others are too short. Moreover, this result is not really significiant because even if the new version discharges more sequent than the previous, it decharges earlier than the previous version.