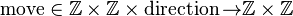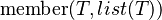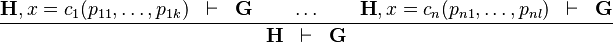Datatype Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Nicolas m New page: Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer. They applied to the following datatypes: Directions: direct... |
imported>Nicolas m corrected typos |
||
| Line 1: | Line 1: | ||
Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer. | Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer. | ||
== Datatypes used == | |||
The rules will be applied to the following datatypes: | |||
Directions: | Directions: | ||
| Line 11: | Line 13: | ||
| west | | west | ||
Let | Let us have a function | ||
<math>\operatorname{move} | <math>\operatorname{move} \in \Z \cprod \Z \cprod \operatorname{direction} \tfun \Z \cprod \Z </math> | ||
first two arguments are a start position, third is a direction, result is the end position. | first two arguments are a start position, third is a direction, result is the end position. | ||
| Line 18: | Line 20: | ||
Lists: | Lists: | ||
list( | list(T) ::= | ||
nil | nil | ||
| cons( head : | | cons( head : T, tail : list(T) ) | ||
Let | Let us have a predicate | ||
<math>\operatorname{member}( | <math>\operatorname{member}(T, list(T))</math> | ||
meaning that the first argument is a member of the list. | meaning that the first argument is a member of the list. | ||
| Line 29: | Line 31: | ||
Trees: | Trees: | ||
tree( | tree(T) ::= | ||
empty | empty | ||
| node( left : tree( | | node( left : tree(T), value : T, right : tree(T) ) | ||
Let <math>\operatorname{height} | Let us have a function | ||
<math>\operatorname{height} \in \operatorname{Tree} \tfun \N</math> defining the height of a tree | |||
== Distinct Case == | == Distinct Case == | ||
Revision as of 16:23, 6 September 2010
Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer.
Datatypes used
The rules will be applied to the following datatypes:
Directions:
direction ::=
north
| east
| south
| west
Let us have a function
first two arguments are a start position, third is a direction, result is the end position.
Lists:
list(T) ::=
nil
| cons( head : T, tail : list(T) )
Let us have a predicate
meaning that the first argument is a member of the list.
Trees:
tree(T) ::= empty | node( left : tree(T), value : T, right : tree(T) )
Let us have a function
defining the height of a tree
Distinct Case
The rule states
Application to directions
TODO
!x,y,dir . move(x,y,dir) /= x |-> y
Application to lists
TODO
!l oftype list(\Z). #x. member(x,l) & (!y. member(y,l) => y <= x)
evidence that nil list has been forgotten in the predicate
Application to trees
TODO
Induction
TODO