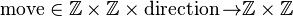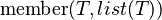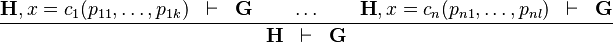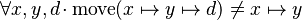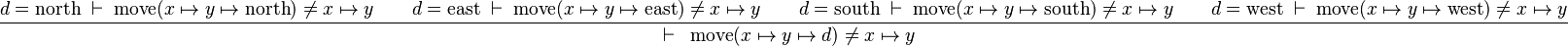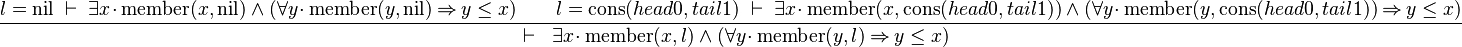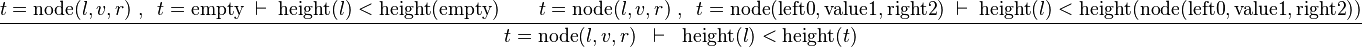Datatype Rules: Difference between revisions
imported>Nicolas |
imported>Nicolas mNo edit summary |
||
| Line 52: | Line 52: | ||
<math>\forall x,y,d \qdot \operatorname{move}(x \mapsto y \mapsto d) \neq x \mapsto y</math> | <math>\forall x,y,d \qdot \operatorname{move}(x \mapsto y \mapsto d) \neq x \mapsto y</math> | ||
we can free variables x,y,d then apply Distinct Case: | we can free variables x,y,d then apply Distinct Case on d: | ||
The resulting proof step is | The resulting proof step is | ||
| Line 73: | Line 73: | ||
=== Application to trees === | === Application to trees === | ||
{{ | Starting from goal | ||
<math>\forall l,v,r,t. t = \operatorname{node}(l,v,r) \limp \operatorname{height}(l) < \operatorname{height}(t)</math> | |||
we can free variables l,v,r,t then apply IMP_R and then Distinct Case on t: | |||
<math>\frac{ t = \operatorname{node}(l,v,r) \;,\;\; t=\operatorname{empty} \;\vdash \; \operatorname{height}(l) < \operatorname{height}(\operatorname{empty}) \qquad t = \operatorname{node}(l,v,r) \;,\;\; t = \operatorname{node}(\operatorname{left0},\operatorname{value1},\operatorname{right2}) \;\vdash \; \operatorname{height}(l) < \operatorname{height}(\operatorname{node}(\operatorname{left0},\operatorname{value1},\operatorname{right2})) }{ t = \operatorname{node}(l,v,r) \;\;\vdash\;\; \operatorname{height}(l) < \operatorname{height}(t) }</math> | |||
== Induction == | == Induction == | ||
{{TODO}} | {{TODO}} | ||
Revision as of 17:15, 6 September 2010
Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer.
Datatypes used
The rules will be applied to the following datatypes:
Directions:
direction ::=
north
| east
| south
| west
Let us have a function
first two arguments are a start position, third is a direction, result is the end position.
Lists:
list(T) ::=
nil
| cons( head : T, tail : list(T) )
Let us have a predicate
meaning that the first argument is a member of the list.
Trees:
tree(T) ::= empty | node( left : tree(T), value : T, right : tree(T) )
Let us have a function
defining the height of a tree
Distinct Case
The rule states
Application to directions
Starting from goal
we can free variables x,y,d then apply Distinct Case on d:
The resulting proof step is
further simplifications depend on the existence of rules about move and the various directions.
Application to lists
Starting from goal
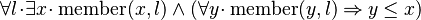
we can free variable l then apply Distinct Case on it:
The left antecedent shows that the case of the nil list has been forgotten when writing the theorem.
Application to trees
Starting from goal
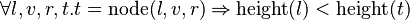
we can free variables l,v,r,t then apply IMP_R and then Distinct Case on t:
Induction
TODO