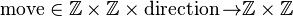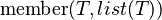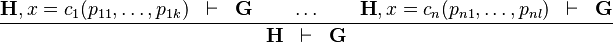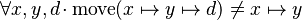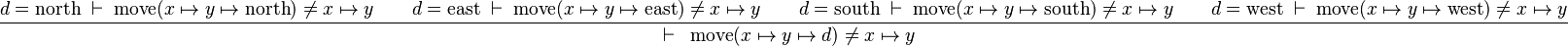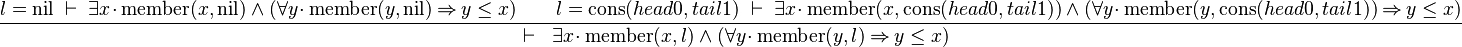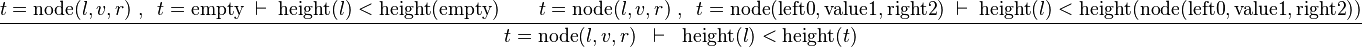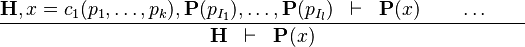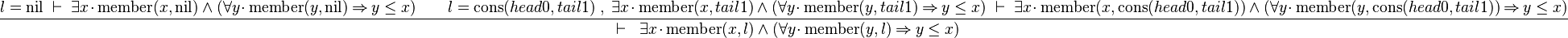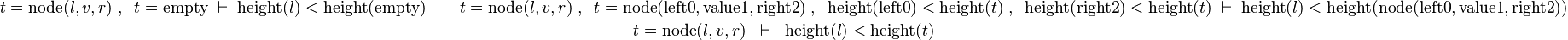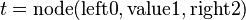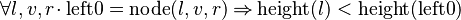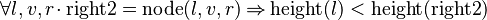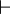Datatype Rules: Difference between revisions
imported>Nicolas |
imported>Nicolas Induction |
||
| Line 85: | Line 85: | ||
== Induction == | == Induction == | ||
{{ | The rule states | ||
<math>\frac{ \textbf{H}, x=c_1(p_1, \ldots, p_k),\textbf{P}(p_{I_1}), \ldots, \textbf{P}(p_{I_l}) \;\;\vdash \;\; \textbf{P}(x) \qquad \ldots \qquad}{ \textbf{H} \;\;\vdash\;\; \textbf{P}(x) }</math> | |||
The only difference with Distinct Case resides in the <math>\textbf{P}(p_{I_1}), \ldots, \textbf{P}(p_{I_l})</math> hypotheses for inductive parameters. | |||
=== Application to directions === | |||
Starting from goal | |||
<math>\forall x,y,d \qdot \operatorname{move}(x \mapsto y \mapsto d) \neq x \mapsto y</math> | |||
we can free variables x,y,d then apply Induction on d: | |||
The resulting proof step is | |||
<math>\frac{ d=\operatorname{north} \;\vdash \; \operatorname{move}(x \mapsto y \mapsto \operatorname{north}) \neq x \mapsto y \qquad d=\operatorname{east} \;\vdash \; \operatorname{move}(x \mapsto y \mapsto \operatorname{east}) \neq x \mapsto y \qquad d=\operatorname{south} \;\vdash \; \operatorname{move}(x \mapsto y \mapsto \operatorname{south}) \neq x \mapsto y \qquad d=\operatorname{west} \;\vdash \; \operatorname{move}(x \mapsto y \mapsto \operatorname{west}) \neq x \mapsto y }{ \;\;\vdash\;\; \operatorname{move}(x \mapsto y \mapsto d) \neq x \mapsto y }</math> | |||
As we can see, it is exactly the same proof step as for Distinct Case: the reason is that the direction constructors contain no parameters, a fortiori no inductive parameters, so there are no additional hypotheses. | |||
=== Application to lists === | |||
Starting from goal | |||
<math>\forall l \qdot \exists x \qdot \operatorname{member}(x,l) \land (\forall y \qdot \operatorname{member}(y,l) \limp y \leq x)</math> | |||
we can free variable l then apply Induction on it: | |||
<math>\frac{ l=\operatorname{nil} \;\vdash \; \exists x \qdot \operatorname{member}(x,\operatorname{nil}) \land (\forall y \qdot \operatorname{member}(y,\operatorname{nil}) \limp y \leq x) \qquad l=\operatorname{cons}(head0, tail1) \;,\; \exists x \qdot \operatorname{member}(x,tail1) \land (\forall y \qdot \operatorname{member}(y,tail1) \limp y \leq x) \;\vdash \; \exists x \qdot \operatorname{member}(x,\operatorname{cons}(head0, tail1)) \land (\forall y \qdot \operatorname{member}(y,\operatorname{cons}(head0, tail1)) \limp y \leq x) }{ \;\;\vdash\;\; \exists x \qdot \operatorname{member}(x,l) \land (\forall y \qdot \operatorname{member}(y,l) \limp y \leq x) }</math> | |||
The left antecedent shows the same problem as Distinct for nil list. The benefit of the Induction is in the right antecedent with the additional hypothesis that the predicate stands for tail1. Next step will be to free the x in the tail1 hypothesis, then use it to instantiate the x in the goal with <math>\operatorname{max}(\operatorname{head0}, x_{\operatorname{tail1}})</math>. | |||
In this proof, application of Distinct Case does not allow to complete the proof (at least not so easily), whereas Induction does. | |||
=== Application to trees === | |||
Starting from goal | |||
<math>\forall l,v,r,t \qdot t = \operatorname{node}(l,v,r) \limp \operatorname{height}(l) < \operatorname{height}(t)</math> | |||
we can free variables l,v,r,t then apply IMP_R and then Induction on t: | |||
<math>\frac{ t = \operatorname{node}(l,v,r) \;,\;\; t=\operatorname{empty} \;\vdash \; \operatorname{height}(l) < \operatorname{height}(\operatorname{empty}) \qquad t = \operatorname{node}(l,v,r) \;,\;\; t = \operatorname{node}(\operatorname{left0},\operatorname{value1},\operatorname{right2}) \;,\;\; \operatorname{height}(\operatorname{left0}) < \operatorname{height}(t) \;,\;\; \operatorname{height}(\operatorname{right2}) < \operatorname{height}(t) \;\vdash \; \operatorname{height}(l) < \operatorname{height}(\operatorname{node}(\operatorname{left0},\operatorname{value1},\operatorname{right2})) }{ t = \operatorname{node}(l,v,r) \;\;\vdash\;\; \operatorname{height}(l) < \operatorname{height}(t) }</math> | |||
the left antecedent will then be proved using the contradiction in hypotheses. In the right one, additional induction hypotheses do not provide much help: we are in a situation very similar to the one after applying Distinct Case. It can be more appropriate to free only the t variable, then apply induction to the whole predicate: <math>\forall l,v,r \qdot t = \operatorname{node}(l,v,r) \limp \operatorname{height}(l) < \operatorname{height}(t)</math> | |||
that gives the following right antecedent: | |||
<math>t = \operatorname{node}(\operatorname{left0},\operatorname{value1},\operatorname{right2})</math> | |||
<math>\forall l,v,r \qdot \operatorname{left0} = \operatorname{node}(l,v,r) \limp \operatorname{height}(l) < \operatorname{height}(\operatorname{left0})</math> | |||
<math>\forall l,v,r \qdot \operatorname{right2} = \operatorname{node}(l,v,r) \limp \operatorname{height}(l) < \operatorname{height}(\operatorname{right2})</math> | |||
<math>\vdash</math> | |||
<math>\forall l,v,r \qdot t = \operatorname{node}(l,v,r) \limp \operatorname{height}(l) < \operatorname{height}(t)</math> | |||
Revision as of 11:48, 7 September 2010
Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer.
Datatypes used
The rules will be applied to the following datatypes:
Directions:
direction ::=
north
| east
| south
| west
Let us have a function
first two arguments are a start position, third is a direction, result is the end position.
Lists:
list(T) ::=
nil
| cons( head : T, tail : list(T) )
Let us have a predicate
meaning that the first argument is a member of the list.
Trees:
tree(T) ::= empty | node( left : tree(T), value : T, right : tree(T) )
Let us have a function
defining the height of a tree
Distinct Case
The rule states
Application to directions
Starting from goal
we can free variables x,y,d then apply Distinct Case on d:
The resulting proof step is
further simplifications depend on the existence of rules about move and the various directions.
Application to lists
Starting from goal
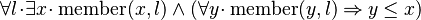
we can free variable l then apply Distinct Case on it:
The left antecedent shows that the case of the nil list has been forgotten when writing the theorem.
Application to trees
Starting from goal
we can free variables l,v,r,t then apply IMP_R and then Distinct Case on t:
the left antecedent will then be proved using the contradiction in hypotheses. The right one will require eh on t in hypotheses and SIMP_EQUAL_CONSTR, then properties about height.
Induction
The rule states
The only difference with Distinct Case resides in the 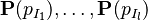 hypotheses for inductive parameters.
hypotheses for inductive parameters.
Application to directions
Starting from goal
we can free variables x,y,d then apply Induction on d:
The resulting proof step is
As we can see, it is exactly the same proof step as for Distinct Case: the reason is that the direction constructors contain no parameters, a fortiori no inductive parameters, so there are no additional hypotheses.
Application to lists
Starting from goal
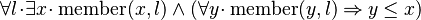
we can free variable l then apply Induction on it:
The left antecedent shows the same problem as Distinct for nil list. The benefit of the Induction is in the right antecedent with the additional hypothesis that the predicate stands for tail1. Next step will be to free the x in the tail1 hypothesis, then use it to instantiate the x in the goal with 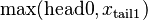 .
In this proof, application of Distinct Case does not allow to complete the proof (at least not so easily), whereas Induction does.
.
In this proof, application of Distinct Case does not allow to complete the proof (at least not so easily), whereas Induction does.
Application to trees
Starting from goal
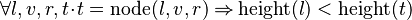
we can free variables l,v,r,t then apply IMP_R and then Induction on t:
the left antecedent will then be proved using the contradiction in hypotheses. In the right one, additional induction hypotheses do not provide much help: we are in a situation very similar to the one after applying Distinct Case. It can be more appropriate to free only the t variable, then apply induction to the whole predicate: 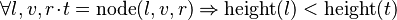
that gives the following right antecedent: