Generic Instantiation: Difference between revisions
imported>Son |
imported>Laurent mNo edit summary |
||
| Line 4: | Line 4: | ||
== Issues: Instantiation of Carrier Sets == | == Issues: Instantiation of Carrier Sets == | ||
Currently, the proposal mentions that the carrier sets can be instantiated | Currently, the proposal mentions that the carrier sets can be instantiated with any set expressions (which contains existing carrier sets and constants). Besides the declared axioms in the development to be extended there are two ''hidden'' axioms for every carrier set <math>S</math>: | ||
<math> S \neq \emptyset</math> | <math> S \neq \emptyset</math> | ||
| Line 12: | Line 12: | ||
Both these axioms can be generated as theorems in the instantiating context which need to be proved. | Both these axioms can be generated as theorems in the instantiating context which need to be proved. | ||
However, the second theorem can be proved if <math>S</math> is instantiated | However, the second theorem can be proved only if <math>S</math> is instantiated with a type expression. | ||
This could be a limitation of generic instantiation (<font color=red>Son: Is this a real limitation? To be discussed</font>) and may restrict the applicability of the approach. One should allow carrier sets to be instantiated | This could be a limitation of generic instantiation (<font color=red>Son: Is this a real limitation? To be discussed</font>) and may restrict the applicability of the approach. One should allow carrier sets to be instantiated with some set expressions which are not necessary carrier sets themselves. | ||
The issue, here is that this will definitely introduce unsoundness into the instantiation process. Examples include when formula which are no longer well-defined; and/or the meaning operator such <code>id</code> or <code>prj1</code>, <code>prj2</code> has been changed (<font color=red>Son: Maybe some examples are needed</font>). | The issue, here is that this will definitely introduce unsoundness into the instantiation process. Examples include when formula which are no longer well-defined; and/or the meaning operator such <code>id</code> or <code>prj1</code>, <code>prj2</code> has been changed (<font color=red>Son: Maybe some examples are needed</font>). | ||
[[Category:Design proposal]] | [[Category:Design proposal]] | ||
Revision as of 12:54, 31 March 2010
The initial proposal from Southampton is as follows. File:Proposal generic instantiation rodin.pdf.
Issues: Instantiation of Carrier Sets
Currently, the proposal mentions that the carrier sets can be instantiated with any set expressions (which contains existing carrier sets and constants). Besides the declared axioms in the development to be extended there are two hidden axioms for every carrier set  :
:
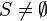
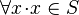
Both these axioms can be generated as theorems in the instantiating context which need to be proved.
However, the second theorem can be proved only if  is instantiated with a type expression.
is instantiated with a type expression.
This could be a limitation of generic instantiation (Son: Is this a real limitation? To be discussed) and may restrict the applicability of the approach. One should allow carrier sets to be instantiated with some set expressions which are not necessary carrier sets themselves.
The issue, here is that this will definitely introduce unsoundness into the instantiation process. Examples include when formula which are no longer well-defined; and/or the meaning operator such id or prj1, prj2 has been changed (Son: Maybe some examples are needed).