Induction proof: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Christophe New page: This page explains how to proove with induction method on the natural number with Rodin tools. In other words, how to proove :<br/> <math> P(0) </math><br/> <math> \forall i.i \in \mathbb{... |
imported>Christophe No edit summary |
||
| Line 11: | Line 11: | ||
</math><br/> | </math><br/> | ||
<math>\forall i. i \in \mathbb{N} \Rightarrow P(i+1)</math> | <math>\forall i. i \in \mathbb{N} \Rightarrow P(i+1)</math> | ||
---- | |||
The proof key is the following theorem:<br/> | |||
<math> | |||
\forall s.s \subseteq \mathbb{N} \land 0 \in s \land (\forall n.n \in s => n+1 \in s)\Rightarrow N \subseteq s | |||
Revision as of 21:06, 13 October 2008
This page explains how to proove with induction method on the natural number with Rodin tools.
In other words, how to proove :
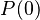
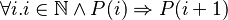
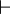
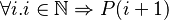
The proof key is the following theorem:
<math>
\forall s.s \subseteq \mathbb{N} \land 0 \in s \land (\forall n.n \in s => n+1 \in s)\Rightarrow N \subseteq s