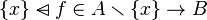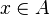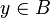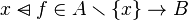Maplet Overriding in Goal: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Billaude |
imported>Billaude |
||
| Line 10: | Line 10: | ||
= Design Decision = | = Design Decision = | ||
Instead of proofing the first sub-goal, it may be more easy to proof <math>f\in A\to B</math> which is a sufficient condition : <math>(f\in A\to B)\limp ({x} \domsub f \in A \smallsetminus | Instead of proofing the first sub-goal, it may be more easy to proof <math>f\in A\to B</math> which is a sufficient condition : <math>(f\in A\to B)\limp (\{x\} \domsub f \in A \smallsetminus \{x\} \to B)</math>. | ||
= Implementation = | = Implementation = | ||
Revision as of 13:09, 30 May 2011
This page describes the design of a tactic requested here : Feature Request #3306228
Objective
Split every goal in the form : 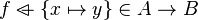 into three sub-goals :
into three sub-goals :
Design Decision
Instead of proofing the first sub-goal, it may be more easy to proof 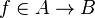 which is a sufficient condition :
which is a sufficient condition : 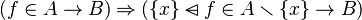 .
.
Implementation
First, the goal is checked. Its tree structure must match the following one :
├──
│ ├── f │ └── {} │ └──
│ ├── x │ └── y └──
├── A └── B
Then, if the hypothesis 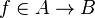 is contained in the hypothesis the goal is splitted as follows :
is contained in the hypothesis the goal is splitted as follows :
Else, it is splitted as follows :