Membership in Goal: Difference between revisions
imported>Billaude |
imported>Billaude Not finished |
||
| Line 2: | Line 2: | ||
This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.<br> | This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.<br> | ||
This reasoner discharges sequent whose goal denotes a membership which can be inferred | This reasoner discharges sequent whose goal denotes a membership which can be inferred from hypotheses. Here an basic example of what it discharges :<br> | ||
<math>H,\quad x\in S,\quad S\subset T,\quad T\subseteq U \quad\vdash x\in U</math> | <math>H,\quad x\in S,\quad S\subset T,\quad T\subseteq U \quad\vdash x\in U</math> | ||
| Line 15: | Line 15: | ||
Such a reasoner contributes to prove more Proof Obligations automatically, faster and with fewer needed hypotheses which makes proof rule more legible and proof replay less sensitive to modifications. | Such a reasoner contributes to prove more Proof Obligations automatically, faster and with fewer needed hypotheses which makes proof rule more legible and proof replay less sensitive to modifications. | ||
= Tactic = | = Design Decision = | ||
== Tactic == | |||
This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working. | This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working. | ||
== Goal == | === Goal === | ||
The tactic (as the reasoner) should works only on goals such as : | The tactic (as the reasoner) should works only on goals such as : | ||
*<math> | *<math>\cdots~\in~\cdots</math> | ||
For examples : | |||
For | |||
*<math>f(x)\in g\otimes h</math> | *<math>f(x)\in g\otimes h</math> | ||
*<math>x\in A\cprod\left(B\cup C\right)</math> | *<math>x\in A\cprod\left(B\cup C\right)</math> | ||
*<math>x\mapsto y\in A\cprod B</math> | |||
== Hypotheses == | In the latter case, the reasoner won't try to prove that ''x'' belongs to ''A'' and ''y'' belongs to ''B'', but that the mapplet belong to the Cartesian product. | ||
=== Hypotheses === | |||
Now we have to find hypotheses leading to discharge the sequent. To do so, the tactic recovers two kinds of hypotheses : | |||
#the ones related to the left member of the goal <math>\left( x\in S\right)</math> (this is the start point): | #the ones related to the left member of the goal <math>\left( x\in S\right)</math> (this is the start point): | ||
#*<math>x\in \cdots</math> | #*<math>x\in \cdots</math> | ||
#*<math>\cdots\mapsto x\mapsto\cdots\in\cdots</math> | #*<math>\cdots\mapsto x\mapsto\cdots\in\cdots</math> | ||
#*<math>\left\{\cdots, x,\cdots\right\}\ | #*<math>\left\{\cdots, x,\cdots\right\}=\cdots</math> | ||
#*<math>\left\{\cdots, \cdots\mapsto x\mapsto\cdots,\cdots\right\}=\cdots</math> | |||
#the ones denoting inclusion (all but the ones matching the description of the first point) : | #the ones denoting inclusion (all but the ones matching the description of the first point) : | ||
#*<math>\cdots\subset\cdots</math> | #*<math>\cdots\subset\cdots</math> | ||
#*<math>\cdots\subseteq\cdots</math> | #*<math>\cdots\subseteq\cdots</math> | ||
#*<math>\cdots=\cdots</math> | |||
#*<math> | |||
Then, it will search a link between those hypotheses so that the sequent can be discharged. | Then, it will search a link between those hypotheses so that the sequent can be discharged. | ||
== Find a path == | === Find a path === | ||
Now that we recovered all the hypotheses that could be useful for the reasoner, it | Now that we recovered all the hypotheses that could be useful for the reasoner, it remains to find a path among the hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. <math>f</math> always represent an expression (may be a domain, a range, etc.). | ||
#The following sequent is provable because <math>f\subseteq \varphi (f)</math>. | #The following sequent is provable because <math>f\subseteq \varphi (f)</math>. | ||
#*<math>x\in f,\quad \varphi (f)\subseteq g\quad\vdash\quad x\in g</math> | #*<math>x\in f,\quad \varphi (f)\subseteq g\quad\vdash\quad x\in g</math> | ||
| Line 52: | Line 50: | ||
#We can generalized the first two points. This is the Russian dolls system. We can easily prove a sequent with multiple inclusions by going from hypothesis to hypothesis. | #We can generalized the first two points. This is the Russian dolls system. We can easily prove a sequent with multiple inclusions by going from hypothesis to hypothesis. | ||
#*<math>x\in \psi (f),\quad \varphi (f)\subseteq g\quad\vdash\quad x\in g</math> | #*<math>x\in \psi (f),\quad \varphi (f)\subseteq g\quad\vdash\quad x\in g</math> | ||
#For some relations, | #For some relations, [[#positions|positions]] are needed to be known to continue to find hypotheses, but it is not always necessary. | ||
#*<math>x\mapsto y\in f,\quad f\subseteq A\cprod B\quad\vdash\quad x\in A</math> | #*<math>x\mapsto y\in f,\quad f\subseteq A\cprod B\quad\vdash\quad x\in A</math> | ||
#*<math>x\in dom(f),\quad f\subseteq A\cprod B\quad\vdash\quad x\in A</math> | #*<math>x\in dom(f),\quad f\subseteq A\cprod B\quad\vdash\quad x\in A</math> | ||
| Line 58: | Line 56: | ||
#*<math>x\in f,\quad f\otimes g\subseteq A\cprod\left(B\cprod C\right)\quad\vdash\quad x\in A\cprod B</math> | #*<math>x\in f,\quad f\otimes g\subseteq A\cprod\left(B\cprod C\right)\quad\vdash\quad x\in A\cprod B</math> | ||
#*<math>x\in f,\quad f\parallel g\subseteq \left(A\cprod C\right)\cprod\left(B\cprod D\right)\quad\vdash\quad x\in A\cprod B</math> | #*<math>x\in f,\quad f\parallel g\subseteq \left(A\cprod C\right)\cprod\left(B\cprod D\right)\quad\vdash\quad x\in A\cprod B</math> | ||
#Those rewrites can be useful | #Those rewrites can be useful. They should be implemented in the auto-rewriter later. | ||
#*<math>dom(f)\cup dom(g) = dom(f\ovl g)</math> | #*<math>dom(f)\cup dom(g) = dom(f\ovl g)</math> | ||
#*<math>ran(f)\cup ran(g)\subseteq ran(f\ovl g)</math> | #*<math>ran(f)\cup ran(g)\subseteq ran(f\ovl g)</math> | ||
#*<math>dom(A\domres f) = dom(f)\cap A</math> | #*<math>dom(A\domres f) = dom(f)\cap A</math> | ||
#*<math>ran(f\ranres A) = ran(f)\cap A</math> | #*<math>ran(f\ranres A) = ran(f)\cap A</math> | ||
By using these inclusion and rewrites, it tries to find a path among the recovered hypotheses. Every | By using these inclusion and rewrites, it tries to find a path among the recovered hypotheses. Every one of those should only be used once, avoiding possible infinite loop <math>\left(A\subseteq B,\quad B\subseteq A\right)</math>. Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input. | ||
== Reasoner == | |||
The way the reasoner must work is still in discussion. | |||
= Implementation = | |||
This section explain how the tactic has bee implemented. | |||
=== Positions === | |||
As it was said, we may sometimes need the position. It is represented by an array of integer. Here are the possible values the array contains (atomic positions) : | |||
* '''''kdom''''' : it corresponds to the domain. | |||
**<math>\left[A\cprod B\right]_{pos\;=\;kdom} = A</math> | |||
**<math>\left[x\mapsto y\right]_{pos\;=\;kdom} = x</math> | |||
**<math>\left[g\right]_{pos\;=\;kdom} = dom(g)</math> | |||
* '''''kran''''' : it corresponds to the domain. | |||
**<math>\left[A\cprod B\right]_{pos\;=\;kran} = B</math> | |||
**<math>\left[x\mapsto y\right]_{pos\;=\;kran} = y</math> | |||
**<math>\left[g\right]_{pos\;=\;kran} = ran(g)</math> | |||
* '''''leftDProd''''' : it corresponds to the left member of a direct product. | |||
**<math>\left[f\otimes g\right]_{pos\;=\;leftDProd} = f</math> | |||
**<math>\left[A\cprod \left(B\cprod C\right)\right]_{pos\;=\;leftDProd} = A\cprod B</math> | |||
* '''''rightDProd''''' : it corresponds to the right member of a direct product | |||
**<math>\left[f\otimes g\right]_{pos\;=\;rightDProd} = g</math> | |||
**<math>\left[A\cprod\left(B\cprod C\right)\right]_{pos\;=\;rightDProd} = A\cprod C</math> | |||
* '''''leftPProd''''' : it corresponds to the left member of a parallel product | |||
**<math>\left[f\parallel g\right]_{pos\;=\;leftPProd} = f</math> | |||
**<math>\left[\left(A\cprod B\right)\cprod\left(C\cprod D\right)\right]_{pos\;=\;leftPProd} = A\cprod C</math> | |||
* '''''rightPProd''''' : it corresponds to the right member of a parallel product | |||
**<math>\left[f\parallel g\right]_{pos\;=\;rightPProd} = g</math> | |||
**<math>\left[\left(A\cprod B\right)\cprod\left(C\cprod D\right)\right]_{pos\;=\;rightPProd} = B\cprod D</math> | |||
* '''''converse''''' : it corresponds to the child of an inverse | |||
**<math>\left[f^{-1}\right]_{pos\;=\;converse}=f</math> | |||
**<math>\left[A\cprod B\right]_{pos\;=\;converse} = B\cprod A</math> | |||
For example, the following expressions at the given positions are equivalent. | |||
:<math>\left[f\otimes\left(\left(A\cprod dom(g)\right)\parallel g\right)\right]_{pos\;=\;\left[rightDProd,\;leftPProd,\;kran\right]} = \left[\left(A\cprod dom(g)\right)\parallel g\right]_{pos\;=\;\left[leftPProd,\;kran\right]} = \left[A\cprod dom(g)\right]_{pos\;=\;\left[kran\right]} = \left[dom(g)\right]_{pos\;=\;\left[~\right]} = \left[g\right]_{pos\;=\;\left[kdom\right]}</math> | |||
Some combinations of atomic positions are equivalent. In order to simplify comparison between positions, they are normalized : | |||
*<math>ran(f^{-1}) = dom(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kran\right]} = \left[f\right]_{pos\;=\;\left[kdom\right]}</math> | |||
*<math>dom(f^{-1}) = ran(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kdom\right]} = \left[f\right]_{pos\;=\;\left[kran\right]}</math> | |||
*<math>\left(f^{-1}\right)^{-1} = f\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~converse\right]} = \left[f\right]_{pos\;=\;\left[~\right]}</math> | |||
=== Goal === | |||
As explained in the design decision part, goal is checked. If it matches the description here above <math>\left(x\in S\right)</math> then ''x'' is stored in an attribute. Moreover, from the set ''S'', we compute every pair ''expression'' & ''position'' equivalent to it. For example, from the set <math>dom(ran(ran(g)))</math>, the map will be computed : | |||
*<math>dom(ran(ran(g)))\;\mapsto\;[\;]</math> | |||
*<math>ran(ran(g))\;\mapsto\;[0]</math> | |||
*<math>ran(g)\;\mapsto\;[1,~0]</math> | |||
*<math>g\;\mapsto\;[1,~1,~0]</math> | |||
Only ''range'', ''domain'' and ''converse'' can be taken into account to get all the possibles goals. | |||
A pair (expression ; position) is said equal to the goal if and only if there exists a pair equivalent to the goal (GoalExp ; GoalPos) and a pair equivalent to the given pair (Exp ; Pos) such as ''Pos = GoalPos'' and ''Exp'' is contained in ''GoalExp''. | |||
=== Hypotheses === | |||
As explained in the design decision part, there are two kinds of hypotheses which are recovered. But when hypotheses related to the left member of the goal <math>\left(x\in S\right)</math> are stored, the position of ''x'' is also record. Then, if there is an hypothesis such as <math>\left\{\cdots\;,\;y\mapsto x\mapsto z\;,\;m\mapsto x\;,\;\cdots\right\} = A</math>, then this hypothesis is mapped to the positions <math>\left\{\left[0,~1\right],~\left[1\right]\right\}</math>. | |||
= | === Find a path === | ||
Let's considered the sequent with the following goal : <math>x\in V</math>. | |||
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position <math>pos</math> and the set <math>S</math> as explained in [[#Hypotheses|hypotheses]]. Then, for each equivalent pair to these one <math>\left(S', pos'\right)</math>, we compute set containing <math>S'</math> ([[#Design Decision#Tactic#Find a path| Find a path 2.]]). For every new pair, we test if it is contained in the goal. | |||
To be continued. | |||
== | = Untreated cases = | ||
Some cases are not treated. Further enhancement may be provided for some. | |||
*<math>x\in A\cup B,\quad A\cup B\cup C\subseteq D\quad\vdash\quad x\in D</math> | |||
*<math>x\in f,\quad f\in A\;op\;B\quad\vdash\quad x\in A\cprod B</math> | |||
*<math>f\ovl \left\{x\mapsto y\right\}\subseteq A\cprod B\quad\vdash\quad x\in A</math> | |||
*<math>x\in f\otimes g,\quad f\subseteq A\cprod B,\quad g\subseteq C\cprod D\quad\vdash\quad x\in (A\cprod C)\cprod(B\cprod D)</math> | |||
*<math>x\in f\otimes g,\quad f\subseteq h\quad\vdash\quad x\in h\otimes g</math> | |||
*<math>x\in \left\{a,~b,~c\right\},\quad\left\{a,~b,~c,~d,~e,~f\right\}\subseteq D\quad\vdash\quad x\in D</math> | |||
*<math>x\in A\cprod B,\quad A\subseteq C\quad\vdash\quad x\in C\cprod B</math> | |||
*<math>x\in dom(f)\cap A\quad\vdash\quad x\in dom(A\domres f)</math> | |||
*<math>x\in ran(f)\cap A\quad\vdash\quad x\in ran(f\ranres A)</math> | |||
*<math>x\in \quad\vdash\quad</math> | |||
*<math>\quad\vdash\quad</math> | |||
*<math>\quad\vdash\quad</math> | |||
*<math>\quad\vdash\quad</math> | |||
*:<math>\bigl(</math> where <math>op_1</math> and <math>op_2</math> are ones of :<math>\quad\rel, \trel, \srel, \strel, \pfun, \tfun, \pinj, \tinj, \psur, \tsur, \tbij\bigr)</math> | |||
[[Category:Design proposal]] | [[Category:Design proposal]] | ||
Revision as of 16:23, 13 July 2011
Objective
This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.
This reasoner discharges sequent whose goal denotes a membership which can be inferred from hypotheses. Here an basic example of what it discharges :
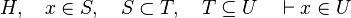
Analysis
Such sequent are proved by PP and ML. But, these provers have both drawbacks :
- All the visible are added as needed hypotheses, which is most of the time not the case.
- They take quite consequent time to prove it (even with the basic example given here above, the difference in time execution is noticeable).
- If there are too many hypotheses, or if the expression of the
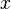 is too complicated, they may not prove it.
is too complicated, they may not prove it.
This is particularly true when in the list of inclusion expressions of each side of the relation are not equal. For example : 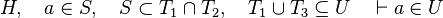
Such a reasoner contributes to prove more Proof Obligations automatically, faster and with fewer needed hypotheses which makes proof rule more legible and proof replay less sensitive to modifications.
Design Decision
Tactic
This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working.
Goal
The tactic (as the reasoner) should works only on goals such as :
For examples :
In the latter case, the reasoner won't try to prove that x belongs to A and y belongs to B, but that the mapplet belong to the Cartesian product.
Hypotheses
Now we have to find hypotheses leading to discharge the sequent. To do so, the tactic recovers two kinds of hypotheses :
- the ones related to the left member of the goal
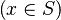 (this is the start point):
(this is the start point):
- the ones denoting inclusion (all but the ones matching the description of the first point) :
Then, it will search a link between those hypotheses so that the sequent can be discharged.
Find a path
Now that we recovered all the hypotheses that could be useful for the reasoner, it remains to find a path among the hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. 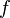 always represent an expression (may be a domain, a range, etc.).
always represent an expression (may be a domain, a range, etc.).
- The following sequent is provable because
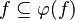 .
.
- The following sequent is provable because
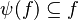 .
.
- We can generalized the first two points. This is the Russian dolls system. We can easily prove a sequent with multiple inclusions by going from hypothesis to hypothesis.
- For some relations, positions are needed to be known to continue to find hypotheses, but it is not always necessary.
- Those rewrites can be useful. They should be implemented in the auto-rewriter later.
By using these inclusion and rewrites, it tries to find a path among the recovered hypotheses. Every one of those should only be used once, avoiding possible infinite loop  . Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
. Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
Reasoner
The way the reasoner must work is still in discussion.
Implementation
This section explain how the tactic has bee implemented.
Positions
As it was said, we may sometimes need the position. It is represented by an array of integer. Here are the possible values the array contains (atomic positions) :
- kdom : it corresponds to the domain.
- kran : it corresponds to the domain.
- leftDProd : it corresponds to the left member of a direct product.
- rightDProd : it corresponds to the right member of a direct product
- leftPProd : it corresponds to the left member of a parallel product
- rightPProd : it corresponds to the right member of a parallel product
- converse : it corresponds to the child of an inverse
For example, the following expressions at the given positions are equivalent.
Some combinations of atomic positions are equivalent. In order to simplify comparison between positions, they are normalized :
Goal
As explained in the design decision part, goal is checked. If it matches the description here above 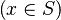 then x is stored in an attribute. Moreover, from the set S, we compute every pair expression & position equivalent to it. For example, from the set
then x is stored in an attribute. Moreover, from the set S, we compute every pair expression & position equivalent to it. For example, from the set 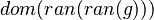 , the map will be computed :
, the map will be computed :
Only range, domain and converse can be taken into account to get all the possibles goals.
A pair (expression ; position) is said equal to the goal if and only if there exists a pair equivalent to the goal (GoalExp ; GoalPos) and a pair equivalent to the given pair (Exp ; Pos) such as Pos = GoalPos and Exp is contained in GoalExp.
Hypotheses
As explained in the design decision part, there are two kinds of hypotheses which are recovered. But when hypotheses related to the left member of the goal 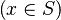 are stored, the position of x is also record. Then, if there is an hypothesis such as
are stored, the position of x is also record. Then, if there is an hypothesis such as 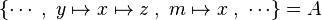 , then this hypothesis is mapped to the positions
, then this hypothesis is mapped to the positions ![\left\{\left[0,~1\right],~\left[1\right]\right\}](/images/math/9/8/f/98f4b25272ac46fc08b6f57cec71d01a.png) .
.
Find a path
Let's considered the sequent with the following goal : 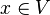 .
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position
.
We start with the hypotheses which have a connection with the goal's member. Such a hypothesis gives two informations : the position 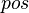 and the set
and the set  as explained in hypotheses. Then, for each equivalent pair to these one
as explained in hypotheses. Then, for each equivalent pair to these one 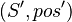 , we compute set containing
, we compute set containing 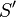 ( Find a path 2.). For every new pair, we test if it is contained in the goal.
( Find a path 2.). For every new pair, we test if it is contained in the goal.
To be continued.
Untreated cases
Some cases are not treated. Further enhancement may be provided for some.
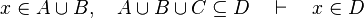
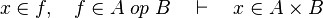
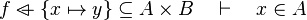
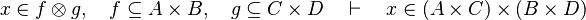
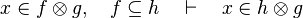
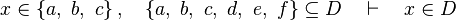
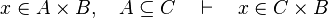
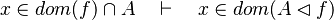
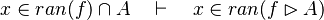
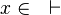
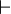
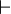
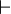
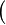 where
where 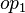 and
and 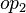 are ones of :
are ones of :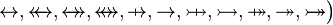
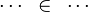
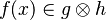
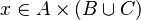
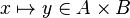
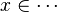
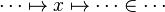
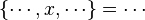
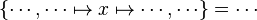
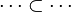
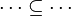

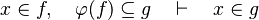

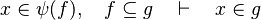

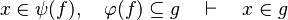
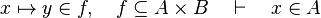
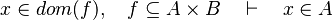
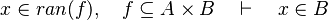
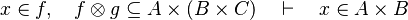
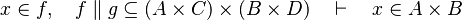
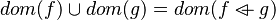
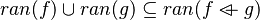
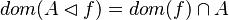
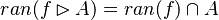
![\left[A\cprod B\right]_{pos\;=\;kdom} = A](/images/math/5/c/9/5c9188384893a5f785386fd9be5f5211.png)
![\left[x\mapsto y\right]_{pos\;=\;kdom} = x](/images/math/2/0/2/202d5f1c44ca4d283d912b36a0363bdb.png)
![\left[g\right]_{pos\;=\;kdom} = dom(g)](/images/math/9/e/8/9e8243fbfbf64a5fbf4dd9c86a803249.png)
![\left[A\cprod B\right]_{pos\;=\;kran} = B](/images/math/5/1/e/51e9dde2c7714a18994bfd88133abaff.png)
![\left[x\mapsto y\right]_{pos\;=\;kran} = y](/images/math/a/f/9/af9a897a8826985891b874f9b9909e12.png)
![\left[g\right]_{pos\;=\;kran} = ran(g)](/images/math/7/f/1/7f1b4c4c2ce799142d20e081fab53cff.png)
![\left[f\otimes g\right]_{pos\;=\;leftDProd} = f](/images/math/b/0/a/b0a7f686b54248608ecf9c73ce1f3817.png)
![\left[A\cprod \left(B\cprod C\right)\right]_{pos\;=\;leftDProd} = A\cprod B](/images/math/e/0/5/e0590d93e6fdc6af17c1506a5ee7d15a.png)
![\left[f\otimes g\right]_{pos\;=\;rightDProd} = g](/images/math/3/3/0/33035f3ff4539e1277b11829a42ee95e.png)
![\left[A\cprod\left(B\cprod C\right)\right]_{pos\;=\;rightDProd} = A\cprod C](/images/math/2/9/7/297b727d53b54bb89f7f17a4f5334dce.png)
![\left[f\parallel g\right]_{pos\;=\;leftPProd} = f](/images/math/e/6/e/e6ef9f8e373f62db6106d9ef438303cc.png)
![\left[\left(A\cprod B\right)\cprod\left(C\cprod D\right)\right]_{pos\;=\;leftPProd} = A\cprod C](/images/math/e/5/a/e5a91f7dc4c558594d9fe98efbe475ce.png)
![\left[f\parallel g\right]_{pos\;=\;rightPProd} = g](/images/math/8/4/b/84b62af850f72686cef3794e2a1857c6.png)
![\left[\left(A\cprod B\right)\cprod\left(C\cprod D\right)\right]_{pos\;=\;rightPProd} = B\cprod D](/images/math/2/8/7/28711556277dec142585edf1f933d101.png)
![\left[f^{-1}\right]_{pos\;=\;converse}=f](/images/math/f/6/d/f6d099908d10e496857d491b0ee6bca9.png)
![\left[A\cprod B\right]_{pos\;=\;converse} = B\cprod A](/images/math/5/5/8/5580559f9c30df0338362d5a49c66335.png)
![\left[f\otimes\left(\left(A\cprod dom(g)\right)\parallel g\right)\right]_{pos\;=\;\left[rightDProd,\;leftPProd,\;kran\right]} = \left[\left(A\cprod dom(g)\right)\parallel g\right]_{pos\;=\;\left[leftPProd,\;kran\right]} = \left[A\cprod dom(g)\right]_{pos\;=\;\left[kran\right]} = \left[dom(g)\right]_{pos\;=\;\left[~\right]} = \left[g\right]_{pos\;=\;\left[kdom\right]}](/images/math/a/e/2/ae2f4629684baa99b2a77a1f9f027513.png)
![ran(f^{-1}) = dom(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kran\right]} = \left[f\right]_{pos\;=\;\left[kdom\right]}](/images/math/9/a/b/9ab2c57a971be9093b74331cfdf365f2.png)
![dom(f^{-1}) = ran(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kdom\right]} = \left[f\right]_{pos\;=\;\left[kran\right]}](/images/math/d/1/4/d145100f50452d20541cbc2113d8a9c4.png)
![\left(f^{-1}\right)^{-1} = f\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~converse\right]} = \left[f\right]_{pos\;=\;\left[~\right]}](/images/math/f/f/2/ff2fe24f0d2d75efe4839f2d2bfe2130.png)
![dom(ran(ran(g)))\;\mapsto\;[\;]](/images/math/8/9/6/896c9400150a21f66969511b65b17aff.png)
![ran(ran(g))\;\mapsto\;[0]](/images/math/9/1/f/91f6448f76145edbc41623b7e45e8873.png)
![ran(g)\;\mapsto\;[1,~0]](/images/math/d/0/5/d05c506a68faeaf5c449140bbc6e88ef.png)
![g\;\mapsto\;[1,~1,~0]](/images/math/7/0/f/70fc39947ec6c685617c07e4d641629a.png)