Adding Reasoners(How to extend Rodin Tutorial): Difference between revisions
imported>Tommy mNo edit summary |
imported>Tommy mNo edit summary |
||
| Line 4: | Line 4: | ||
Rodin support several provers. Some are embedded such as NewPP, or the sequent prover which will talk about here, and some are added through plug-ins (as the Atelier B provers : ML, PP, P0, etc). | Rodin support several provers. Some are embedded such as NewPP, or the sequent prover which will talk about here, and some are added through plug-ins (as the Atelier B provers : ML, PP, P0, etc). | ||
Contributing to Rodin sequent prover is done by adding tactics. These tactics | Contributing to Rodin sequent prover is done by adding tactics. These tactics which often involve a set of reasoners, apply on proof tree nodes. The reasoners apply on the sequent of a given proof tree node. A reasoner is (and has to be) quite "rough" : it shall take a given sequent and produce a proof rule that will (if possible) apply on this given sequent, whereas a tactic could be smarter. Indeed, a tactic can involve several reasoners, thus apply them in loops, and combine them, or even call other tactics. A tactic can be either automatic (auto tactic and/or post tactic) or manual (using providers in the UI that paint their applications in red on formulas) in case of interactive proof.<br> | ||
A reasoner encapsulates a kind of "proof step", also called "proof rule". The sequent prover provides a set of tactics applying proof rules (and other tactics). These rules are either rewriting rules (see [[All_Rewrite_Rules|rewriting | A reasoner encapsulates a kind of "proof step", also called "proof rule". The sequent prover provides a set of tactics applying proof rules (and even other tactics!). These rules are either rewriting rules (see [[All_Rewrite_Rules|rewriting rule list]]) or inference rules (see [[Inference_Rules|inference rule list]]). It is actually a really critical piece of code, that developers should understand at first sight, and be convinced about its correctness. If one codes a wrong reasoner, one breaks the whole soundness of proofs done within Rodin! As they are written in pure java, and accorded to the previous considerations, they have to be the simpliest and most readable as possible. Finally, it is needed to write tests that cover all the possible cases of application of one given reasoner (this will not be detailed in this tutorial). | ||
=== In this part === | === In this part === | ||
In this part we will see how to contribute to the sequent prover of Rodin by encapsulating a new proof rule within a reasoner and add a tactic to the sequent prover of Rodin that will encapsulate this reasoner. | In this part we will see how to contribute to the sequent prover of Rodin by encapsulating a new proof rule within a reasoner and add a tactic to the sequent prover of Rodin that will encapsulate this reasoner. | ||
The rule we want to apply is the following: | The rule, coded within the reasoner, that we want to apply is the following: | ||
<math>\frac{ \textbf{H},\; a = b \;\; \vdash \;\; \textbf{G}} {\textbf{H},\; a \leq b,\;b \leq a\;\vdash \;\; \textbf{G}}</math> | {| cellpadding="20" cellspacing="0" border="1" | ||
|<math>\frac{ \textbf{H},\; a = b \;\; \vdash \;\; \textbf{G}} {\textbf{H},\; a \leq b,\;b \leq a\;\vdash \;\; \textbf{G}}</math> | |||
| DBL_INEQ | |||
|} | |||
Let's call this rule DBL_INEQ. By reading this rule, we see it is goal agnostic. This means that the rule will be applied if the prover sequent under consideration contains the hypotheses <math>a \leq b,\;b \leq a</math>, whatever the goal of this sequent. | |||
=== Step1 === | |||
=== Step2 === | === Step2 === | ||
Revision as of 11:39, 27 September 2010
Principles
Rodin support several provers. Some are embedded such as NewPP, or the sequent prover which will talk about here, and some are added through plug-ins (as the Atelier B provers : ML, PP, P0, etc).
Contributing to Rodin sequent prover is done by adding tactics. These tactics which often involve a set of reasoners, apply on proof tree nodes. The reasoners apply on the sequent of a given proof tree node. A reasoner is (and has to be) quite "rough" : it shall take a given sequent and produce a proof rule that will (if possible) apply on this given sequent, whereas a tactic could be smarter. Indeed, a tactic can involve several reasoners, thus apply them in loops, and combine them, or even call other tactics. A tactic can be either automatic (auto tactic and/or post tactic) or manual (using providers in the UI that paint their applications in red on formulas) in case of interactive proof.
A reasoner encapsulates a kind of "proof step", also called "proof rule". The sequent prover provides a set of tactics applying proof rules (and even other tactics!). These rules are either rewriting rules (see rewriting rule list) or inference rules (see inference rule list). It is actually a really critical piece of code, that developers should understand at first sight, and be convinced about its correctness. If one codes a wrong reasoner, one breaks the whole soundness of proofs done within Rodin! As they are written in pure java, and accorded to the previous considerations, they have to be the simpliest and most readable as possible. Finally, it is needed to write tests that cover all the possible cases of application of one given reasoner (this will not be detailed in this tutorial).
In this part
In this part we will see how to contribute to the sequent prover of Rodin by encapsulating a new proof rule within a reasoner and add a tactic to the sequent prover of Rodin that will encapsulate this reasoner. The rule, coded within the reasoner, that we want to apply is the following:
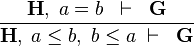
|
DBL_INEQ |
Let's call this rule DBL_INEQ. By reading this rule, we see it is goal agnostic. This means that the rule will be applied if the prover sequent under consideration contains the hypotheses 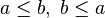 , whatever the goal of this sequent.
, whatever the goal of this sequent.