Adding Reasoners(How to extend Rodin Tutorial)

<prev: Generating the proof obligations

^up: How to extend Rodin Tutorial (Index)

Principles

Rodin support several provers. Some are embedded such as NewPP, or the sequent prover which will talk about here, and some are added by external plug-ins (as the Atelier B provers : ML, PP, P0, etc).

Contributing to Rodin sequent prover is done by adding tactics. These tactics which often involve a set of reasoners, apply on proof tree nodes. The reasoners apply on the sequent of a given proof tree node. A reasoner is (and has to be) quite "rough" : it shall take a given sequent and produce a proof rule that will (if possible) apply on this given sequent, whereas a tactic could be smarter. Indeed, a tactic can involve several reasoners, thus apply them in loops, and combine them, or even call other tactics. A tactic can be either automatic (auto tactic and/or post tactic) or manual (using providers in the UI that paint their applications in red on formulas) in case of interactive proof.

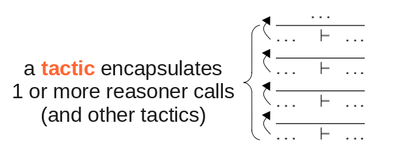
A reasoner encapsulates a kind of "proof step", also called "proof rule". The sequent prover provides a set of tactics applying proof rules (and even other tactics!). These rules are either rewriting rules (see rewriting rule list) or inference rules (see inference rule list). It is actually a really critical piece of code, that developers should understand at first sight, and be convinced about its correctness. If one codes a wrong reasoner, one breaks the whole soundness of proofs done within Rodin! As they are written in pure java, and accorded to the previous considerations, they have to be the simpliest and most readable as possible. Finally, it is needed to write tests that cover all the possible cases of application of one given reasoner (this will not be detailed in this tutorial).

In this part

In this part we will see how to contribute to the sequent prover of Rodin by encapsulating a new proof rule within a reasoner and add a tactic to the sequent prover of Rodin that will encapsulate this reasoner. The rule, coded within the reasoner, that we want to apply is the following:

$\frac{ \textbf{H},\; a = b \;\; \vdash \;\; \textbf{G}} {\textbf{H},\; a \leq b,\;b \leq a\;\vdash \;\; \textbf{G}}$

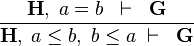
DBL_INEQ

Let's call this rule DBL_INEQ. By reading this rule, we see it is goal agnostic. This means that the rule will be applied if the prover sequent under consideration contains the hypotheses 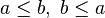$a \leq b,\;b \leq a$, whatever the goal of this sequent. We will say that 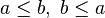$a \leq b,\;b \leq a$ are the "Needed hypotheses".

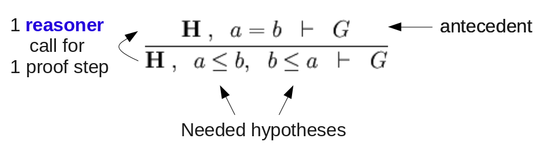
Moreover, 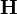$\textbf{H}$ is the set of selected hypotheses from the input sequent, and 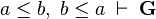$a \leq b,\;b \leq a\;\vdash \;\textbf{G}$ is the antecedent of the rule (i.e. a child node to be proved).

Step1

• Create a new plugin that will host our reasoner and tactic. It will not be any activator for this plug-in but the option "Activate this plug-in when one of its classes is loaded" shall be selected.
• Create a new class for the reasoner, called DoubleInequalityReasoner.

Step2

Implement the body of the reasoner :

• the reasoner shall "implements IVersionedReasoner" thus getVersion() shall return a static integer giving the current version of our reasoner. 0 might not be a wrong choice for our first try. getReasonerID() shall return a unique ID that we will further use when registering our reasoner extension point in our plugin. Create here something like :

private static final String REASONER_ID = "org.eventb.doubleInequality.dblIneq";

You should now have something close to this :

public class DoubleInequalityReasoner implements IVersionedReasoner {

	private static final int VERSION = 0;
	private static final String REASONER_ID = "org.eventb.doubleInequality.dblIneq";

	@Override
	public String getReasonerID() {
		return REASONER_ID;
	}

	@Override
	public int getVersion() {
		return VERSION;
	}

	@Override
	public IReasonerOutput apply(IProverSequent seq, IReasonerInput input,
			IProofMonitor pm) {

       }

Step3 / Exercise

Implement the method public IReasonerOutput apply(IProverSequent seq, IReasonerInput input, IProofMonitor pm). This method is where one shall create the proof rule to be applied from the input sequent seq and with the given input if needed. Here is the list of tasks you have to perform in this apply() method :

• get and check the input predicate a <= b,
• check the presence of the other hypothesis b <= a,
• make the new hypothesis a=b that will be in the antecedent produced by our rule,
• make the antecedent (see the picture above) where a <= b and b <= a are deselected(i.e. hidden) so that the tactic does not apply in unfinite loop,
• make the proof rule to return,

Step4

Here we see together the solution proposed for the implementation of the apply() method of our reasoner:

@Override
public IReasonerOutput apply(IProverSequent seq, IReasonerInput input, IProofMonitor pm) {

• get and check the input predicate a <= b

NB : Here we suppose that the given input doesn't have any error. If it has, we shall return a reasonerFailure(See ProverFactory.reasonerFailure() method for more details).
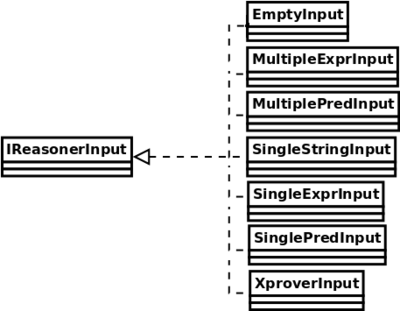
We want our IReasonerInput to be a predicate input of the form "a <= b". Thus, there is an existing class to reuse : SinglePredInput.
Please, have a look at IReasonerInput implementation hierarchy to see which kind of input classes exist and that you could reuse in your reasoners.

Thus, here is what you should write :

  if (input.hasError()) {
    return ProverFactory.reasonerFailure(this, input, input.getError());
  }
  final SinglePredInput predInput = (SinglePredInput) input;
  final Predicate predicate = predInput.getPredicate();
  if (predicate.getTag() != Formula.LE) {
    return ProverFactory.reasonerFailure(this, input, "invalid input predicate");
  }

• check the presence of the other hypothesis b <= a

  // we are sure that the predicate is a relational predicate as we checked that getTag() == Formula.LE
  final RelationalPredicate aLEb = (RelationalPredicate) predicate;
  final Expression a = aLEb.getLeft();
  final Expression b = aLEb.getRight();
  final FormulaFactory ff = seq.getFormulaFactory(); // we retrieve the formula factory 
  final Predicate bLEa = ff.makeRelationalPredicate(Formula.LE, b, a,	null); // we build b <= a
  if (!seq.containsHypotheses(Arrays.asList(aLEb, bLEa))) {
    return ProverFactory.reasonerFailure(this, input,"sequent does not contain required hypotheses");
  }

• make the new hypothesis a=b

NB : we reuse the formula factory that we got from the sequent to create the new hypothesis a = b :

  final Predicate aEqb = ff.makeRelationalPredicate(Formula.EQUAL, a, b, null);

• make the antecedent

  // we create the added hypothesis a = b
  final Set<Predicate> addedHyps = Collections.singleton(aEqb);
  // we hide a <= b and b <= a
  final ISelectionHypAction hideIneqs = ProverFactory.makeHideHypAction(Arrays.asList(aLEb, bLEa));
  // we create our antecedent to be used in our proof rule
  final IAntecedent antecedent = ProverFactory.makeAntecedent(null, addedHyps, hideIneqs);

• make the proof rule to return

  // We do not forget to say that a <= b (aLEb) and b <= a (bLEa) are needed for our rule to be applied
  final Set<Predicate> neededHyps = new HashSet<Predicate>();
  neededHyps.addAll(Arrays.asList(aLEb, bLEa));

  // We return the proof rule corresponding to DBL_INEQ
  return ProverFactory.makeProofRule(this, input, null, neededHyps, "Inequality Rewrites", antecedent);

 }

Step5

As our input is actually a SinglePredInput, which as its name describes, holds a predicate, our reasoner is actually an specialisation of the abstract class SinglePredInputReasoner. Please check the other proposed (e.g. published) types of reasoners corresponding to existing inputs among :

• SingleExprInputReasoner,
• SinglePredInputReasoner,
• SingleStringInputReasoner,
• EmptyInputReasoner,
• ForwardInfReasoner,
• HypothesisReasoner,
• XProverInputReasoner.

In our case, simply add the extends SinglePredInputReasoner to the declaration of the reasoner class. And this is all for our reasoner! Now let's add a tactic corresponding to it.

Step6

Now that we have the reasoner DoubleInequalityReasoner, we need to create a tactic to call this reasoner when possible. So what we have to do is creating a tactic (e.g. that implements ITactic) which will calculate if the current proof tree node contains an application of the reasoner, and if it is the case, call the reasoner.

To do so... create the tactic class DoubleInequalityTactic which implements ITactic. You can see that the only method to implement is : apply(IProofTreeNode ptNode, IProofMonitor pm) We will detail here, what one should do in this method:

@Override
public Object apply(IProofTreeNode ptNode, IProofMonitor pm) {

• First, we search for double inequalities a <= b and b <= a in the selected hypotheses. To search it, we traverse all the selected hypotheses via sequent.selectedHypIterable() then when we encounter one hypothesis of the form E <= F (e.g. hypothesis.getTag() == Formula.LE) then we build the hypothesis F <= E and if the sequent contains this latter hypothesis, we call the reasoner DoubleInequalityReasoner.

final IProverSequent sequent = ptNode.getSequent();
final FormulaFactory ff = sequent.getFormulaFactory();
  for (Predicate hyp : sequent.selectedHypIterable()) {

• when we encounter one hypothesis of the form E <= F (e.g. hypothesis.getTag() == Formula.LE), then we build the hypothesis F <= E :

	if (hyp.getTag() == Formula.LE) {
		final RelationalPredicate aLEb = (RelationalPredicate) hyp;
		final Expression a = aLEb.getLeft();
		final Expression b = aLEb.getRight();
		final RelationalPredicate bLEa = ff.makeRelationalPredicate(Formula.LE, b, a, null);

• if the sequent contains this latter hypothesis, we call the reasoner DoubleInequalityReasoner (encapsulated in a tactic)

		if(sequent.containsHypothesis(bLEa)) {
                	return callDblIneqReasoner(ptNode, aLEb, pm);
 		}
	}
 }
 return "no double inequality hypotheses found";
}

As we need to construct the SinglePredInput with the hypothesis a <= b, and then apply our reasoner, the usual way to do this, is to encapsulate this reasoner call into a tactic. There is a facility to do that offered by BasicTactics.reasonerTac. Thus we write the following :

1  private Object callDblIneqReasoner(IProofTreeNode ptNode, final RelationalPredicate inputPred, IProofMonitor pm) {
2   final ITactic dblIneqTac = BasicTactics.reasonerTac(new DoubleInequalityReasoner(), new SinglePredInput(inputPred));
3   return dblIneqTac.apply(ptNode, pm);
4  }

where at line 2 we encapsulate the reasoner call, and at line 3, we apply the reasoner.

<prev: Generating the proof obligations

^up: How to extend Rodin Tutorial (Index)