Set Rewrite Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Benoit Added rule SIMP_FINITE_BOOL. |
imported>Benoit Removed rules SIMP_SPECIAL_FORALL_BTRUE, SIMP_SPECIAL_FORALL_BFALSE, SIMP_SPECIAL_EXISTS_BTRUE, SIMP_SPECIAL_EXISTS_BFALSE. |
||
| Line 139: | Line 139: | ||
{{RRRow}}|*||{{Rulename|SIMP_FINITE_NATURAL1}}||<math> \finite (\natn ) \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FINITE_NATURAL1}}||<math> \finite (\natn ) \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FINITE_INTEGER}}||<math> \finite (\intg ) \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FINITE_INTEGER}}||<math> \finite (\intg ) \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_FINITE_BOOL}}||<math> \finite (\Bool ) \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FINITE_BOOL}}||<math> \finite (\Bool ) \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FINITE_LAMBDA}}||<math> \finite(\{x\qdot P\mid E\mapsto F\}) \;\;\defi\;\; \finite(\{x\qdot P\mid E\} ) </math>|| where <math>E</math> is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e., <math>E</math> is syntactically injective) and all identifiers bound by the comprehension set that occur in <math>F</math> also occur in <math>E</math> || A | {{RRRow}}|*||{{Rulename|SIMP_FINITE_LAMBDA}}||<math> \finite(\{x\qdot P\mid E\mapsto F\}) \;\;\defi\;\; \finite(\{x\qdot P\mid E\} ) </math>|| where <math>E</math> is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e., <math>E</math> is syntactically injective) and all identifiers bound by the comprehension set that occur in <math>F</math> also occur in <math>E</math> || A | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_EQUAL_EMPTY}}||<math> \mathit{Ty} = \emptyset \;\;\defi\;\; \bfalse </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_EQUAL_EMPTY}}||<math> \mathit{Ty} = \emptyset \;\;\defi\;\; \bfalse </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_IN}}||<math> t \in \mathit{Ty} \;\;\defi\;\; \btrue </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_IN}}||<math> t \in \mathit{Ty} \;\;\defi\;\; \btrue </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQV_BTRUE}}||<math> P \leqv \btrue \;\;\defi\;\; P </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQV_BTRUE}}||<math> P \leqv \btrue \;\;\defi\;\; P </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQV_BFALSE}}||<math> P \leqv \bfalse \;\;\defi\;\; \lnot\, P </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQV_BFALSE}}||<math> P \leqv \bfalse \;\;\defi\;\; \lnot\, P </math>|| || A | ||
Revision as of 09:08, 18 January 2011
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_AND_BTRUE |
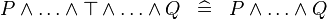 |
A | |
| * | SIMP_SPECIAL_AND_BFALSE |
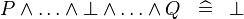 |
A | |
| * | SIMP_MULTI_AND |
 |
A | |
| * | SIMP_MULTI_AND_NOT |
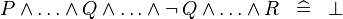 |
A | |
| * | SIMP_SPECIAL_OR_BTRUE |
 |
A | |
| * | SIMP_SPECIAL_OR_BFALSE |
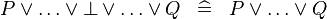 |
A | |
| * | SIMP_MULTI_OR |
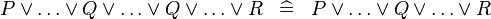 |
A | |
| * | SIMP_MULTI_OR_NOT |
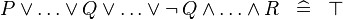 |
A | |
| * | SIMP_SPECIAL_IMP_BTRUE_R |
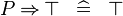 |
A | |
| * | SIMP_SPECIAL_IMP_BTRUE_L |
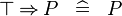 |
A | |
| * | SIMP_SPECIAL_IMP_BFALSE_R |
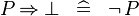 |
A | |
| * | SIMP_SPECIAL_IMP_BFALSE_L |
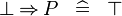 |
A | |
| * | SIMP_MULTI_IMP |
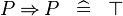 |
A | |
| * | SIMP_MULTI_IMP_OR |
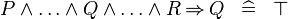 |
A | |
| * | SIMP_MULTI_IMP_AND_NOT_R |
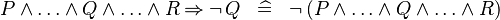 |
A | |
| * | SIMP_MULTI_IMP_AND_NOT_L |
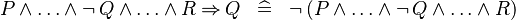 |
A | |
| * | SIMP_MULTI_EQV |
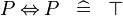 |
A | |
| * | SIMP_MULTI_EQV_NOT |
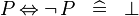 |
A | |
| * | SIMP_SPECIAL_NOT_BTRUE |
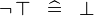 |
A | |
| * | SIMP_SPECIAL_NOT_BFALSE |
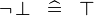 |
A | |
| * | SIMP_NOT_NOT |
 |
A | |
| * | SIMP_NOTEQUAL |
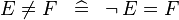 |
A | |
| * | SIMP_NOTIN |
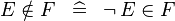 |
A | |
| * | SIMP_NOTSUBSET |
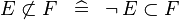 |
A | |
| * | SIMP_NOTSUBSETEQ |
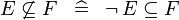 |
A | |
| * | SIMP_NOT_LE |
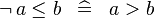 |
A | |
| * | SIMP_NOT_GE |
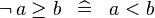 |
A | |
| * | SIMP_NOT_LT |
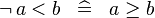 |
A | |
| * | SIMP_NOT_GT |
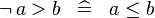 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_FALSE_R |
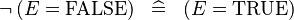 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_FALSE_L |
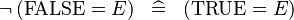 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_TRUE_R |
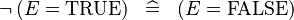 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_TRUE_L |
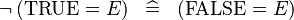 |
A | |
| * | SIMP_FORALL_AND |
 |
A | |
| * | SIMP_EXISTS_OR |
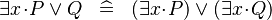 |
A | |
| * | SIMP_FORALL |
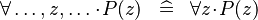 |
Quantified identifiers other than 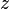 do not occur in do not occur in 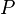 |
A |
| * | SIMP_EXISTS |
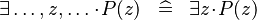 |
Quantified identifiers other than 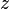 do not occur in do not occur in 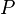 |
A |
| * | SIMP_MULTI_EQUAL |
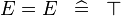 |
A | |
| * | SIMP_MULTI_NOTEQUAL |
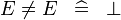 |
A | |
| * | SIMP_EQUAL_MAPSTO |
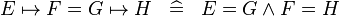 |
A | |
| * | SIMP_EQUAL_SING |
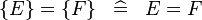 |
A | |
| * | SIMP_SPECIAL_EQUAL_TRUE |
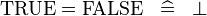 |
A | |
| * | SIMP_TYPE_SUBSETEQ |
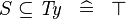 |
where  is a type expression is a type expression |
A |
| * | SIMP_SUBSETEQ_SING |
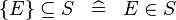 |
where  is a single expression is a single expression |
A |
| * | SIMP_SPECIAL_SUBSETEQ |
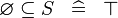 |
A | |
| * | SIMP_MULTI_SUBSETEQ |
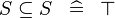 |
A | |
| * | SIMP_SUBSETEQ_BUNION |
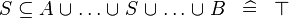 |
A | |
| * | SIMP_SUBSETEQ_BINTER |
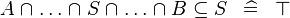 |
A | |
| * | DERIV_SUBSETEQ_BUNION |
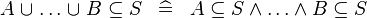 |
M | |
| * | DERIV_SUBSETEQ_BINTER |
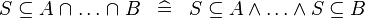 |
M | |
| * | SIMP_SPECIAL_IN |
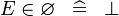 |
A | |
| * | SIMP_MULTI_IN |
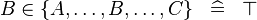 |
A | |
| * | SIMP_IN_SING |
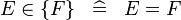 |
A | |
| * | SIMP_MULTI_SETENUM |
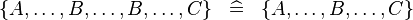 |
A | |
| * | SIMP_SPECIAL_BINTER |
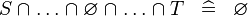 |
A | |
| * | SIMP_TYPE_BINTER |
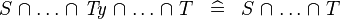 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_BINTER |
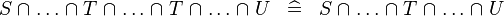 |
A | |
| * | SIMP_MULTI_EQUAL_BINTER |
 |
A | |
| * | SIMP_SPECIAL_BUNION |
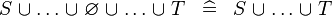 |
A | |
| * | SIMP_TYPE_BUNION |
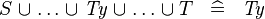 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_BUNION |
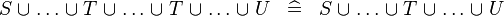 |
A | |
| * | SIMP_MULTI_EQUAL_BUNION |
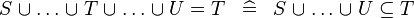 |
A | |
| * | SIMP_MULTI_SETMINUS |
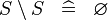 |
A | |
| * | SIMP_SPECIAL_SETMINUS_R |
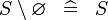 |
A | |
| * | SIMP_SPECIAL_SETMINUS_L |
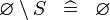 |
A | |
| * | SIMP_TYPE_SETMINUS |
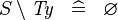 |
where  is a type expression is a type expression |
A |
| * | SIMP_TYPE_SETMINUS_SETMINUS |
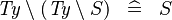 |
where  is a type expression is a type expression |
A |
| * | SIMP_KUNION_POW |
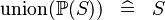 |
A | |
| * | SIMP_KUNION_POW1 |
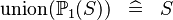 |
A | |
| * | SIMP_SPECIAL_KUNION |
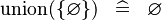 |
A | |
| * | SIMP_SPECIAL_QUNION |
 |
A | |
| * | SIMP_SPECIAL_KINTER |
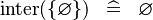 |
A | |
| * | SIMP_KINTER_POW |
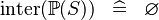 |
A | |
| * | SIMP_SPECIAL_POW |
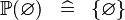 |
A | |
| * | SIMP_SPECIAL_POW1 |
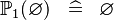 |
A | |
| * | SIMP_SPECIAL_CPROD_R |
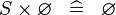 |
A | |
| * | SIMP_SPECIAL_CPROD_L |
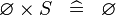 |
A | |
SIMP_COMPSET_EQUAL |
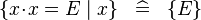 |
where  non free in non free in  |
A | |
| * | SIMP_COMPSET_IN |
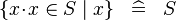 |
where  non free in non free in  |
A |
| * | SIMP_COMPSET_SUBSETEQ |
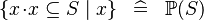 |
where  non free in non free in  |
A |
| * | SIMP_SPECIAL_COMPSET_BFALSE |
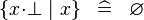 |
A | |
| * | SIMP_SPECIAL_COMPSET_BTRUE |
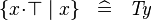 |
where the type of  is is  |
A |
| * | SIMP_SUBSETEQ_COMPSET_L |
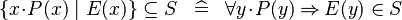 |
where 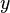 is fresh is fresh |
A |
| * | SIMP_SPECIAL_EQUAL_COMPSET |
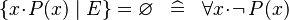 |
A | |
| * | SIMP_IN_COMPSET |
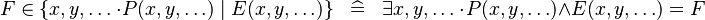 |
where  , , 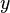 , , 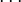 are not free in are not free in 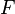 |
A |
| * | SIMP_IN_COMPSET_ONEPOINT |
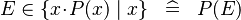 |
Equivalent to general simplification followed by One Point Rule application with the last conjunct predicate | A |
SIMP_SUBSETEQ_COMPSET_R |
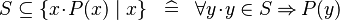 |
where 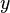 non free in non free in 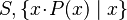 |
A | |
| * | SIMP_SPECIAL_OVERL |
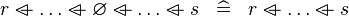 |
A | |
| * | SIMP_SPECIAL_KBOOL_BTRUE |
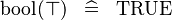 |
A | |
| * | SIMP_SPECIAL_KBOOL_BFALSE |
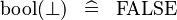 |
A | |
DISTRI_SUBSETEQ_BUNION_SING |
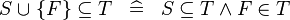 |
where 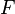 is a single expression is a single expression |
M | |
DEF_FINITE |
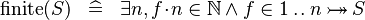 |
M | ||
| * | SIMP_SPECIAL_FINITE |
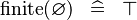 |
A | |
| * | SIMP_FINITE_SETENUM |
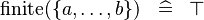 |
A | |
| * | SIMP_FINITE_BUNION |
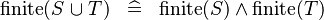 |
A | |
SIMP_FINITE_UNION |
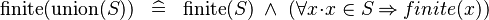 |
M | ||
SIMP_FINITE_QUNION |
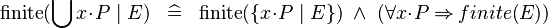 |
M | ||
| * | SIMP_FINITE_POW |
 |
A | |
| * | DERIV_FINITE_CPROD |
 |
A | |
| * | SIMP_FINITE_CONVERSE |
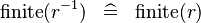 |
A | |
| * | SIMP_FINITE_UPTO |
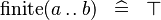 |
A | |
| * | SIMP_FINITE_ID |
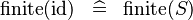 |
where 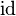 has type has type 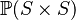 |
A |
| * | SIMP_FINITE_ID_DOMRES |
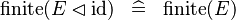 |
A | |
| * | SIMP_FINITE_PRJ1 |
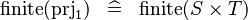 |
where 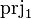 has type has type 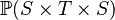 |
A |
| * | SIMP_FINITE_PRJ2 |
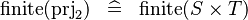 |
where 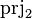 has type has type 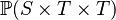 |
A |
| * | SIMP_FINITE_PRJ1_DOMRES |
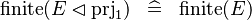 |
A | |
| * | SIMP_FINITE_PRJ2_DOMRES |
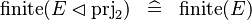 |
A | |
| * | SIMP_FINITE_NATURAL |
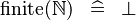 |
A | |
| * | SIMP_FINITE_NATURAL1 |
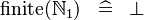 |
A | |
| * | SIMP_FINITE_INTEGER |
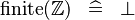 |
A | |
| * | SIMP_FINITE_BOOL |
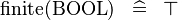 |
A | |
| * | SIMP_FINITE_LAMBDA |
 |
where  is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e., is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e.,  is syntactically injective) and all identifiers bound by the comprehension set that occur in is syntactically injective) and all identifiers bound by the comprehension set that occur in 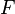 also occur in also occur in  |
A |
| * | SIMP_TYPE_EQUAL_EMPTY |
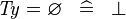 |
where  is a type expression is a type expression |
A |
| * | SIMP_TYPE_IN |
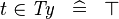 |
where  is a type expression is a type expression |
A |
| * | SIMP_SPECIAL_EQV_BTRUE |
 |
A | |
| * | SIMP_SPECIAL_EQV_BFALSE |
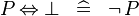 |
A | |
| * | DEF_SUBSET |
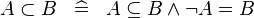 |
A | |
| * | SIMP_SPECIAL_SUBSET_R |
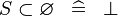 |
A | |
| * | SIMP_SPECIAL_SUBSET_L |
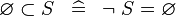 |
A | |
| * | SIMP_TYPE_SUBSET_L |
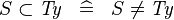 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_SUBSET |
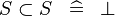 |
A | |
| * | SIMP_EQUAL_CONSTR |
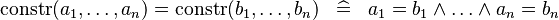 |
where 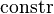 is a datatype constructor is a datatype constructor |
A |
| * | SIMP_EQUAL_CONSTR_DIFF |
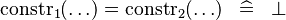 |
where 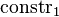 and and 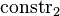 are different datatype constructors are different datatype constructors |
A |
| * | SIMP_DESTR_CONSTR |
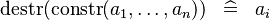 |
where 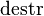 is the datatype destructor for the i-th argument of datatype constructor is the datatype destructor for the i-th argument of datatype constructor 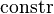 |
A |
| * | DISTRI_AND_OR |
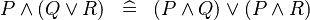 |
M | |
| * | DISTRI_OR_AND |
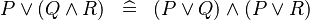 |
M | |
| * | DEF_OR |
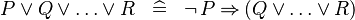 |
M | |
| * | DERIV_IMP |
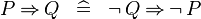 |
M | |
| * | DERIV_IMP_IMP |
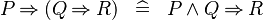 |
M | |
| * | DISTRI_IMP_AND |
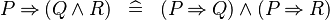 |
M | |
| * | DISTRI_IMP_OR |
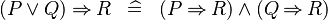 |
M | |
| * | DEF_EQV |
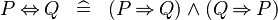 |
M | |
| * | DISTRI_NOT_AND |
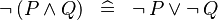 |
M | |
| * | DISTRI_NOT_OR |
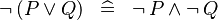 |
M | |
| * | DERIV_NOT_IMP |
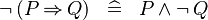 |
M | |
| * | DERIV_NOT_FORALL |
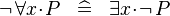 |
M | |
| * | DERIV_NOT_EXISTS |
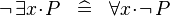 |
M | |
| * | DEF_SPECIAL_NOT_EQUAL |
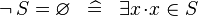 |
where  is not free in is not free in  |
M |
| * | DEF_IN_MAPSTO |
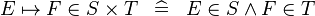 |
M | |
| * | DEF_IN_POW |
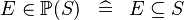 |
M | |
| * | DEF_IN_POW1 |
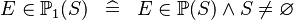 |
M | |
| * | DEF_SUBSETEQ |
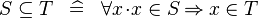 |
where  is not free in is not free in  or or  |
M |
| * | DEF_IN_BUNION |
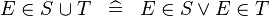 |
M | |
| * | DEF_IN_BINTER |
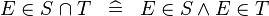 |
M | |
| * | DEF_IN_SETMINUS |
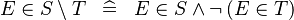 |
M | |
| * | DEF_IN_SETENUM |
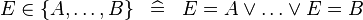 |
M | |
| * | DEF_IN_KUNION |
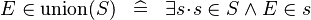 |
where  is fresh is fresh |
M |
| * | DEF_IN_QUNION |
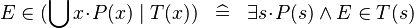 |
where  is fresh is fresh |
M |
| * | DEF_IN_KINTER |
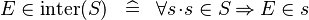 |
where  is fresh is fresh |
M |
| * | DEF_IN_QINTER |
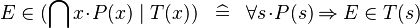 |
where  is fresh is fresh |
M |
| * | DEF_IN_UPTO |
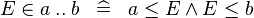 |
M | |
| * | DISTRI_BUNION_BINTER |
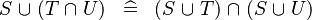 |
M | |
| * | DISTRI_BINTER_BUNION |
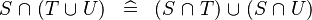 |
M | |
DISTRI_BINTER_SETMINUS |
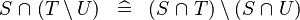 |
M | ||
DISTRI_SETMINUS_BUNION |
 |
M | ||
| * | DERIV_TYPE_SETMINUS_BINTER |
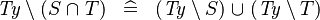 |
where  is a type expression is a type expression |
M |
| * | DERIV_TYPE_SETMINUS_BUNION |
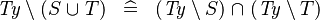 |
where  is a type expression is a type expression |
M |
| * | DERIV_TYPE_SETMINUS_SETMINUS |
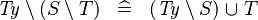 |
where  is a type expression is a type expression |
M |
DISTRI_CPROD_BINTER |
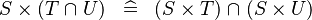 |
M | ||
DISTRI_CPROD_BUNION |
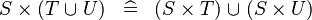 |
M | ||
DISTRI_CPROD_SETMINUS |
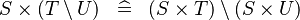 |
M | ||
| * | DERIV_SUBSETEQ |
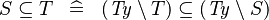 |
where 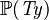 is the type of is the type of  and and  |
M |
| * | DERIV_EQUAL |
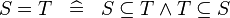 |
where 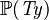 is the type of is the type of  and and  |
M |
| * | DERIV_SUBSETEQ_SETMINUS_L |
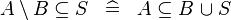 |
M | |
| * | DERIV_SUBSETEQ_SETMINUS_R |
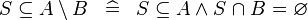 |
M | |
| * | DEF_PARTITION |
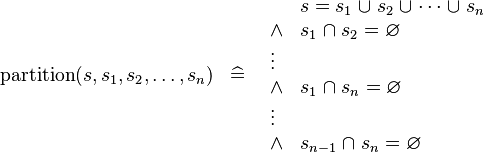 |
AM |