Structured Types: Difference between revisions

From Event-B
Jump to navigationJump to search
← Older editNewer edit →
imported>WikiSysop
imported>WikiSysop
Line 2: Line 2:


The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures.
The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures.
Nevertheless it is possible to model structured types using projection functions to represent the fields/ attributes.  For example,
Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes.  For example,
suppose we wish to model a structured type C with fields e and f (with type E and F respectively).
suppose we wish to model a record structure 'C' with fields 'e' and 'f' (with type E and F respectively).
Let us use the following syntax for this (not part of Event-B):
Let us use the following syntax for this (not part of Event-B):


Line 9: Line 9:
{{SimpleHeader}}
{{SimpleHeader}}
|<math> \begin{array}{lcl}
|<math> \begin{array}{lcl}
  \textbf{STRUCT}~~~~ C &::&  e\in E\\
  \textbf{RECORD}~~~~ C &::&  e\in E\\
     &&  f \in F
     &&  f \in F
  \end{array}  
  \end{array}  
Line 35: Line 35:




'''Names in the proof tree:''' Predicate Prover
Now, given an element <math>c\in C</math> representing a record, we write <math>e(c)</math> for the 'e' component of structure
 
'''Names in the preferences:''' PP restricted, PP after lasso, PP unrestricted
 
'''Input:''' In the configuration "restricted" all selected hypotheses and the goal are passed to New PP.
In the configuration "after lasso" a lasso operation is applied to the selected hypotheses and the goal and the result is passed to New PP.
The lasso operation selects any unselected hypothesis that has a common symbol with the goal or a hypothesis that was selected before.
In the configuration "unrestricted" all the available hypotheses are passed to New PP.
 
'''How the Prover Proceeds:''' First, all function and predicate symbols that are different from "<math>\in</math>" and not related to arithmetic are translated away. For example <math>A \subseteq B</math> is translated to <math>\forall x\cdot x \in A \limp x \in B</math>. Then New PP translates the proof obligation to CNF (conjunctive normal form) and applies a combination of unit resolution and the Davis Putnam algorithm.
 
'''Some Strengths:'''
* New PP outputs a set of "used hypotheses". If an unused hypotheses changes, the old proof can be reused.
* New PP has limited support for equational reasoning.

Revision as of 16:03, 1 May 2009

Modelling Structured Types

The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes. For example, suppose we wish to model a record structure 'C' with fields 'e' and 'f' (with type E and F respectively). Let us use the following syntax for this (not part of Event-B):

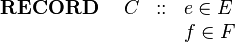
\begin{array}{lcl} \textbf{RECORD}~~~~ C &::& e\in E\\ && f \in F \end{array}

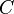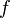We can model this structure in Event-B by introducing (in a context) a set C and two functions e and f as constants as follows:

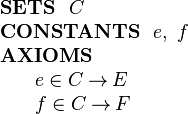
\begin{array}{l} \textbf{SETS}~~ C\\ \textbf{CONSTANTS}~~ e,~ f\\ \textbf{AXIOMS}\\ ~~~~\begin{array}{l} e \in C \tfun E\\ f \in C \tfun F\\ \end{array} \end{array}


Now, given an element 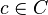c\in C representing a record, we write 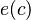e(c) for the 'e' component of structure

Retrieved from ‘https://wiki.event-b.org/index.php?title=Structured_Types&oldid=9538’