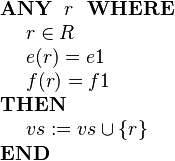Structured Types: Difference between revisions
imported>WikiSysop |
imported>WikiSysop No edit summary |
||
| Line 3: | Line 3: | ||
The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. | The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. | ||
Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes. For example, | Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes. For example, | ||
suppose we wish to model a record structure '' | suppose we wish to model a record structure ''R'' with fields ''e'' and ''f'' (with type ''E'' and ''F'' respectively). | ||
Let us use the following syntax for this (not part of Event-B syntax): | Let us use the following syntax for this (not part of Event-B syntax): | ||
| Line 9: | Line 9: | ||
{{SimpleHeader}} | {{SimpleHeader}} | ||
|<math> \begin{array}{lcl} | |<math> \begin{array}{lcl} | ||
\textbf{RECORD}~~~~ | \textbf{RECORD}~~~~ R &::& e\in E\\ | ||
&& f \in F | && f \in F | ||
\end{array} | \end{array} | ||
| Line 16: | Line 16: | ||
</center> | </center> | ||
We can model this structure in Event-B by introducing (in a context) a carrier set '' | We can model this structure in Event-B by introducing (in a context) a carrier set ''R'' and two | ||
functions ''e'' and ''f'' as constants as follows: | functions ''e'' and ''f'' as constants as follows: | ||
| Line 22: | Line 22: | ||
{{SimpleHeader}} | {{SimpleHeader}} | ||
|<math> \begin{array}{l} | |<math> \begin{array}{l} | ||
\textbf{SETS}~~ | \textbf{SETS}~~ R\\ | ||
\textbf{CONSTANTS}~~ e,~ f\\ | \textbf{CONSTANTS}~~ e,~ f\\ | ||
\textbf{AXIOMS}\\ | \textbf{AXIOMS}\\ | ||
~~~~\begin{array}{l} | ~~~~\begin{array}{l} | ||
e \in | e \in R \tfun E\\ | ||
f \in | f \in R \tfun F\\ | ||
\end{array} | \end{array} | ||
\end{array} | \end{array} | ||
| Line 35: | Line 35: | ||
Now, given an element <math> | Now, given an element <math>r\in R</math> representing a record structure, we write <math>e(r)</math> for the ''e'' component of ''r'' and <math>f(r)</math> for the ''f'' component of ''r''. | ||
''E'' and ''F'' can be any type definable in Event-B, including a type representing a record structure. | ''E'' and ''F'' can be any type definable in Event-B, including a type representing a record structure. | ||
| Line 41: | Line 41: | ||
==Constructing Structured Values== | ==Constructing Structured Values== | ||
Suppose we have a variable ''v'' in a machine whose type is the structure '' | Suppose we have a variable ''v'' in a machine whose type is the structure ''R'' defined above: | ||
<center> | <center> | ||
<math>\ | <math>\textbf{VARIABLE}~~ v\in R</math> | ||
</center> | </center> | ||
We wish to assign a structured value to ''v'' whose ''e'' field has some value ''e1'' and whose ''f'' field has some value ''f1''. | We wish to assign a structured value to ''v'' whose ''e'' field has some value ''e1'' and whose ''f'' field has some value ''f1''. | ||
This can be achieved by specifying the choice of an event parameter '' | This can be achieved by specifying the choice of an event parameter ''r'' whose fields are constrained by appropriate guards | ||
and assigning parameter '' | and assigning parameter ''r'' to the machine variable ''v''. This is shown in the following event: | ||
<center><math> | <center><math> | ||
\begin{array}{l} | \begin{array}{l} | ||
\ | \textbf{ANY}~~ r ~~\textbf{WHERE} \\ | ||
~~~~ | ~~~~ r \in R \\ | ||
~~~~ e( | ~~~~ e( r ) = e1 \\ | ||
~~~~ f( | ~~~~ f( r ) = f1 \\ | ||
\ | \textbf{THEN} \\ | ||
~~~~ v := | ~~~~ v := r \\ | ||
\ | \textbf{END} | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
| Line 66: | Line 66: | ||
<center><math> | <center><math> | ||
\begin{array}{l} | \begin{array}{l} | ||
\ | \textbf{ANY}~~ r ~~\textbf{WHERE} \\ | ||
~~~~ | ~~~~ r \in R \\ | ||
~~~~ e( | ~~~~ e( r ) = e1 \\ | ||
~~~~ f( | ~~~~ f( r ) = f(v) \\ | ||
\ | \textbf{THEN} \\ | ||
~~~~ v := | ~~~~ v := r \\ | ||
\ | \textbf{END} | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
| Line 80: | Line 80: | ||
<center><math> | <center><math> | ||
\begin{array}{l} | \begin{array}{l} | ||
\ | \textbf{ANY}~~ r ~~\textbf{WHERE} \\ | ||
~~~~ | ~~~~ r \in R \\ | ||
~~~~ e( | ~~~~ e( r ) = e1 \\ | ||
\ | \textbf{THEN} \\ | ||
~~~~ v := | ~~~~ v := r \\ | ||
\ | \textbf{END} | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
| Line 92: | Line 92: | ||
Sometimes we will wish to model a set of structured elements as a machine variable, e.g., | Sometimes we will wish to model a set of structured elements as a machine variable, e.g., | ||
<center> | <center> | ||
<math>\ | <math>\textbf{VARIABLE}~~ vs\subseteq R</math> | ||
</center> | </center> | ||
| Line 98: | Line 98: | ||
<center><math> | <center><math> | ||
\begin{array}{l} | \begin{array}{l} | ||
\ | \textbf{ANY}~~ r ~~\textbf{WHERE} \\ | ||
~~~~ | ~~~~ r \in R \\ | ||
~~~~ e( | ~~~~ e( r ) = e1 \\ | ||
~~~~ f( | ~~~~ f( r ) = f1 \\ | ||
\ | \textbf{THEN} \\ | ||
~~~~ vs := vs \cup \{ | ~~~~ vs := vs \cup \{r\} \\ | ||
\ | \textbf{END} | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
Revision as of 16:03, 5 May 2009
Modelling Structured Types
The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes. For example, suppose we wish to model a record structure R with fields e and f (with type E and F respectively). Let us use the following syntax for this (not part of Event-B syntax):
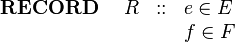
|
We can model this structure in Event-B by introducing (in a context) a carrier set R and two functions e and f as constants as follows:
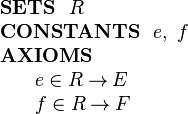
|
Now, given an element 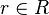 representing a record structure, we write
representing a record structure, we write 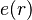 for the e component of r and
for the e component of r and 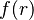 for the f component of r.
for the f component of r.
E and F can be any type definable in Event-B, including a type representing a record structure.
Constructing Structured Values
Suppose we have a variable v in a machine whose type is the structure R defined above:
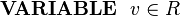
We wish to assign a structured value to v whose e field has some value e1 and whose f field has some value f1. This can be achieved by specifying the choice of an event parameter r whose fields are constrained by appropriate guards and assigning parameter r to the machine variable v. This is shown in the following event:
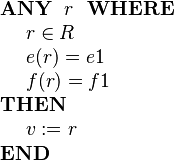
If we only wish to update some fields and leave others changed, this needs to be done by specifying explicitly that some fields remain unchanged. This is shown in the following example where only the e field is modified:
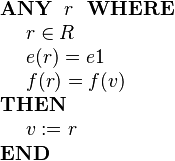
If we don't care about the value of some field (e.g., f), we simply omit any guard on that field as follows:
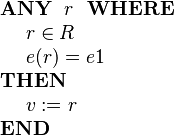
Sometimes we will wish to model a set of structured elements as a machine variable, e.g.,
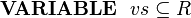
We can add a structured element to this set using the following event: