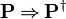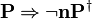Variations in HYP, CNTR and GenMP: Difference between revisions
imported>Josselin created page |
imported>Josselin Explain the context, the objective and the conventions |
||
| Line 1: | Line 1: | ||
This page explains how the variants array in [[Inference Rules]] have been generated. | This page explains how the variants array in [[Inference Rules]] have been generated. | ||
= Context = | |||
The reasoners implementing the inference rules HYP, HYP_OR, CNTR and | The reasoners implementing the inference rules HYP, HYP_OR, CNTR and GENMP_* look for exact matches of a predicate. But, quite often a relational predicate no exact matches (for instance, because it has been normalized). Moreover, there is sometimes a variant which is equivalent to the predicate which is checked. For instance, "¬ a = b" is equivalent to "¬ b = a". Finally, the reasoners shall also consider variants which are a sufficient condition for the rule. For instance, if the goal is "a ≤ b", then a hypothesis "a < b" is a sufficient condition to discharge the goal with HYP. | ||
= Objective = | |||
The reasoners implementing these inference rules should take into account such variants of <math>\textbf{P} </math> and <math> \lnot \textbf{P} </math> when looking for occurrences. | |||
= Conventions = | |||
These variants have been generated based on the following | |||
rules: | |||
* <math> \textbf{P} \limp \textbf{P}^{\dagger} </math> | |||
* <math> \textbf{P} \limp \lnot \textbf{nP}^{\dagger} </math> | |||
In the case of the predicate which is checked is positive the default value of <math> \textbf{P}^{\dagger} </math> is <math> \textbf{P} </math> and this of <math> \textbf{nP}^{\dagger} </math> is <math> \lnot \textbf{P} </math>. If the predicate is negative, the default value of <math> \textbf{nP}^{\dagger} </math> is <math> \textbf{P} </math>. However, the negative arithmetic predicates are not taken into account by the reasoners implementing those inference rules because these reasonner are applied after such normalization of relational predicates. For instance, "¬ a < b" is normalized to "b ≤ a". There is an exception in the case "¬ a = b", this predicate is allowed by the normalization. | |||
Revision as of 09:23, 1 August 2013
This page explains how the variants array in Inference Rules have been generated.
Context
The reasoners implementing the inference rules HYP, HYP_OR, CNTR and GENMP_* look for exact matches of a predicate. But, quite often a relational predicate no exact matches (for instance, because it has been normalized). Moreover, there is sometimes a variant which is equivalent to the predicate which is checked. For instance, "¬ a = b" is equivalent to "¬ b = a". Finally, the reasoners shall also consider variants which are a sufficient condition for the rule. For instance, if the goal is "a ≤ b", then a hypothesis "a < b" is a sufficient condition to discharge the goal with HYP.
Objective
The reasoners implementing these inference rules should take into account such variants of 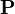 and
and 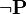 when looking for occurrences.
when looking for occurrences.
Conventions
These variants have been generated based on the following rules:
In the case of the predicate which is checked is positive the default value of 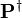 is
is 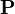 and this of
and this of 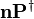 is
is 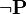 . If the predicate is negative, the default value of
. If the predicate is negative, the default value of 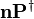 is
is 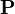 . However, the negative arithmetic predicates are not taken into account by the reasoners implementing those inference rules because these reasonner are applied after such normalization of relational predicates. For instance, "¬ a < b" is normalized to "b ≤ a". There is an exception in the case "¬ a = b", this predicate is allowed by the normalization.
. However, the negative arithmetic predicates are not taken into account by the reasoners implementing those inference rules because these reasonner are applied after such normalization of relational predicates. For instance, "¬ a < b" is normalized to "b ≤ a". There is an exception in the case "¬ a = b", this predicate is allowed by the normalization.