Event-B Qualitative Probability User Guide: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Son |
imported>Son |
||
| Line 57: | Line 57: | ||
[[Image:contention-po.jpg]] | [[Image:contention-po.jpg]] | ||
* The goal of proof obligation '''resolve/PRV''' is <math>\exists x^\prime, y^\prime \qdot \Bool \setminus \{x^\prime, y^\prime\} \subset \Bool \setminus \{x, y\}</math>. With hypothesis <math>x = y</math> (from the guard of the event), the proof obligation can be discharged by instantiating different values for <math>x^\prime</math> and <math>y^\prime</math> (e.g. <math>\True</math> for <math>x^\prime</math> and <math>\False</math> for <math>y^\prime</math>. Alternatively, the obligation can be interactively discharge using '''p1''' (AterlierB Predicate Prover on lasso'd hypotheses) directly as shown below | * The goal of proof obligation '''resolve/PRV''' is <math>\exists x^\prime, y^\prime \qdot \Bool \setminus \{x^\prime, y^\prime\} \subset \Bool \setminus \{x, y\}</math>. With hypothesis <math>x = y</math> (from the guard of the event), the proof obligation can be discharged by instantiating different values for <math>x^\prime</math> and <math>y^\prime</math> (e.g. <math>\True</math> for <math>x^\prime</math> and <math>\False</math> for <math>y^\prime</math>). Alternatively, the obligation can be interactively discharge using '''p1''' (AterlierB Predicate Prover on lasso'd hypotheses) directly as shown below | ||
[[Image:resolve-prv.jpg]] | [[Image:resolve-prv.jpg]] | ||
Revision as of 13:46, 23 November 2011
User:Son at ETH Zurich is in charge of the plug-in.
Introduction
Event-B Qualitative Probability plug-in provides supports for reasoning about termination with probability 1 (almost-certain termination).
Installing and Updating
The plug-in is available through the main Rodin Update Site under Modelling Extension category.
News
- 23.11.2011: Version 0.2.1 released for Rodin 2.3.*
Technical References
- S. Hallerstede, T.S. Hoang. Qualitative Probabilistic Modelling in Event-B. In IFM 2007: Integrated Formal Methods, 6th International Conference Proceedings, Oxford, UK, July 2-5, 2007, volume 4591 of LNCS © Springer-Verlag. Springer website
- Initial idea about probabilistic convergence event.
- New modelling elements: Variant bound
- New proof obligations: PRV, BND, FINACT.
- Example: Resolve contention in IEEE 1395 (Firewire protocol).
- E. Yilmaz, T.S. Hoang. Development of Rabin’s Choice Coordination Algorithm in Event-B. In Automated Verification of Critical Systems 2010, volume 35 of Electronic Communications of the EASST © EASST. EASST website
- Probablistic convergence event with refinement
- Constraints on how (not-) to refine probabilistic events.
- Example: Rabin's Choice Coordination Algorithm.
Usage
We illustrate the usage of the plug-in using the example of contention resolving (part of IEEE 1394 Firewire protocol).
Description
Two processes in contention use a probabilistic protocol to resolve the problem. In each step, each process probabilisitcally choose to communicate in either short or long delay. The contention is resolved when the processes choose different delays.
Nondetermistic specification
- Boolean variables
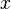 and
and 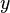 represent the choice for each process:
represent the choice for each process: 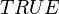 for short delay
for short delay 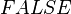 for long delay.
for long delay.
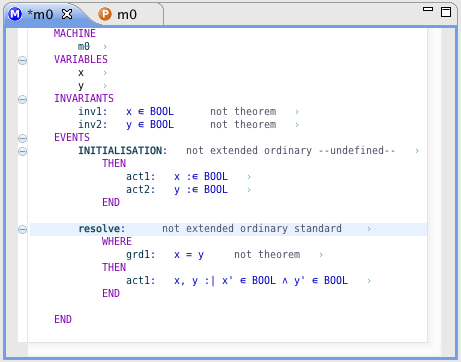
- Resolving contention is model as an event of the model with guard
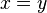 (i.e. keep trying when the choices are identical).
(i.e. keep trying when the choices are identical).
Probabilistic specification
- To set event resolve is probabilistic convergence:
- Go to the Edit page of the standard Rodin Editor.
- Open the EVENTS section
- Set convergence attribute of resolve from ordinary to convergent.
- Set probabilistic attribute of resolve from standard to probabilistic.
- Set
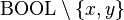 as the variant of the model
as the variant of the model
- Set
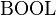 as the bound of the model
as the bound of the model
- Save the model
Proof Obligations
- The model should have 3 proof obligations including resolve/PRV.
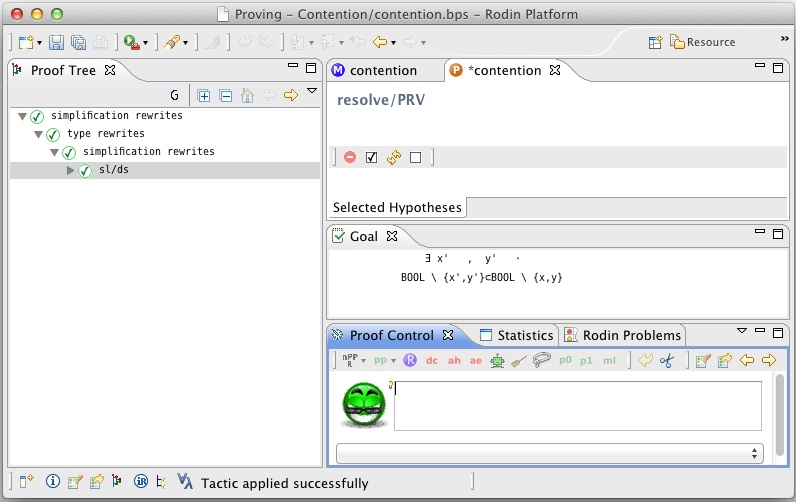
- The goal of proof obligation resolve/PRV is
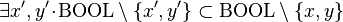 . With hypothesis
. With hypothesis 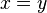 (from the guard of the event), the proof obligation can be discharged by instantiating different values for
(from the guard of the event), the proof obligation can be discharged by instantiating different values for 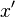 and
and 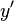 (e.g.
(e.g. 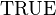 for
for 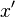 and
and 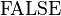 for
for 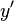 ). Alternatively, the obligation can be interactively discharge using p1 (AterlierB Predicate Prover on lasso'd hypotheses) directly as shown below
). Alternatively, the obligation can be interactively discharge using p1 (AterlierB Predicate Prover on lasso'd hypotheses) directly as shown below