Generic Instantiation: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Son |
imported>Son |
||
| Line 7: | Line 7: | ||
<math> | <math> | ||
S \neq \emptyset | S \neq \emptyset | ||
</math> | </math> | ||
<math>\forall x \qdot x \in S</math> | <math>\forall x \qdot x \in S</math> | ||
Both these axioms can be generated as theorems in the instantiating context which need to be proved. | |||
However, the second theorem can be proved if <code>S</code> is instantiated to another carrier set in the instantiating context. | |||
This could be a limitation of generic instantiation (<font color=red>to be discussed</font>) | |||
Revision as of 16:17, 26 March 2010
The initial proposal from Southampton is as follows. File:Proposal generic instantiation rodin.pdf.
Issues: Instantiation of Carrier Sets
Currently, the proposal mentions that the carrier sets can be instantiated to any set expressions (which contains existing carrier sets and constants). Beside the declared axioms in the development to be extended there are two hidden axioms about a carrier set S
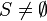
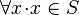
Both these axioms can be generated as theorems in the instantiating context which need to be proved.
However, the second theorem can be proved if S is instantiated to another carrier set in the instantiating context.
This could be a limitation of generic instantiation (to be discussed)