How Rodin Deviates from Abrial's Book: Difference between revisions
imported>Ladenberger |
imported>Ladenberger |
||
| Line 11: | Line 11: | ||
On the one hand, the proof calculus devised in Chapter 9 allows one to prove <math>1\div 0 = 1\div0</math>. | On the one hand, the proof calculus devised in Chapter 9 allows one to prove <math>1\div 0 = 1\div0</math>. | ||
On the other hand, it is impossible to prove <math>1\div0=1\div0</math> in Rodin, because <math>1\div0</math> is regarded as ill-defined. | On the other hand, it is impossible to prove <math>1\div0=1\div0</math> in Rodin, because <math>1\div0</math> is regarded as ill-defined. | ||
Well-definedness is described [http://handbook.event-b.org/current/html/well_definedness.html | Well-definedness is described [http://handbook.event-b.org/current/html/well_definedness.html here] and [[Event-B Mathematical Language|here]]. | ||
=== Proof Calculus === | === Proof Calculus === | ||
The proof calculus used in Abrial's book is different from the proof calculus implemented by Rodin, i.e., rules have different names, and some rules available in Abrial's book are unavailable in Rodin and vice versa. | The proof calculus used in Abrial's book is different from the proof calculus implemented by Rodin, i.e., rules have different names, and some rules available in Abrial's book are unavailable in Rodin and vice versa. | ||
Revision as of 10:42, 27 October 2011
This page summarizes (some) differences between the version of Event-B described in Abrial's book an the version implemented by Rodin.
Types
One may understand from Chapter 9 that Event-B is based on naive set theory, and therefore has terms like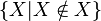 
.
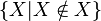This is not the case in Rodin: in Rodin terms are typed similarly as in higher order logic, and is therefore ill-typed.
For the details see the page about the Event-B Mathematical Language.
Well-Definedness
On the one hand, the proof calculus devised in Chapter 9 allows one to prov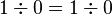e 
.
On the other hand, it is impossible to prove 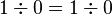in Rodin, because 
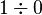is regarded as ill-defined.
Well-definedness is described here and here.
Proof Calculus
The proof calculus used in Abrial's book is different from the proof calculus implemented by Rodin, i.e., rules have different names, and some rules available in Abrial's book are unavailable in Rodin and vice versa.
