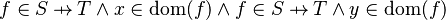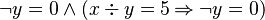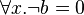Improved WD Lemma Generation: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Desaperh mNo edit summary |
imported>Desaperh mNo edit summary |
||
| Line 16: | Line 16: | ||
The well-definedness lemma generated for predicate <math> \exists x.x=a\div b </math> is | The well-definedness lemma generated for predicate <math> \exists x.x=a\div b </math> is | ||
<math> \forall x.\lnot b </math> | <math> \forall x.\lnot b=0 </math> | ||
This predicate is sub-optimal as <math> \forall x </math> is unneccesary. | This predicate is sub-optimal as <math> \forall x </math> is unneccesary. | ||
[[Category:Developer documentation]] | [[Category:Developer documentation]] | ||
Revision as of 14:58, 21 April 2010
This page describes work in progress for optimising well-definedness lemmas generated by the Core Rodin platform.
Motivating examples
With Rodin 1.3, the well-definedness lemma generated for predicate 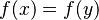 is
is
This predicate is sub-optimal as it contains twice the same sub-predicate (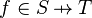 ). Consequently, when the prover is fed with the generated lemma, it will have to prove twice the same goal.
). Consequently, when the prover is fed with the generated lemma, it will have to prove twice the same goal.
The well-definedness lemma generated for predicate 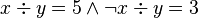 is
is
This predicate is sub-optimal as the sub-predicate 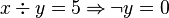 is subsumed by the sub-predicate
is subsumed by the sub-predicate 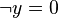 . The prover doesn't need to prove
. The prover doesn't need to prove 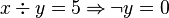 if
if 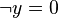 has been proved.
has been proved.
The well-definedness lemma generated for predicate 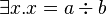 is
is
This predicate is sub-optimal as 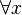 is unneccesary.
is unneccesary.