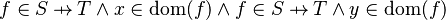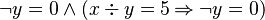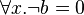Improved WD Lemma Generation

This page describes work in progress for optimising well-definedness lemmas generated by the Core Rodin platform.

The lemmas are generated according to the 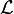$\mathcal{L}$ operator defined in Well-definedness in Event-B. However, this operator being defined as a syntactic transformation, it sometimes generates lemmas that are unnecessarily complicated. We first give some motivating examples showing cases where this happens, then we describe what result shall be produced by the tool. Finally, we describe the design retained for development.

Motivating examples

With Rodin 1.3, the well-definedness lemma generated for predicate 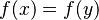$f(x) = f(y)$ is

$f\in S\pfun T\land x\in\dom(f)\land f\in S\pfun T\land y\in\dom(f)$

This predicate is sub-optimal as it contains twice the same sub-predicate (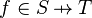$f\in S\pfun T$). Consequently, when the prover is fed with the generated lemma, it will have to prove twice the same goal.

The well-definedness lemma generated for predicate 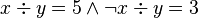$x \div y=5 \land \lnot x \div y=3$ is

$\lnot y=0 \land (x\div y=5 \limp \lnot y=0)$ 

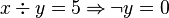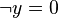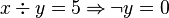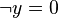This predicate is sub-optimal as the sub-predicate $x\div y=5 \limp \lnot y=0$ is subsumed by the sub-predicate $\lnot y=0$. The prover doesn't need to prove $x\div y=5 \limp \lnot y=0$ if $\lnot y=0$ has been proved.

The well-definedness lemma generated for predicate 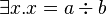$\exists x.x=a\div b$ is

$\forall x.\lnot b=0$

This predicate is sub-optimal as 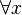$\forall x$ is unnecessary.

Improved Generation

To fix the issues shown in the above examples, we need that the tool produces a WD lemma equivalent (in the logical sense) to the predicate obtained through the 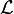$\mathcal{L}$ operator and satisfying the following constraints:

• No sub-predicate subsumes another sub-predicate

TODO: Is there any other constraint to add?

Design for Improved Generation

TODO: Do the design