Induction proof: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Christophe No edit summary |
imported>Christophe No edit summary |
||
| Line 17: | Line 17: | ||
<math> | <math> | ||
\forall s.s \subseteq \mathbb{N} \land 0 \in s \land (\forall n.n \in s => n+1 \in s)\Rightarrow N \subseteq s | \forall s.s \subseteq \mathbb{N} \land 0 \in s \land (\forall n.n \in s => n+1 \in s)\Rightarrow N \subseteq s | ||
</math> | |||
---- | |||
The proof of the previous theorem is given by the following. <br/> | |||
Instanciate the key theorem with : <math> \{x|x\in \mathbb{N} \land P(x)\}</math> | |||
Revision as of 21:22, 13 October 2008
This page explains how to proove with induction method on the natural number with Rodin tools.
In other words, how to proove :
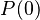
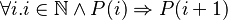
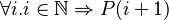
The proof key is the following theorem:
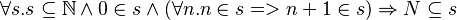
The proof of the previous theorem is given by the following.
Instanciate the key theorem with :