Inference Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Frederic New page: {{RRHeader}} {{RRRow}}|<font size="-2"> HYP </font>|| <math>\frac{}{\textbf{H},\textbf{P} \;\;\vdash \;\; \textbf{P}} </math>|| || A {{RRRow}}|<font size="-2"> HYP_OR </font>|| <math>\f... |
imported>Laurent Added star column |
||
| Line 1: | Line 1: | ||
Conventions used in these tables are described in [[The_Proving_Perspective_%28Rodin_User_Manual%29#Inference_rules]] | |||
{{RRHeader}} | {{RRHeader}} | ||
{{RRRow}}|<font size="-2"> HYP </font>|| <math>\frac{}{\textbf{H},\textbf{P} \;\;\vdash \;\; \textbf{P}} </math>|| || A | {{RRRow}}|*||<font size="-2"> HYP </font>|| <math>\frac{}{\textbf{H},\textbf{P} \;\;\vdash \;\; \textbf{P}} </math>|| || A | ||
{{RRRow}}|<font size="-2"> HYP_OR </font>|| <math>\frac{}{\textbf{H},\textbf{Q} \;\;\vdash \;\; \textbf{P} \lor \ldots \lor \textbf{Q} \lor \ldots \lor \textbf{R}}</math> || || A | {{RRRow}}|*||<font size="-2"> HYP_OR </font>|| <math>\frac{}{\textbf{H},\textbf{Q} \;\;\vdash \;\; \textbf{P} \lor \ldots \lor \textbf{Q} \lor \ldots \lor \textbf{R}}</math> || || A | ||
{{RRRow}}|<font size="-2"> CNTR </font>|| <math>\frac{}{\textbf{H},\;\textbf{P},\;\neg\,\textbf{P} \;\;\vdash \;\; \textbf{Q}}</math> || || A | {{RRRow}}|*||<font size="-2"> CNTR </font>|| <math>\frac{}{\textbf{H},\;\textbf{P},\;\neg\,\textbf{P} \;\;\vdash \;\; \textbf{Q}}</math> || || A | ||
{{RRRow}}|<font size="-2"> FALSE_HYP </font>|| <math>\frac{}{\textbf{H},\bfalse \;\;\vdash \;\; \textbf{P}}</math> || || A | {{RRRow}}|*||<font size="-2"> FALSE_HYP </font>|| <math>\frac{}{\textbf{H},\bfalse \;\;\vdash \;\; \textbf{P}}</math> || || A | ||
{{RRRow}}|<font size="-2"> TRUE_GOAL </font>|| <math>\frac{}{\textbf{H} \;\;\vdash \;\; \btrue}</math> || || A | {{RRRow}}|*||<font size="-2"> TRUE_GOAL </font>|| <math>\frac{}{\textbf{H} \;\;\vdash \;\; \btrue}</math> || || A | ||
{{RRRow}}|<font size="-2"> DBL_HYP </font>|| <math>\frac{\textbf{H},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}{\textbf{H},\;\textbf{P},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}</math> || || A | {{RRRow}}|*||<font size="-2"> DBL_HYP </font>|| <math>\frac{\textbf{H},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}{\textbf{H},\;\textbf{P},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}</math> || || A | ||
{{RRRow}}|<font size="-2"> AND_L </font>|| <math>\frac{\textbf{H},\textbf{P},\textbf{Q} \; \; \vdash \; \; \textbf{R}}{\textbf{H},\; \textbf{P} \land \textbf{Q} \; \; \vdash \; \; | {{RRRow}}|*||<font size="-2"> AND_L </font>|| <math>\frac{\textbf{H},\textbf{P},\textbf{Q} \; \; \vdash \; \; \textbf{R}}{\textbf{H},\; \textbf{P} \land \textbf{Q} \; \; \vdash \; \; | ||
\textbf{R}}</math> || || A | \textbf{R}}</math> || || A | ||
{{RRRow}}|<font size="-2"> AND_R </font>|| <math>\frac{\textbf{H} \; \; \vdash \; \; \textbf{P} \qquad \textbf{H} \; \; \vdash \; \; \textbf{Q}}{\textbf{H} \; \; \vdash \; \; \textbf{P} \; \land \; \textbf{Q}}</math> || || A | {{RRRow}}|*||<font size="-2"> AND_R </font>|| <math>\frac{\textbf{H} \; \; \vdash \; \; \textbf{P} \qquad \textbf{H} \; \; \vdash \; \; \textbf{Q}}{\textbf{H} \; \; \vdash \; \; \textbf{P} \; \land \; \textbf{Q}}</math> || || A | ||
{{RRRow}}|<font size="-2"> IMP_L1 </font>|| <math>\frac{\textbf{H},\; \textbf{Q},\; \textbf{P} \land \ldots \land \textbf{R} \limp \textbf{S} \;\;\vdash \;\; \textbf{T}}{\textbf{H},\; \textbf{Q},\; \textbf{P} \land \ldots \land \textbf{Q} \land \ldots \land \textbf{R} \limp \textbf{S} \;\;\vdash \;\; \textbf{T} }</math> || || A | {{RRRow}}|*||<font size="-2"> IMP_L1 </font>|| <math>\frac{\textbf{H},\; \textbf{Q},\; \textbf{P} \land \ldots \land \textbf{R} \limp \textbf{S} \;\;\vdash \;\; \textbf{T}}{\textbf{H},\; \textbf{Q},\; \textbf{P} \land \ldots \land \textbf{Q} \land \ldots \land \textbf{R} \limp \textbf{S} \;\;\vdash \;\; \textbf{T} }</math> || || A | ||
{{RRRow}}|<font size="-2"> IMP_R </font>|| <math>\frac{\textbf{H}, \textbf{P} \;\;\vdash \;\; \textbf{Q}}{\textbf{H} \;\;\vdash \;\; \textbf{P} \limp \textbf{Q}}</math> || || A | {{RRRow}}|*||<font size="-2"> IMP_R </font>|| <math>\frac{\textbf{H}, \textbf{P} \;\;\vdash \;\; \textbf{Q}}{\textbf{H} \;\;\vdash \;\; \textbf{P} \limp \textbf{Q}}</math> || || A | ||
{{RRRow}}|<font size="-2"> IMP_AND_L </font>|| <math>\frac{\textbf{H},\textbf{P} \limp \textbf{Q}, \textbf{P} \limp \textbf{R}\;\;\vdash \;\; \textbf{S}}{\textbf{H},\;\textbf{P} \limp \textbf{Q} \land \textbf{R} \;\;\vdash \;\; \textbf{S}}</math> || || A | {{RRRow}}|*||<font size="-2"> IMP_AND_L </font>|| <math>\frac{\textbf{H},\textbf{P} \limp \textbf{Q}, \textbf{P} \limp \textbf{R}\;\;\vdash \;\; \textbf{S}}{\textbf{H},\;\textbf{P} \limp \textbf{Q} \land \textbf{R} \;\;\vdash \;\; \textbf{S}}</math> || || A | ||
{{RRRow}}|<font size="-2"> IMP_OR_L </font>|| <math>\frac{ | {{RRRow}}|*||<font size="-2"> IMP_OR_L </font>|| <math>\frac{ | ||
\textbf{H},\textbf{P} \limp \textbf{R}, \textbf{Q} \limp \textbf{R}\;\;\vdash \;\; \textbf{S} }{\textbf{H},\;\textbf{P} \lor \textbf{Q} \limp \textbf{R} \;\;\vdash \;\; \textbf{S}}</math> || || A | \textbf{H},\textbf{P} \limp \textbf{R}, \textbf{Q} \limp \textbf{R}\;\;\vdash \;\; \textbf{S} }{\textbf{H},\;\textbf{P} \lor \textbf{Q} \limp \textbf{R} \;\;\vdash \;\; \textbf{S}}</math> || || A | ||
{{RRRow}}|<font size="-2"> NEG_IN_L </font>|| <math>\frac{\textbf{H},\; E \in \{ a,\ldots , c\} \; \; \vdash \; \; \; \; \textbf{P} }{\textbf{H},\; E \in \{ a,\ldots , b, \ldots , c\} , \neg \, (E=b) \; \; \vdash \; \; \textbf{P} }</math> || || A | {{RRRow}}|*||<font size="-2"> NEG_IN_L </font>|| <math>\frac{\textbf{H},\; E \in \{ a,\ldots , c\} \; \; \vdash \; \; \; \; \textbf{P} }{\textbf{H},\; E \in \{ a,\ldots , b, \ldots , c\} , \neg \, (E=b) \; \; \vdash \; \; \textbf{P} }</math> || || A | ||
{{RRRow}}|<font size="-2"> NEG_IN_R </font>|| <math>\frac{\textbf{H},\; E \in \{ a,\ldots , c\} \; \; \vdash \; \; \; \; \textbf{P} }{\textbf{H},\; E \in \{ a,\ldots , b, \ldots , c\} , \neg \, (b=E) \; \; \vdash \; \; \textbf{P} }</math> || || A | {{RRRow}}|*||<font size="-2"> NEG_IN_R </font>|| <math>\frac{\textbf{H},\; E \in \{ a,\ldots , c\} \; \; \vdash \; \; \; \; \textbf{P} }{\textbf{H},\; E \in \{ a,\ldots , b, \ldots , c\} , \neg \, (b=E) \; \; \vdash \; \; \textbf{P} }</math> || || A | ||
{{RRRow}}|<font size="-2"> XST_L </font>|| <math>\frac{\textbf{H},\; \textbf{P(x)} \; \; \vdash \; \; \textbf{Q} | {{RRRow}}|*||<font size="-2"> XST_L </font>|| <math>\frac{\textbf{H},\; \textbf{P(x)} \; \; \vdash \; \; \textbf{Q} | ||
}{ | }{ | ||
\textbf{H},\; \exists \, \textbf{x}\, \qdot\, \textbf{P(x)} \; \; \vdash \; \; \textbf{Q} | \textbf{H},\; \exists \, \textbf{x}\, \qdot\, \textbf{P(x)} \; \; \vdash \; \; \textbf{Q} | ||
}</math> || || A | }</math> || || A | ||
{{RRRow}}|<font size="-2"> ALL_R </font>|| <math>\frac{\textbf{H}\; \; \vdash \; \; \textbf{P(x)} }{ \textbf{H} \; \; \vdash \; \; \forall \textbf{x}\, \qdot\, \textbf{P(x)} }</math> || || A | {{RRRow}}|*||<font size="-2"> ALL_R </font>|| <math>\frac{\textbf{H}\; \; \vdash \; \; \textbf{P(x)} }{ \textbf{H} \; \; \vdash \; \; \forall \textbf{x}\, \qdot\, \textbf{P(x)} }</math> || || A | ||
{{RRRow}}|<font size="-2"> EQL_LR </font>|| <math>\frac{\textbf{H(E)} \; \; \vdash \; \; \; \; \textbf{P(E)} }{\textbf{H(x)},\; x=E \; \; \vdash \; \; \textbf{P(x)} }</math> || <math>x</math> is a variable which is not free in <math>E</math> || A | {{RRRow}}|*||<font size="-2"> EQL_LR </font>|| <math>\frac{\textbf{H(E)} \; \; \vdash \; \; \; \; \textbf{P(E)} }{\textbf{H(x)},\; x=E \; \; \vdash \; \; \textbf{P(x)} }</math> || <math>x</math> is a variable which is not free in <math>E</math> || A | ||
{{RRRow}}|<font size="-2"> EQL_RL </font>|| <math>\frac{\textbf{H(E)} \; \; \vdash \; \; \; \; \textbf{P(E)} }{\textbf{H(x)},\; E=x \; \; \vdash \; \; \textbf{P(x)} }</math> || <math>x</math> is a variable which is not free in <math>E</math> || A | {{RRRow}}|*||<font size="-2"> EQL_RL </font>|| <math>\frac{\textbf{H(E)} \; \; \vdash \; \; \; \; \textbf{P(E)} }{\textbf{H(x)},\; E=x \; \; \vdash \; \; \textbf{P(x)} }</math> || <math>x</math> is a variable which is not free in <math>E</math> || A | ||
{{RRRow}}|<font size="-2"> SUBSET_INTER </font>|| <math>\frac{\textbf{H},\;\textbf{T} \subseteq \textbf{U} \;\;\vdash \;\; | {{RRRow}}| ||<font size="-2"> SUBSET_INTER </font>|| <math>\frac{\textbf{H},\;\textbf{T} \subseteq \textbf{U} \;\;\vdash \;\; | ||
\textbf{G}(\textbf{S} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{V})} | \textbf{G}(\textbf{S} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{V})} | ||
{\textbf{H},\;\textbf{T} \subseteq \textbf{U} \;\;\vdash \;\; | {\textbf{H},\;\textbf{T} \subseteq \textbf{U} \;\;\vdash \;\; | ||
\textbf{G}(\textbf{S} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{U} \binter \dots \binter \textbf{V})}</math> || the <math>\binter</math> operator must appear at the "top level" || A | \textbf{G}(\textbf{S} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{U} \binter \dots \binter \textbf{V})}</math> || the <math>\binter</math> operator must appear at the "top level" || A | ||
{{RRRow}}|<font size="-2"> IN_INTER </font>|| <math>\frac{\textbf{H},\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | {{RRRow}}| ||<font size="-2"> IN_INTER </font>|| <math>\frac{\textbf{H},\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | ||
\textbf{G}(\textbf{S} \binter \dots \binter \{\textbf{E}\} \binter \dots \binter \textbf{U})} | \textbf{G}(\textbf{S} \binter \dots \binter \{\textbf{E}\} \binter \dots \binter \textbf{U})} | ||
{\textbf{H},\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | {\textbf{H},\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | ||
\textbf{G}(\textbf{S} \binter \dots \binter \{\textbf{E}\} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{U})}</math> || the <math>\binter</math> operator must appear at the "top level" || A | \textbf{G}(\textbf{S} \binter \dots \binter \{\textbf{E}\} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{U})}</math> || the <math>\binter</math> operator must appear at the "top level" || A | ||
{{RRRow}}|<font size="-2"> NOTIN_INTER </font>|| <math>\frac{\textbf{H},\;\lnot\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | {{RRRow}}| ||<font size="-2"> NOTIN_INTER </font>|| <math>\frac{\textbf{H},\;\lnot\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | ||
\textbf{G}(\emptyset)} | \textbf{G}(\emptyset)} | ||
{\textbf{H},\;\lnot\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | {\textbf{H},\;\lnot\;\textbf{E} \in \textbf{T} \;\;\vdash \;\; | ||
\textbf{G}(\textbf{S} \binter \dots \binter \{\textbf{E}\} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{U})}</math> || the <math>\binter</math> operator must appear at the "top level" || A | \textbf{G}(\textbf{S} \binter \dots \binter \{\textbf{E}\} \binter \dots \binter \textbf{T} \binter \dots \binter \textbf{U})}</math> || the <math>\binter</math> operator must appear at the "top level" || A | ||
{{RRRow}}|<font size="-2"> CASE </font>|| <math>\frac{\textbf{H}, \; \textbf{P} \; \; \vdash \; \; \textbf{R} \ \ \ \ \ldots \ \ \ \ \textbf{H}, \; \textbf{Q} \; \; \vdash \; \; \textbf{R} }{\textbf{H},\; \textbf{P} \lor \ldots \lor \textbf{Q} \; \; \vdash \; \; \textbf{R} }</math> || || M | {{RRRow}}|*||<font size="-2"> CASE </font>|| <math>\frac{\textbf{H}, \; \textbf{P} \; \; \vdash \; \; \textbf{R} \ \ \ \ \ldots \ \ \ \ \textbf{H}, \; \textbf{Q} \; \; \vdash \; \; \textbf{R} }{\textbf{H},\; \textbf{P} \lor \ldots \lor \textbf{Q} \; \; \vdash \; \; \textbf{R} }</math> || || M | ||
{{RRRow}}|<font size="-2"> MH </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;\textbf{P} \qquad \textbf{H},\;\textbf{P},\; \textbf{Q} \;\;\vdash \;\; \textbf{R} }{\textbf{H},\;\textbf{P} \limp \textbf{Q} \;\;\vdash \;\; \textbf{R} \ \ \ \ \ }</math> || || M | {{RRRow}}|*||<font size="-2"> MH </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;\textbf{P} \qquad \textbf{H},\;\textbf{P},\; \textbf{Q} \;\;\vdash \;\; \textbf{R} }{\textbf{H},\;\textbf{P} \limp \textbf{Q} \;\;\vdash \;\; \textbf{R} \ \ \ \ \ }</math> || || M | ||
{{RRRow}}|<font size="-2"> HM </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;\neg\,\textbf{Q} \qquad \textbf{H},\;\neg\,\textbf{Q},\; \neg\,\textbf{P} \;\;\vdash \;\; \textbf{R} }{\textbf{H},\;\textbf{P} \limp \textbf{Q} \;\;\vdash \;\; \textbf{R} \ \ \ \ \ }</math> || || M | {{RRRow}}|*||<font size="-2"> HM </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;\neg\,\textbf{Q} \qquad \textbf{H},\;\neg\,\textbf{Q},\; \neg\,\textbf{P} \;\;\vdash \;\; \textbf{R} }{\textbf{H},\;\textbf{P} \limp \textbf{Q} \;\;\vdash \;\; \textbf{R} \ \ \ \ \ }</math> || || M | ||
{{RRRow}}|<font size="-2"> EQV </font>|| <math>\frac{\textbf{H(Q)}, \textbf{P} \leqv \textbf{Q} | {{RRRow}}|*||<font size="-2"> EQV </font>|| <math>\frac{\textbf{H(Q)}, \textbf{P} \leqv \textbf{Q} | ||
\;\;\vdash\;\; \textbf{G(Q)}}{\textbf{H(P)},\;\textbf{P} \leqv \textbf{Q} | \;\;\vdash\;\; \textbf{G(Q)}}{\textbf{H(P)},\;\textbf{P} \leqv \textbf{Q} | ||
\;\;\vdash \;\; \textbf{G(P)} \ \ \ \ \ }</math> || || M | \;\;\vdash \;\; \textbf{G(P)} \ \ \ \ \ }</math> || || M | ||
{{RRRow}}|<font size="-2"> OV_L </font>|| <math>\frac{\textbf{H},\; G=E | {{RRRow}}|*||<font size="-2"> OV_L </font>|| <math>\frac{\textbf{H},\; G=E | ||
,\;\textbf{P}(F)\;\;\vdash\;\;\textbf{Q} \qquad \textbf{H},\; \neg\,(G=E) | ,\;\textbf{P}(F)\;\;\vdash\;\;\textbf{Q} \qquad \textbf{H},\; \neg\,(G=E) | ||
,\;\textbf{P}(f(G))\;\;\vdash\;\;\textbf{Q}}{\textbf{H},\;\textbf{P}((f\ovl\{E | ,\;\textbf{P}(f(G))\;\;\vdash\;\;\textbf{Q}}{\textbf{H},\;\textbf{P}((f\ovl\{E | ||
\mapsto F\})(G)) \;\;\vdash \;\; \textbf{Q}}</math> || the <math>\ovl</math> operator must appear at the "top level" || M | \mapsto F\})(G)) \;\;\vdash \;\; \textbf{Q}}</math> || the <math>\ovl</math> operator must appear at the "top level" || M | ||
{{RRRow}}|<font size="-2"> OV_R </font>|| <math>\frac{\textbf{H},\; G=E \;\;\vdash\;\;\textbf{Q}(F) | {{RRRow}}|*||<font size="-2"> OV_R </font>|| <math>\frac{\textbf{H},\; G=E \;\;\vdash\;\;\textbf{Q}(F) | ||
\qquad \textbf{H},\; \neg\,(G=E) \;\;\vdash\;\;\textbf{Q}(f(G))}{\textbf{H} | \qquad \textbf{H},\; \neg\,(G=E) \;\;\vdash\;\;\textbf{Q}(f(G))}{\textbf{H} | ||
\;\;\vdash \;\; \textbf{Q}((f\ovl\{E \mapsto F\})(G)) \ \ \ \ \ }</math> || the <math>\ovl</math> operator must appear at the "top level" || M | \;\;\vdash \;\; \textbf{Q}((f\ovl\{E \mapsto F\})(G)) \ \ \ \ \ }</math> || the <math>\ovl</math> operator must appear at the "top level" || M | ||
{{RRRow}}|<font size="-2"> OV_L </font>|| <math>\frac{\textbf{H},\; G \in \dom(g) ,\;\textbf{P}(g(G))\;\;\vdash\;\;\textbf{Q} \qquad \textbf{H},\; \neg\,G \in \dom(g) ,\;\textbf{P}(f(G))\;\;\vdash\;\;\textbf{Q}}{\textbf{H},\;\textbf{P}((f\ovl g)(G)) \;\;\vdash \;\; \textbf{Q} \ \ \ \ \ }</math> || the <math>\ovl</math> operator must appear at the "top level" || M | {{RRRow}}|*||<font size="-2"> OV_L </font>|| <math>\frac{\textbf{H},\; G \in \dom(g) ,\;\textbf{P}(g(G))\;\;\vdash\;\;\textbf{Q} \qquad \textbf{H},\; \neg\,G \in \dom(g) ,\;\textbf{P}(f(G))\;\;\vdash\;\;\textbf{Q}}{\textbf{H},\;\textbf{P}((f\ovl g)(G)) \;\;\vdash \;\; \textbf{Q} \ \ \ \ \ }</math> || the <math>\ovl</math> operator must appear at the "top level" || M | ||
{{RRRow}}|<font size="-2"> OV_R </font>|| <math>\frac{\textbf{H},\; G \in \dom(g) \;\;\vdash\;\;\textbf{Q}(g(G)) \qquad \textbf{H},\; \neg\, G \in \dom(g) \;\;\vdash\;\;\textbf{Q}(f(G))}{\textbf{H} \;\;\vdash \;\; \textbf{Q}((f\ovl g)(G)) \ \ \ \ \ }</math> || the <math>\ovl</math> operator must appear at the "top level" || M | {{RRRow}}|*||<font size="-2"> OV_R </font>|| <math>\frac{\textbf{H},\; G \in \dom(g) \;\;\vdash\;\;\textbf{Q}(g(G)) \qquad \textbf{H},\; \neg\, G \in \dom(g) \;\;\vdash\;\;\textbf{Q}(f(G))}{\textbf{H} \;\;\vdash \;\; \textbf{Q}((f\ovl g)(G)) \ \ \ \ \ }</math> || the <math>\ovl</math> operator must appear at the "top level" || M | ||
{{RRRow}}|<font size="-2"> DIS_BINTER_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \binter f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \binter T]) \ \ \ \ \ }</math> || the occurrence of <math>f^{-1}</math> must appear at the "top level". Moreover <math>A</math> and <math>B</math> denote some type. Similar left distribution rules exist || M | {{RRRow}}|*||<font size="-2"> DIS_BINTER_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \binter f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \binter T]) \ \ \ \ \ }</math> || the occurrence of <math>f^{-1}</math> must appear at the "top level". Moreover <math>A</math> and <math>B</math> denote some type. Similar left distribution rules exist || M | ||
{{RRRow}}|<font size="-2"> DIS_SETMINUS_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\; f \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f^{-1}[S] \setminus f^{-1}[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f^{-1}[S \setminus T]) \ \ \ \ \ }</math> || the occurrence of <math>f^{-1}</math> must appear at the "top level". Moreover <math>A</math> and <math>B</math> denote some type. Similar left distribution rules exist || M | {{RRRow}}|*||<font size="-2"> DIS_SETMINUS_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\; f \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f^{-1}[S] \setminus f^{-1}[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f^{-1}[S \setminus T]) \ \ \ \ \ }</math> || the occurrence of <math>f^{-1}</math> must appear at the "top level". Moreover <math>A</math> and <math>B</math> denote some type. Similar left distribution rules exist || M | ||
{{RRRow}}|<font size="-2"> SIM_REL_IMAGE_R </font>|| <math>\frac{\textbf{H} \; \; \vdash \; \; {WD}(\textbf{Q}(\{ f(E)\} )) \qquad\textbf{H} \; \; \vdash \; \; \textbf{Q}(\{ f(E)\} ) }{\textbf{H} \; \; \vdash \; \; \textbf{Q}(f[\{ E\} ])} </math> || the occurrence of <math>f</math> must appear at the "top level". A similar left simplification rule exists. || M | {{RRRow}}|*||<font size="-2"> SIM_REL_IMAGE_R </font>|| <math>\frac{\textbf{H} \; \; \vdash \; \; {WD}(\textbf{Q}(\{ f(E)\} )) \qquad\textbf{H} \; \; \vdash \; \; \textbf{Q}(\{ f(E)\} ) }{\textbf{H} \; \; \vdash \; \; \textbf{Q}(f[\{ E\} ])} </math> || the occurrence of <math>f</math> must appear at the "top level". A similar left simplification rule exists. || M | ||
{{RRRow}}|<font size="-2"> SIM_FCOMP_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;{WD}(\textbf{Q}(g(f(x)))) \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(g(f(x))) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}((f \fcomp g)(x)) \ \ \ \ \ }</math> || the occurrence of <math>f \fcomp g</math> must appear at the "top level". A similar left simplification rule exists. || M | {{RRRow}}|*||<font size="-2"> SIM_FCOMP_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;{WD}(\textbf{Q}(g(f(x)))) \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(g(f(x))) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}((f \fcomp g)(x)) \ \ \ \ \ }</math> || the occurrence of <math>f \fcomp g</math> must appear at the "top level". A similar left simplification rule exists. || M | ||
{{RRRow}}|<font size="-2"> FIN_SUBSETEQ_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; S \subseteq T \qquad; \textbf{H} \;\;\vdash \;\; \finite\,(T)}{\textbf{H} \;\;\vdash \;\; \finite\,(S) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_SUBSETEQ_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; S \subseteq T \qquad; \textbf{H} \;\;\vdash \;\; \finite\,(T)}{\textbf{H} \;\;\vdash \;\; \finite\,(S) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_BINTER_R </font>|| <math>\frac{\textbf{H} \;\;\vdash | {{RRRow}}|*||<font size="-2"> FIN_BINTER_R </font>|| <math>\frac{\textbf{H} \;\;\vdash | ||
\;\;\finite\,(S) \;\lor\;\ldots \;\lor\; \finite\,(T)}{\textbf{H} \;\;\vdash | \;\;\finite\,(S) \;\lor\;\ldots \;\lor\; \finite\,(T)}{\textbf{H} \;\;\vdash | ||
\;\; \finite\,(S \;\binter\;\ldots \;\binter\; T)}</math> || || M | \;\; \finite\,(S \;\binter\;\ldots \;\binter\; T)}</math> || || M | ||
{{RRRow}}|<font size="-2"> FIN_SETMINUS_R </font>|| <math>\frac{\textbf{H} \;\;\vdash | {{RRRow}}|*||<font size="-2"> FIN_SETMINUS_R </font>|| <math>\frac{\textbf{H} \;\;\vdash | ||
\;\;\finite\,(S)}{\textbf{H} \;\;\vdash \;\; \finite\,(S \;\setminus\; T) \ \ \ \ \ \ \ }</math> || || M | \;\;\finite\,(S)}{\textbf{H} \;\;\vdash \;\; \finite\,(S \;\setminus\; T) \ \ \ \ \ \ \ }</math> || || M | ||
{{RRRow}}|<font size="-2"> FIN_REL_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; r \;\in\; S \rel T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) \qquad \textbf{H} \;\;\vdash \;\; \finite\,(T)}{\textbf{H} \;\;\vdash \;\; \finite\,(r)}</math> || the user has to write the set corresponding to <math>S \rel T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_REL_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; r \;\in\; S \rel T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) \qquad \textbf{H} \;\;\vdash \;\; \finite\,(T)}{\textbf{H} \;\;\vdash \;\; \finite\,(r)}</math> || the user has to write the set corresponding to <math>S \rel T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_REL_IMG_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(r[s]) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_REL_IMG_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(r[s]) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_REL_RAN_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(\ran(r)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_REL_RAN_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(\ran(r)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_REL_DOM_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(\dom(r)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_REL_DOM_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(\dom(r)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_FUN1_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(f) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_FUN1_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(f) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_FUN2_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f^{-1} \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(f) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_FUN2_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f^{-1} \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(f) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_FUN_IMG_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(s) }{\textbf{H} \;\;\vdash \;\; \finite\,(f[s]) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_FUN_IMG_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(s) }{\textbf{H} \;\;\vdash \;\; \finite\,(f[s]) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_FUN_RAN_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(\ran(f)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_FUN_RAN_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(\ran(f)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> FIN_FUN_DOM_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f^{-1} \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(\dom(f)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_FUN_DOM_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; f^{-1} \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(S) }{\textbf{H} \;\;\vdash \;\; \finite\,(\dom(f)) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>S \pfun T</math> in the editing area of the Proof Control Window || M | ||
{{RRRow}}|<font size="-2"> LOWER_BOUND_L </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \leq x)}</math> || <math>S</math> must not contain any bound variable || M | {{RRRow}}|*||<font size="-2"> LOWER_BOUND_L </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \leq x)}</math> || <math>S</math> must not contain any bound variable || M | ||
{{RRRow}}|<font size="-2"> LOWER_BOUND_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \geq n)}</math> || <math>S</math> must not contain any bound variable || M | {{RRRow}}|*||<font size="-2"> LOWER_BOUND_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \geq n)}</math> || <math>S</math> must not contain any bound variable || M | ||
{{RRRow}}|<font size="-2"> UPPER_BOUND_L </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \geq x)}</math> || <math>S</math> must not contain any bound variable || M | {{RRRow}}|*||<font size="-2"> UPPER_BOUND_L </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \geq x)}</math> || <math>S</math> must not contain any bound variable || M | ||
{{RRRow}}|<font size="-2"> UPPER_BOUND_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \leq n)}</math> || <math>S</math> must not contain any bound variable || M | {{RRRow}}|*||<font size="-2"> UPPER_BOUND_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \finite(S) }{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \leq n)}</math> || <math>S</math> must not contain any bound variable || M | ||
{{RRRow}}|<font size="-2"> FIN_LT_0 </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \leq x) \qquad \textbf{H} \;\;\vdash \;\; S \subseteq \intg \setminus \natn }{\textbf{H} \;\;\vdash \;\; \finite(S)}</math> || || M | {{RRRow}}|*||<font size="-2"> FIN_LT_0 </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \leq x) \qquad \textbf{H} \;\;\vdash \;\; S \subseteq \intg \setminus \natn }{\textbf{H} \;\;\vdash \;\; \finite(S)}</math> || || M | ||
{{RRRow}}|<font size="-2"> FIN_GE_0 </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \leq n) \qquad \textbf{H} \;\;\vdash \;\; S \subseteq \nat }{\textbf{H} \;\;\vdash \;\; \finite(S)}</math> || || M | {{RRRow}}|*||<font size="-2"> FIN_GE_0 </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \leq n) \qquad \textbf{H} \;\;\vdash \;\; S \subseteq \nat }{\textbf{H} \;\;\vdash \;\; \finite(S)}</math> || || M | ||
{{RRRow}}|<font size="-2"> CARD_INTERV </font>|| <math>\frac{\textbf{H},\, a \leq b \;\;\vdash \;\; \textbf{Q}(b-a+1) \qquad \textbf{H},\, b < a \;\;\vdash \;\; \textbf{Q}(0) }{\textbf{H} \;\;\vdash\;\; \textbf{Q}(\card\,(a\upto b))}</math> || <math>\card (a \upto b)</math> must appear at "top-level" || M | {{RRRow}}|*||<font size="-2"> CARD_INTERV </font>|| <math>\frac{\textbf{H},\, a \leq b \;\;\vdash \;\; \textbf{Q}(b-a+1) \qquad \textbf{H},\, b < a \;\;\vdash \;\; \textbf{Q}(0) }{\textbf{H} \;\;\vdash\;\; \textbf{Q}(\card\,(a\upto b))}</math> || <math>\card (a \upto b)</math> must appear at "top-level" || M | ||
{{RRRow}}|<font size="-2"> CARD_EMPTY_INTERV </font>|| <math>\frac{\textbf{H},\, a \leq b,\,\textbf{P}(a-b+1) \;\;\vdash \;\; \textbf{Q} \qquad \textbf{H},\, b < a ,\, \textbf{P}(0)\;\;\vdash \;\; \textbf{Q} }{\textbf{H},\,\textbf{P}(\card\,(a\upto b)) \;\;\vdash\;\; \textbf{Q}}</math> || <math>\card (a \upto b)</math> must appear at "top-level" || M | {{RRRow}}|*||<font size="-2"> CARD_EMPTY_INTERV </font>|| <math>\frac{\textbf{H},\, a \leq b,\,\textbf{P}(a-b+1) \;\;\vdash \;\; \textbf{Q} \qquad \textbf{H},\, b < a ,\, \textbf{P}(0)\;\;\vdash \;\; \textbf{Q} }{\textbf{H},\,\textbf{P}(\card\,(a\upto b)) \;\;\vdash\;\; \textbf{Q}}</math> || <math>\card (a \upto b)</math> must appear at "top-level" || M | ||
{{RRRow}}|<font size="-2"> CARD_SUBSETEQ </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \textbf{P}(S \subseteq T) }{\textbf{H} \;\;\vdash\;\; \textbf{P}(\card\,(S) \leq \card(T))}</math> || || M | {{RRRow}}|*||<font size="-2"> CARD_SUBSETEQ </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; \textbf{P}(S \subseteq T) }{\textbf{H} \;\;\vdash\;\; \textbf{P}(\card\,(S) \leq \card(T))}</math> || || M | ||
|} | |} | ||
Revision as of 18:08, 11 February 2009
Conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Inference_rules
| Name | Rule | Side Condition | A/M
| |
|---|---|---|---|---|
| * | HYP | 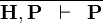 |
A
| |
| * | HYP_OR | 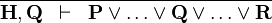 |
A
| |
| * | CNTR | 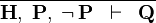 |
A
| |
| * | FALSE_HYP | 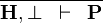 |
A
| |
| * | TRUE_GOAL | 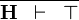 |
A
| |
| * | DBL_HYP | 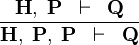 |
A
| |
| * | AND_L | 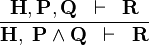 |
A
| |
| * | AND_R | 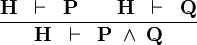 |
A
| |
| * | IMP_L1 | 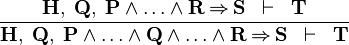 |
A
| |
| * | IMP_R | 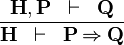 |
A
| |
| * | IMP_AND_L | 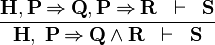 |
A
| |
| * | IMP_OR_L | 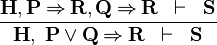 |
A
| |
| * | NEG_IN_L | 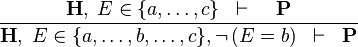 |
A
| |
| * | NEG_IN_R | 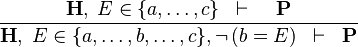 |
A
| |
| * | XST_L | 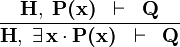 |
A
| |
| * | ALL_R | 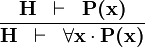 |
A
| |
| * | EQL_LR |  |
 is a variable which is not free in is a variable which is not free in  |
A
|
| * | EQL_RL | 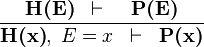 |
 is a variable which is not free in is a variable which is not free in  |
A
|
| SUBSET_INTER | 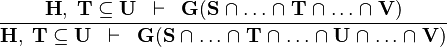 |
the 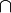 operator must appear at the "top level" operator must appear at the "top level" |
A
| |
| IN_INTER | 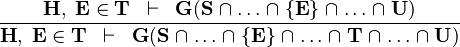 |
the 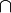 operator must appear at the "top level" operator must appear at the "top level" |
A
| |
| NOTIN_INTER | 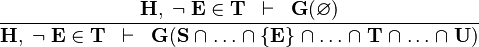 |
the 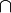 operator must appear at the "top level" operator must appear at the "top level" |
A
| |
| * | CASE |  |
M
| |
| * | MH | 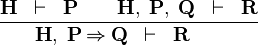 |
M
| |
| * | HM | 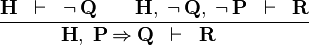 |
M
| |
| * | EQV | 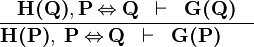 |
M
| |
| * | OV_L | 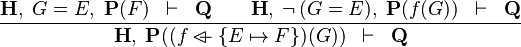 |
the 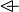 operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | OV_R | 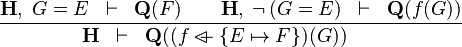 |
the 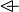 operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | OV_L | 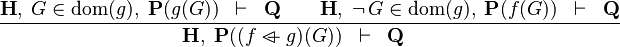 |
the 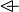 operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | OV_R | 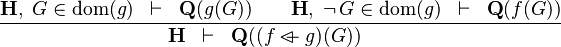 |
the 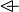 operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | DIS_BINTER_R | ![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \binter f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \binter T]) \ \ \ \ \ }](/images/math/5/3/8/538882eb3fc5acd65e54da755e9513ae.png) |
the occurrence of 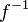 must appear at the "top level". Moreover must appear at the "top level". Moreover 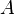 and and 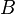 denote some type. Similar left distribution rules exist denote some type. Similar left distribution rules exist |
M
|
| * | DIS_SETMINUS_R | ![\frac{\textbf{H} \;\;\vdash\;\; f \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f^{-1}[S] \setminus f^{-1}[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f^{-1}[S \setminus T]) \ \ \ \ \ }](/images/math/7/b/0/7b04e53df06f010824217b1e9aed63da.png) |
the occurrence of 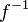 must appear at the "top level". Moreover must appear at the "top level". Moreover 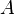 and and 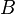 denote some type. Similar left distribution rules exist denote some type. Similar left distribution rules exist |
M
|
| * | SIM_REL_IMAGE_R | ![\frac{\textbf{H} \; \; \vdash \; \; {WD}(\textbf{Q}(\{ f(E)\} )) \qquad\textbf{H} \; \; \vdash \; \; \textbf{Q}(\{ f(E)\} ) }{\textbf{H} \; \; \vdash \; \; \textbf{Q}(f[\{ E\} ])}](/images/math/7/d/f/7dfac56e8c4269e247b888bd790b211d.png) |
the occurrence of 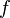 must appear at the "top level". A similar left simplification rule exists. must appear at the "top level". A similar left simplification rule exists. |
M
|
| * | SIM_FCOMP_R | 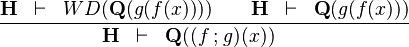 |
the occurrence of 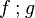 must appear at the "top level". A similar left simplification rule exists. must appear at the "top level". A similar left simplification rule exists. |
M
|
| * | FIN_SUBSETEQ_R | 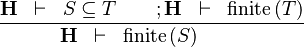 |
the user has to write the set corresponding to  in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_BINTER_R | 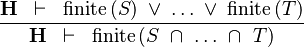 |
M
| |
| * | FIN_SETMINUS_R | 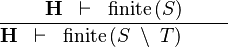 |
M
| |
| * | FIN_REL_R | 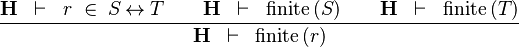 |
the user has to write the set corresponding to 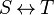 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_IMG_R | ![\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(r[s]) \ \ \ \ \ \ \ }](/images/math/7/d/1/7d1b728949ca9ee920276cc4d7b89997.png) |
the user has to write the set corresponding to 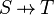 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_RAN_R | 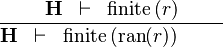 |
the user has to write the set corresponding to 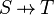 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_DOM_R | 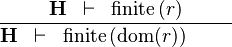 |
the user has to write the set corresponding to 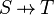 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN1_R | 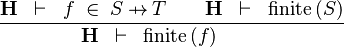 |
the user has to write the set corresponding to 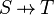 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN2_R | 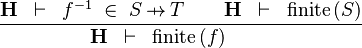 |
the user has to write the set corresponding to 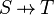 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_IMG_R | ![\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(s) }{\textbf{H} \;\;\vdash \;\; \finite\,(f[s]) \ \ \ \ \ \ \ }](/images/math/c/1/3/c13b905d1407ea16b0e2c7c7e2d3309b.png) |
the user has to write the set corresponding to 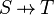 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_RAN_R | 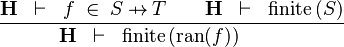 |
the user has to write the set corresponding to 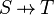 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_DOM_R | 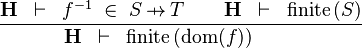 |
the user has to write the set corresponding to 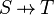 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | LOWER_BOUND_L | 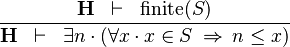 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | LOWER_BOUND_R | 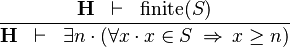 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | UPPER_BOUND_L | 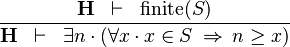 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | UPPER_BOUND_R | 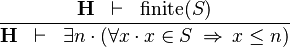 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | FIN_LT_0 | 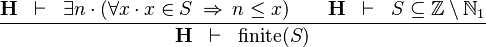 |
M
| |
| * | FIN_GE_0 | 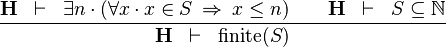 |
M
| |
| * | CARD_INTERV | 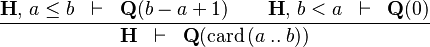 |
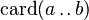 must appear at "top-level" must appear at "top-level" |
M
|
| * | CARD_EMPTY_INTERV | 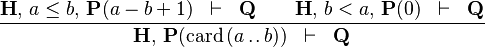 |
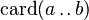 must appear at "top-level" must appear at "top-level" |
M
|
| * | CARD_SUBSETEQ | 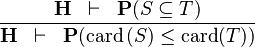 |
M |