Inference Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Laurent mNo edit summary |
imported>Laurent m Renamed SIM_FUN into FUN_GOAL. |
||
| Line 12: | Line 12: | ||
{{RRRow}}|*||<font size="-2"> TRUE_GOAL </font>|| <math>\frac{}{\textbf{H} \;\;\vdash \;\; \btrue}</math> || || A | {{RRRow}}|*||<font size="-2"> TRUE_GOAL </font>|| <math>\frac{}{\textbf{H} \;\;\vdash \;\; \btrue}</math> || || A | ||
{{RRRow}}|*||<font size="-2"> FUN_GOAL </font>|| <math>\frac{}{\textbf{H},\; f\in A\;\mathit{op}\; B \;\;\vdash\;\; f\in T_1\pfun T_2}</math> || where <math>T_1</math> and <math>T_2</math> denote types and <math>\mathit{op}</math> is one of <math>\pfun</math>, <math>\tfun</math>, <math>\pinj</math>, <math>\tinj</math>, <math>\psur</math>, <math>\tsur</math>, <math>\tbij</math>. || A | |||
{{RRRow}}|*||<font size="-2"> DBL_HYP </font>|| <math>\frac{\textbf{H},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}{\textbf{H},\;\textbf{P},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}</math> || || A | {{RRRow}}|*||<font size="-2"> DBL_HYP </font>|| <math>\frac{\textbf{H},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}{\textbf{H},\;\textbf{P},\;\textbf{P} \;\;\vdash \;\; \textbf{Q}}</math> || || A | ||
| Line 93: | Line 95: | ||
{{RRRow}}|*||<font size="-2"> SIM_FCOMP_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;{WD}(\textbf{Q}(g(f(x)))) \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(g(f(x))) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}((f \fcomp g)(x)) \ \ \ \ \ }</math> || the occurrence of <math>f \fcomp g</math> must appear at the "top level". A similar left simplification rule exists. || M | {{RRRow}}|*||<font size="-2"> SIM_FCOMP_R </font>|| <math>\frac{\textbf{H} \;\;\vdash\;\;{WD}(\textbf{Q}(g(f(x)))) \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(g(f(x))) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}((f \fcomp g)(x)) \ \ \ \ \ }</math> || the occurrence of <math>f \fcomp g</math> must appear at the "top level". A similar left simplification rule exists. || M | ||
{{RRRow}}|*||<font size="-2"> FIN_SUBSETEQ_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; S \subseteq T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(T)}{\textbf{H} \;\;\vdash \;\; \finite\,(S) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>T</math> in the editing area of the Proof Control Window || M | {{RRRow}}|*||<font size="-2"> FIN_SUBSETEQ_R </font>|| <math>\frac{\textbf{H} \;\;\vdash \;\; S \subseteq T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(T)}{\textbf{H} \;\;\vdash \;\; \finite\,(S) \ \ \ \ \ \ \ }</math> || the user has to write the set corresponding to <math>T</math> in the editing area of the Proof Control Window || M | ||
Revision as of 13:21, 6 July 2009
Conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Inference_Rules
| Name | Rule | Side Condition | A/M
| |
|---|---|---|---|---|
| * | HYP | 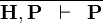 |
A
| |
| * | HYP_OR | 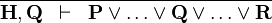 |
A
| |
| * | CNTR | 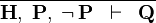 |
A
| |
| * | FALSE_HYP | 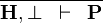 |
A
| |
| * | TRUE_GOAL | 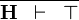 |
A
| |
| * | FUN_GOAL | 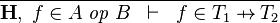 |
where 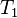 and and 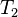 denote types and denote types and 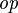 is one of is one of 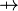 , , 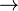 , , 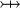 , , 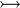 , , 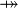 , , 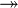 , , 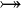 . . |
A
|
| * | DBL_HYP | 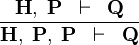 |
A
| |
| * | AND_L | 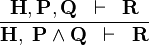 |
A
| |
| * | AND_R | 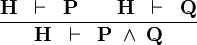 |
A
| |
| * | IMP_L1 | 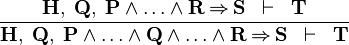 |
A
| |
| * | IMP_R | 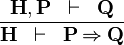 |
A
| |
| * | IMP_AND_L | 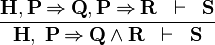 |
A
| |
| * | IMP_OR_L | 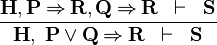 |
A
| |
| * | NEG_IN_L | 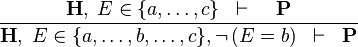 |
A
| |
| * | NEG_IN_R | 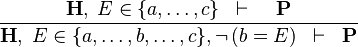 |
A
| |
| * | XST_L | 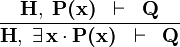 |
A
| |
| * | ALL_R | 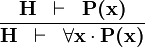 |
A
| |
| * | EQL_LR |  |
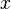 is a variable which is not free in is a variable which is not free in 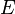 |
A
|
| * | EQL_RL | 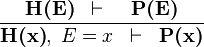 |
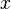 is a variable which is not free in is a variable which is not free in 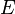 |
A
|
| SUBSET_INTER | 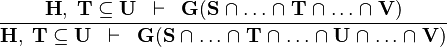 |
the  operator must appear at the "top level" operator must appear at the "top level" |
A
| |
| IN_INTER | 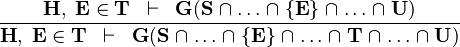 |
the  operator must appear at the "top level" operator must appear at the "top level" |
A
| |
| NOTIN_INTER | 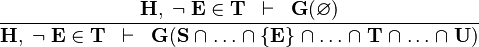 |
the  operator must appear at the "top level" operator must appear at the "top level" |
A
| |
| * | CONTRADICT_L | 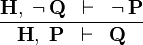 |
M
| |
| * | CONTRADICT_R | 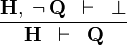 |
M
| |
| * | CASE |  |
M
| |
| * | MH | 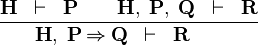 |
M
| |
| * | HM | 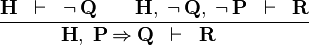 |
M
| |
| * | EQV | 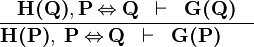 |
M
| |
| * | OV_L | 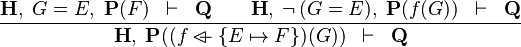 |
the  operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | OV_R | 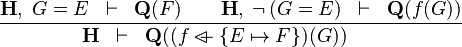 |
the  operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | OV_L | 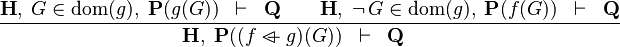 |
the  operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | OV_R | 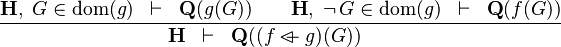 |
the  operator must appear at the "top level" operator must appear at the "top level" |
M
|
| * | DIS_BINTER_R | ![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \binter f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \binter T]) \ \ \ \ \ }](/images/math/5/3/8/538882eb3fc5acd65e54da755e9513ae.png) |
the occurrence of 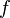 must appear at the "top level". Moreover must appear at the "top level". Moreover 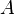 and and 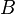 denote some type. Similar left distribution rules exist denote some type. Similar left distribution rules exist |
M
|
| * | DIS_SETMINUS_R | ![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \setminus f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \setminus T]) \ \ \ \ \ }](/images/math/8/8/a/88a3101cc210b88d5fe59746292f12fe.png) |
the occurrence of 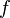 must appear at the "top level". Moreover must appear at the "top level". Moreover 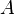 and and 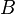 denote some type. Similar left distribution rules exist denote some type. Similar left distribution rules exist |
M
|
| * | SIM_REL_IMAGE_R | ![\frac{\textbf{H} \; \; \vdash \; \; {WD}(\textbf{Q}(\{ f(E)\} )) \qquad\textbf{H} \; \; \vdash \; \; \textbf{Q}(\{ f(E)\} ) }{\textbf{H} \; \; \vdash \; \; \textbf{Q}(f[\{ E\} ])}](/images/math/7/d/f/7dfac56e8c4269e247b888bd790b211d.png) |
the occurrence of 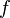 must appear at the "top level". A similar left simplification rule exists. must appear at the "top level". A similar left simplification rule exists. |
M
|
| * | SIM_FCOMP_R | 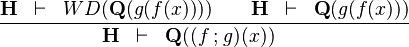 |
the occurrence of 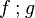 must appear at the "top level". A similar left simplification rule exists. must appear at the "top level". A similar left simplification rule exists. |
M
|
| * | FIN_SUBSETEQ_R | 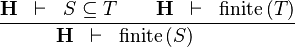 |
the user has to write the set corresponding to 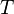 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_BINTER_R | 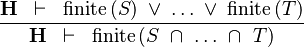 |
M
| |
| * | FIN_SETMINUS_R | 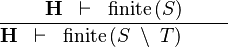 |
M
| |
| * | FIN_REL_R | 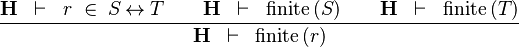 |
the user has to write the set corresponding to 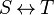 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_IMG_R | ![\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(r[s]) \ \ \ \ \ \ \ }](/images/math/7/d/1/7d1b728949ca9ee920276cc4d7b89997.png) |
the user has to write the set corresponding to 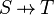 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_RAN_R | 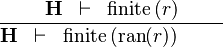 |
the user has to write the set corresponding to 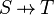 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_DOM_R | 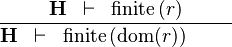 |
the user has to write the set corresponding to 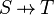 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN1_R | 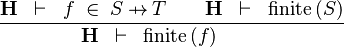 |
the user has to write the set corresponding to 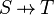 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN2_R | 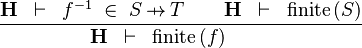 |
the user has to write the set corresponding to 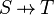 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_IMG_R | ![\frac{\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(s) }{\textbf{H} \;\;\vdash \;\; \finite\,(f[s]) \ \ \ \ \ \ \ }](/images/math/c/1/3/c13b905d1407ea16b0e2c7c7e2d3309b.png) |
the user has to write the set corresponding to 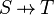 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_RAN_R | 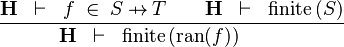 |
the user has to write the set corresponding to 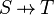 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_DOM_R | 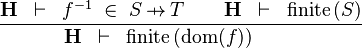 |
the user has to write the set corresponding to 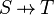 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | LOWER_BOUND_L |  |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | LOWER_BOUND_R | 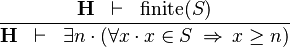 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | UPPER_BOUND_L | 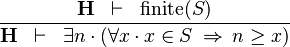 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | UPPER_BOUND_R | 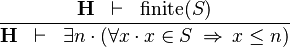 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | FIN_LT_0 | 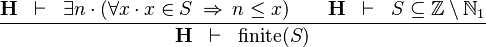 |
M
| |
| * | FIN_GE_0 |  |
M
| |
| * | CARD_INTERV | 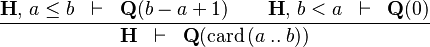 |
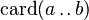 must appear at "top-level" must appear at "top-level" |
M
|
| * | CARD_EMPTY_INTERV | 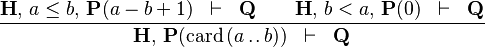 |
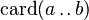 must appear at "top-level" must appear at "top-level" |
M
|
| * | CARD_SUBSETEQ | 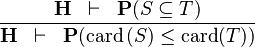 |
M
| |
| * | FORALL_INST | ![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} , [x \bcmeq E]\textbf{P} \;\;\vdash \;\; \textbf{G}}{\textbf{H}, \forall x \qdot \textbf{P} \;\;\vdash\;\; \textbf{G}}](/images/math/a/c/b/acb596a712a0f720a7d3238f967ccfe6.png) |
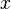 is instantiated with is instantiated with 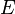 |
M
|
| * | FORALL_INST_MP | ![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H}, {WD}(E) \;\;\vdash \;\; [x \bcmeq E]\textbf{P} \qquad \textbf{H}, {WD}(E), [x \bcmeq E]\textbf{Q} \;\;\vdash \;\; \textbf{G}}{\textbf{H}, \forall x \qdot \textbf{P} \limp \textbf{Q} \;\;\vdash\;\; \textbf{G}}](/images/math/e/2/5/e25e646ecaceca4cb4143a3e66dbb185.png) |
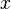 is instantiated with is instantiated with 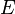 and a Modus Ponens is applied and a Modus Ponens is applied |
M
|
| * | CUT | 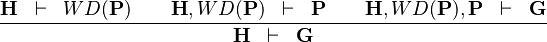 |
hypothesis  is added is added |
M
|
| * | EXISTS_INST | ![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} , [x \bcmeq E]\textbf{P} \;\;\vdash \;\; \textbf{G}}{\textbf{H}, \exists x \qdot \textbf{P} \;\;\vdash\;\; \textbf{G}}](/images/math/a/3/a/a3af36c01f37d2d738cde14ec1be4e20.png) |
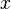 is instantiated with is instantiated with 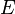 |
M
|
| * | DISTINCT_CASE | 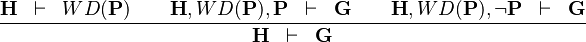 |
case distinction on predicate  |
M |