Negation Normal Form: Difference between revisions
imported>Billaude Description and implementation of the Negation Normal Form |
imported>Laurent |
||
| Line 19: | Line 19: | ||
There is no rule implemented for that type of expression : <math> \lnot (P \leqv Q) </math> (which is equivalent to <math> (\lnot P \leqv Q))</math> The way the reasoner will work is yet to be defined. Since the "<math>\leqv</math>" is to be kept, the choice on which predicate the not will be applied is ambiguous. Here is an example showing that difficulty : | There is no rule implemented for that type of expression : <math> \lnot (P \leqv Q) </math> (which is equivalent to <math> (\lnot P \leqv Q))</math> The way the reasoner will work is yet to be defined. Since the "<math>\leqv</math>" is to be kept, the choice on which predicate the not will be applied to is ambiguous. Here is an example showing that difficulty : | ||
| Line 28: | Line 28: | ||
A better solution would to apply the <math>\lnot</math> on a member containing already a <math>\lnot</math>. But it can be hard to find an expression with a <math>\lnot</math> which has already been put in its Negation Normal Form as for the right member in (2) | A better solution would to apply the <math>\lnot</math> on a member containing already a <math>\lnot</math>. But it can be hard to find an expression with a <math>\lnot</math> which has already been put in its Negation Normal Form as for the right member in (2) | ||
= Implementation = | = Implementation = | ||
Revision as of 15:43, 13 April 2011
This page describe the Negation Normal Form used in Rodin and show how it has been implemented.
Definition
A logical formula is in its Negation Normal Form if negation occurs only on atomic expression. To achieve this, rules already defined are reused :
SIMP_NOT_NOT : 
DISTRI_NOT_AND : 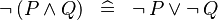
DISTRI_NOT_OR : 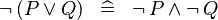
DERIV_NOT_IMP : 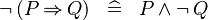
DERIV_NOT_FORALL : 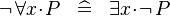
DERIV_NOT_EXISTS : 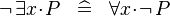
There is no rule implemented for that type of expression : 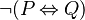 (which is equivalent to
(which is equivalent to 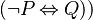 The way the reasoner will work is yet to be defined. Since the "
The way the reasoner will work is yet to be defined. Since the "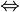 " is to be kept, the choice on which predicate the not will be applied to is ambiguous. Here is an example showing that difficulty :
" is to be kept, the choice on which predicate the not will be applied to is ambiguous. Here is an example showing that difficulty :
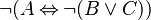 (1) which is equivalent to
(1) which is equivalent to 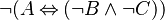 (2)
(2)
A solution would be to applied systematically on the left expression. In that case, simple simplification in the right member as in (1) would not be applied, thus complicating the left expression.
A better solution would to apply the  on a member containing already a
on a member containing already a  . But it can be hard to find an expression with a
. But it can be hard to find an expression with a  which has already been put in its Negation Normal Form as for the right member in (2)
which has already been put in its Negation Normal Form as for the right member in (2)
Implementation
Tactics
When an expression with a negation is matched, rules are applied following a prefix reading of that expression.
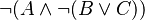
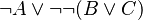
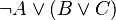
INSTEAD OF
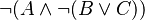
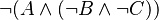
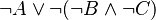
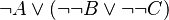
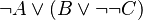
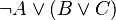
In that way, tree proof is not unnecessarily complicated, and so more legible. The space used on disk is also smaller.