Negation Normal Form

This page describe the Negation Normal Form used in Rodin and show how it has been implemented.

Definition

A logical formula is in its Negation Normal Form if negation occurs only on atomic expression. To achieve this, rules already defined are reused :

SIMP_NOT_NOT : $\lnot\, \lnot\, P \;\;\defi\;\; P$

DISTRI_NOT_AND : 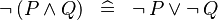$\lnot\,(P \land Q) \;\;\defi\;\; \lnot\, P \lor \lnot\, Q$

DISTRI_NOT_OR : 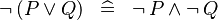$\lnot\,(P \lor Q) \;\;\defi\;\; \lnot\, P \land \lnot\, Q$

DERIV_NOT_IMP : 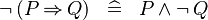$\lnot\,(P \limp Q) \;\;\defi\;\; P \land \lnot\, Q$

DERIV_NOT_FORALL : 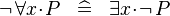$\lnot\, \forall x \qdot P \;\;\defi\;\; \exists x \qdot \lnot\, P$

DERIV_NOT_EXISTS : 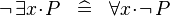$\lnot\, \exists x \qdot P \;\;\defi\;\; \forall x \qdot \lnot\, P$

There is no rule implemented for that type of expression : 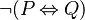$\lnot (P \leqv Q)$ (which is equivalent to 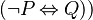$(\lnot P \leqv Q))$ The way the reasoner will work is yet to be defined. Since the "$\leqv$" is to be kept, the choice on which predicate the not will be applied to is ambiguous. Here is an example showing that difficulty :

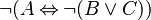$\lnot(A \leqv \lnot (B \lor C))$ (1) which is equivalent to 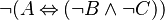$\lnot(A \leqv (\lnot B \land \lnot C))$ (2)

A solution would be to applied systematically on the left expression. In that case, simple simplification in the right member as in (1) would not be applied, thus complicating the left expression.

A better solution would to apply the $\lnot$ on a member containing already a $\lnot$. But it can be hard to find an expression with a $\lnot$ which has already been put in its Negation Normal Form as for the right member in (2)

Implementation

Tactics

When a predicate with a negation is matched, rules are applied following a pre-order traversal of that predicate.

$\lnot(A \land \lnot (B \lor C))$

$\lnot A \lor \lnot\lnot (B \lor C)$

$\lnot A \lor (B \lor C)$

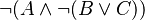
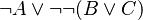
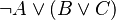
INSTEAD OF

$\lnot(A \land \lnot (B \lor C))$

$\lnot(A \land (\lnot B \land \lnot C))$

$\lnot A \lor \lnot(\lnot B \land \lnot C)$

$\lnot A \lor (\lnot\lnot B \lor \lnot\lnot C)$

$\lnot A \lor (B \lor \lnot\lnot C)$

$\lnot A \lor (B \lor C)$

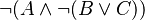
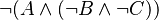
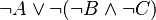
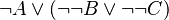
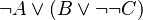
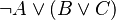
This way, tree proof is not unnecessarily complicated, and so more legible. The space used on disk is also smaller.