Proof Obligation Names (Rodin User Manual): Difference between revisions
imported>Mathieu m New page: Next is a table describing the names of context proof obligations: <center> {{SimpleHeader}} |Well-definedness of an Axiom||<math>m</math> / WD||<math>m</math> is the axiom name |- |Well... |
imported>Nicolas m Changed theorems for derived predicates |
||
| Line 5: | Line 5: | ||
|Well-definedness of an Axiom||<math>m</math> / WD||<math>m</math> is the axiom name | |Well-definedness of an Axiom||<math>m</math> / WD||<math>m</math> is the axiom name | ||
|- | |- | ||
|Well-definedness of a | |Well-definedness of a Derived Axiom||<math>m</math> / WD||<math>m</math> is the axiom name | ||
|- | |- | ||
| | |Derived Axiom||<math>m</math> / THM||<math>m</math> is the axiom name | ||
|} | |} | ||
</center> | </center> | ||
| Line 17: | Line 17: | ||
|Well-definedness of an Invariant||<math>v</math> / WD||<math>v</math> is the invariant name | |Well-definedness of an Invariant||<math>v</math> / WD||<math>v</math> is the invariant name | ||
|- | |- | ||
|Well-definedness of a | |Well-definedness of a Derived Invariant||<math>m</math> / WD||<math>m</math> is the invariant name | ||
|- | |- | ||
|Well-definedness of an event Guard||<math>t</math> / <math>d</math> / WD | |Well-definedness of an event Guard||<math>t</math> / <math>d</math> / WD | ||
| Line 34: | Line 34: | ||
<math>d</math> is the action name | <math>d</math> is the action name | ||
|- | |- | ||
| | |Derived Invariant||<math>m</math> / THM||<math>m</math> is the invariant name | ||
|- | |- | ||
|Invariant Establishment||INIT. / <math>v</math> / INV||<math>v</math> is the invariant name | |Invariant Establishment||INIT. / <math>v</math> / INV||<math>v</math> is the invariant name | ||
| Line 101: | Line 101: | ||
</center> | </center> | ||
Remark: At the moment, the deadlock freeness proof obligation generation is missing. If you need it, you can generate it yourself as a | Remark: At the moment, the deadlock freeness proof obligation generation is missing. If you need it, you can generate it yourself as a derived invariant saying the the disjunction of the abstract guards imply the disjunction of the concrete guards. | ||
Revision as of 16:28, 7 May 2009
Next is a table describing the names of context proof obligations:
| Well-definedness of an Axiom | 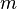 / WD / WD |
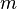 is the axiom name is the axiom name
|
| Well-definedness of a Derived Axiom | 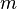 / WD / WD |
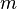 is the axiom name is the axiom name
|
| Derived Axiom | 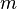 / THM / THM |
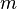 is the axiom name is the axiom name
|
Next is a table showing the name of machine proof obligations:
| Well-definedness of an Invariant | 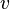 / WD / WD |
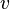 is the invariant name is the invariant name
|
| Well-definedness of a Derived Invariant | 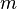 / WD / WD |
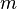 is the invariant name is the invariant name
|
| Well-definedness of an event Guard |  / / 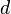 / WD / WD
|
 is the event name is the event name
|
| Well-definedness of an event Action |  / / 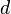 / WD / WD
|
 is the event name is the event name
|
| Feasibility of a non-det. event Action |  / / 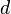 / FIS / FIS
|
 is the event name is the event name
|
| Derived Invariant | 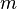 / THM / THM |
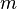 is the invariant name is the invariant name
|
| Invariant Establishment | INIT. / 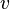 / INV / INV |
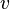 is the invariant name is the invariant name
|
| Invariant Preservation |  / / 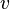 / INV / INV
|
 is the event name is the event name
|
Next are the proof obligations concerned with machine refinements:
| Guard Strengthening |  / / 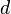 / GRD / GRD
|
 is the concrete event name is the concrete event name
|
| Guard Strengthening (merge) |  / MRG / MRG |
 is the concrete event name is the concrete event name
|
| Action Simulation |  / / 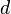 / SIM / SIM
|
 is the concrete event name is the concrete event name
|
| Equality of a preserved Variable |  / / 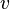 / EQL / EQL
|
 is the concrete event name is the concrete event name
|
Next are the proof obligations concerned with the new events variant:
| Well definedness of Variant | VWD | |
| Finiteness for a set Variant | FIN | |
| Natural number for a numeric Variant |  / NAT / NAT |
 is the new event name is the new event name
|
| Decreasing of Variant |  / VAR / VAR |
 is the new event name is the new event name
|
Finally, here are the proof obligations concerned with witnesses:
| Well definedness of Witness |  / / 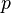 / WWD / WWD
|
 is the concrete event name is the concrete event name
or a primed variable name |
| Feasibility of non-det. Witness |  / / 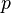 / WFIS / WFIS
|
 is the concrete event name is the concrete event name
or a primed variable name |
Remark: At the moment, the deadlock freeness proof obligation generation is missing. If you need it, you can generate it yourself as a derived invariant saying the the disjunction of the abstract guards imply the disjunction of the concrete guards.