Proof Skeleton View

Do not edit! This content has been migrated to Subversion.
(Nightly Handbook Build)

Purpose

The Proof Skeleton View allows to quickly browse through a proof built either automatically or interactively with the Rodin prover. This view can be used on any proof, independently of the presence of a corresponding proof obligation.

Furthermore, this view allows user to see together proof rules and corresponding sequents.

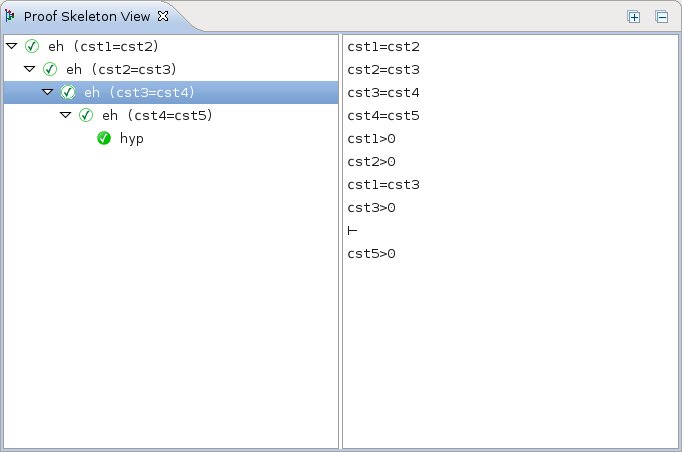
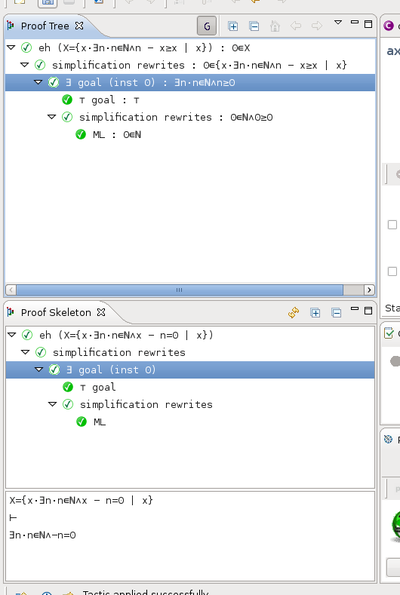
The Proof Skeleton View

Showing the View

The Proof Skeleton View is available as other views in the Window > Show View > Other > Event-B > Proof Skeleton View menu.

To watch a proof skeleton, simply select a proof obligation or a proof file in the Event-B Explorer.

View Interpretation

Proof skeletons are displayed in a two-part view. On the left-hand side is the tree structure of rules applied in the proof. On the right-hand side stands the sequent on which the currently selected rule is applied. The proof which is displayed is the one stored in the proof file on disk, never the one which is currently edited through the proof control. This can be very handy as it can allow one to see the previous proof of a proof obligation while working on a new proof of it.

The tree can be expanded or collapsed by using [+] and [-] buttons on the upper right corner.

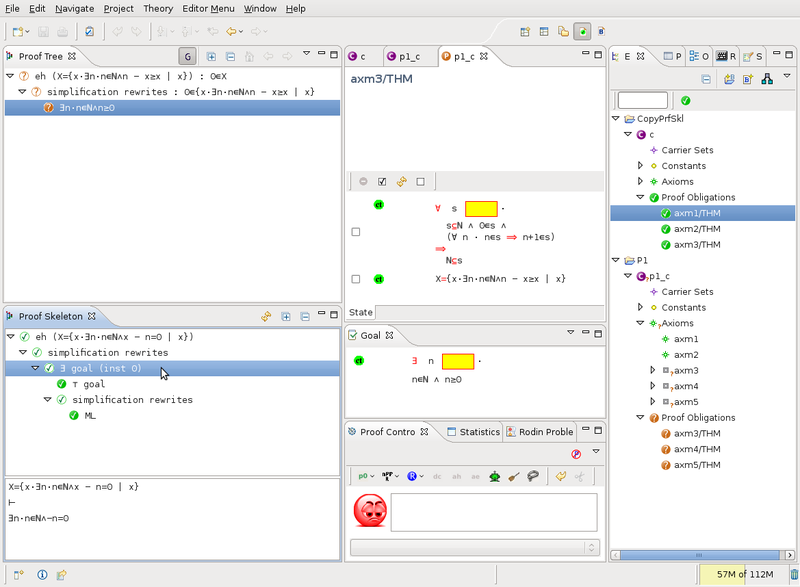
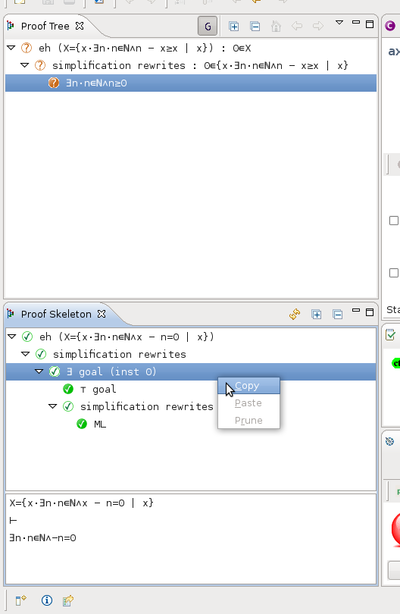
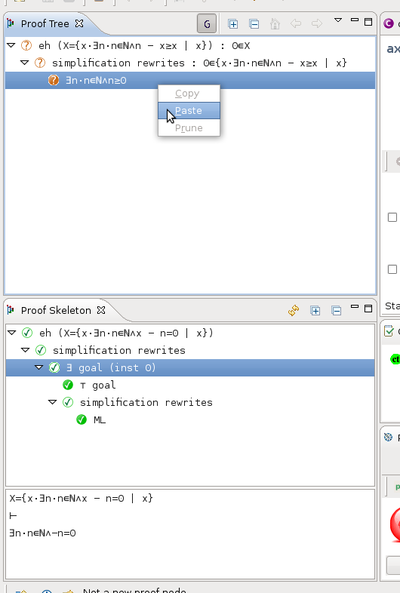
Copy/Paste to Proof Tree

The copy/paste feature allows to reuse a stored proof into a new proof. Starting from the following configuration:

where the proof we are working on (top left) is similar to another proof whose skeleton is displayed on bottom left. We can then copy/paste the interesting sub tree from the skeleton to the proof: