Relation Rewrite Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Laurent Fixed broken rules DISTRI_DOMSUB_BUNION_L, DISTRI_DOMSUB_BINTER_L, DISTRI_RANSUB_BUNION_R and DISTRI_RANSUB_BINTER_R |
imported>Tommy m removed * on unimplemented rules |
||
| Line 1: | Line 1: | ||
{{RRHeader}} | {{RRHeader}} | ||
{{RRRow}}|*||{{Rulename|SIMP_DOM_COMPSET}}||<math> \dom (\{ x \mapsto a, \ldots , y \mapsto b\} ) \;\;\defi\;\; \{ x, \ldots , y\} </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_DOM_COMPSET}}||<math> \dom (\{ x \mapsto a, \ldots , y \mapsto b\} ) \;\;\defi\;\; \{ x, \ldots , y\} </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOM_CONVERSE}}||<math> \dom (r^{-1} ) \;\;\defi\;\; \ran (r) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_RAN_COMPSET}}||<math> \ran (\{ x \mapsto a, \ldots , y \mapsto b\} ) \;\;\defi\;\; \{ a, \ldots , b\} </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_RAN_COMPSET}}||<math> \ran (\{ x \mapsto a, \ldots , y \mapsto b\} ) \;\;\defi\;\; \{ a, \ldots , b\} </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RAN_CONVERSE}}||<math> \ran (r^{-1} ) \;\;\defi\;\; \dom (r) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_OVERL}}||<math> r \ovl \ldots \ovl \emptyset \ovl \ldots \ovl s \;\;\defi\;\; r \ovl \ldots \ovl s </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_OVERL}}||<math> r \ovl \ldots \ovl \emptyset \ovl \ldots \ovl s \;\;\defi\;\; r \ovl \ldots \ovl s </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_MULTI_OVERL}}||<math>\begin{array}{cl} & r \ovl \cdots \ovl s \ovl t \ovl \cdots \ovl t \ovl \cdots \ovl u \\ \defi & r \ovl \cdots \ovl s \ovl \cdots \ovl t \ovl \cdots \ovl u \end{array}</math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_MULTI_OVERL}}||<math>\begin{array}{cl} & r \ovl \cdots \ovl s \ovl t \ovl \cdots \ovl t \ovl \cdots \ovl u \\ \defi & r \ovl \cdots \ovl s \ovl \cdots \ovl t \ovl \cdots \ovl u \end{array}</math>|| || A | ||
| Line 9: | Line 9: | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMRES_L}}||<math> \emptyset \domres r \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMRES_L}}||<math> \emptyset \domres r \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMRES_R}}||<math> S \domres \emptyset \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMRES_R}}||<math> S \domres \emptyset \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_DOMRES}}||<math> \mathit{Ty} \domres r \;\;\defi\;\; r </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_DOMRES_DOM}}||<math> \dom (r) \domres r \;\;\defi\;\; r </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_DOMRES_RAN}}||<math> \ran (r) \domres r^{-1} \;\;\defi\;\; r^{-1} </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOMRES_ID}}||<math> S \domres (T \domres \id) \;\;\defi\;\; (S \binter T) \domres \id </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANRES_R}}||<math> r \ranres \emptyset \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANRES_R}}||<math> r \ranres \emptyset \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANRES_L}}||<math> \emptyset \ranres S \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANRES_L}}||<math> \emptyset \ranres S \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_RANRES}}||<math> r \ranres \mathit{Ty} \;\;\defi\;\; r </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RANRES_RAN}}||<math> r \ranres \ran (r) \;\;\defi\;\; r </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RANRES_DOM}}||<math> r^{-1} \ranres \dom (r) \;\;\defi\;\; r^{-1} </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RANRES_ID}}||<math> (S \domres \id) \ranres T \;\;\defi\;\; (S \binter T) \domres \id </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMSUB_L}}||<math> \emptyset \domsub r \;\;\defi\;\; r </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMSUB_L}}||<math> \emptyset \domsub r \;\;\defi\;\; r </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMSUB_R}}||<math> S \domsub \emptyset \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DOMSUB_R}}||<math> S \domsub \emptyset \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_DOMSUB}}||<math> \mathit{Ty} \domsub r \;\;\defi\;\; \emptyset </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_DOMSUB_DOM}}||<math> \dom (r) \domsub r \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOMSUB_ID}}||<math> S \domsub (T \domres \id ) \;\;\defi\;\; (T \setminus S) \domres \id </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANSUB_R}}||<math> r \ransub \emptyset \;\;\defi\;\; r </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANSUB_R}}||<math> r \ransub \emptyset \;\;\defi\;\; r </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANSUB_L}}||<math> \emptyset \ransub S \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RANSUB_L}}||<math> \emptyset \ransub S \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_RANSUB}}||<math> r \ransub \mathit{Ty} \;\;\defi\;\; \emptyset </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RANSUB_RAN}}||<math> r \ransub \ran (r) \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RANSUB_ID}}||<math> (S \domres \id) \ransub T \;\;\defi\;\; (S \setminus T) \domres \id </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_FCOMP}}||<math> r \fcomp \ldots \fcomp \emptyset \fcomp \ldots \fcomp s \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_FCOMP}}||<math> r \fcomp \ldots \fcomp \emptyset \fcomp \ldots \fcomp s \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_FCOMP_ID}}||<math> r \fcomp \ldots \fcomp \id \fcomp \ldots \fcomp s \;\;\defi\;\; r \fcomp \ldots \fcomp s </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_FCOMP_R}}||<math> r \fcomp \mathit{Ty} \;\;\defi\;\; \dom (r) \cprod \mathit{Tb} </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \cprod \mathit{Tb}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_FCOMP_L}}||<math> \mathit{Ty} \fcomp r \;\;\defi\;\; \mathit{Ta} \cprod \ran (r) </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \cprod \mathit{Tb}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FCOMP_ID}}||<math> r \fcomp \ldots \fcomp S \domres \id \fcomp T \domres \id \fcomp \ldots s \;\;\defi\;\; r \fcomp \ldots \fcomp (S \binter T) \domres \id \fcomp \ldots \fcomp s </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_BCOMP}}||<math> r \bcomp \ldots \bcomp \emptyset \bcomp \ldots \bcomp s \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_BCOMP}}||<math> r \bcomp \ldots \bcomp \emptyset \bcomp \ldots \bcomp s \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_BCOMP_ID}}||<math> r \bcomp \ldots \bcomp \id \bcomp \ldots \bcomp s \;\;\defi\;\; r \bcomp \ldots \bcomp s </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_BCOMP_L}}||<math> \mathit{Ty} \bcomp r \;\;\defi\;\; \dom (r) \cprod \mathit{Tb} </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \cprod \mathit{Tb}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_BCOMP_R}}||<math> r \bcomp \mathit{Ty} \;\;\defi\;\; \mathit{Ta} \cprod \ran (r) </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \cprod \mathit{Tb}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_BCOMP_ID}}||<math> r \bcomp \ldots \bcomp S \domres \id \bcomp T \domres \id \bcomp \ldots \bcomp s \;\;\defi\;\; r \bcomp \ldots \bcomp (S \binter T) \domres \id \bcomp \ldots \bcomp s </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DPROD_R}}||<math> r \dprod \emptyset \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DPROD_R}}||<math> r \dprod \emptyset \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DPROD_L}}||<math> \emptyset \dprod r \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_DPROD_L}}||<math> \emptyset \dprod r \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_DPROD}}||<math> \mathit{Ta} \dprod \mathit{Tb} \;\;\defi\;\; Tc \cprod (Td \cprod Te) </math>|| where <math>\mathit{Ta}</math> and <math>\mathit{Tb}</math> are type expressions and <math>\mathit{Ta} = \mathit{Tc} \cprod \mathit{Td}</math> and <math>\mathit{Tb} = \mathit{Tc} \cprod \mathit{Te}</math> || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PPROD_R}}||<math> r \pprod \emptyset \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PPROD_R}}||<math> r \pprod \emptyset \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PPROD_L}}||<math> \emptyset \pprod r \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PPROD_L}}||<math> \emptyset \pprod r \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_PPROD}}||<math> \mathit{Ta} \pprod \mathit{Tb} \;\;\defi\;\; (Tc \cprod Te) \cprod (Td \cprod Tf) </math>|| where <math>\mathit{Ta}</math> and <math>\mathit{Tb}</math> are type expressions and <math>\mathit{Ta} = \mathit{Tc} \cprod \mathit{Td}</math> and <math>\mathit{Tb} = \mathit{Te} \cprod \mathit{Tf}</math> || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_RELIMAGE_R}}||<math> r[\emptyset ] \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_RELIMAGE_R}}||<math> r[\emptyset ] \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RELIMAGE_L}}||<math> \emptyset [S] \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_RELIMAGE_L}}||<math> \emptyset [S] \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_RELIMAGE}}||<math> r[Ty] \;\;\defi\;\; \ran (r) </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_RELIMAGE_DOM}}||<math> r[\dom (r)] \;\;\defi\;\; \ran (r) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_RELIMAGE_DOM}}||<math> r[\dom (r)] \;\;\defi\;\; \ran (r) </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_RELIMAGE_ID}}||<math> \id[T] \;\;\defi\;\; T </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RELIMAGE_ID}}||<math> (S \domres \id)[T] \;\;\defi\;\; S \binter T </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RELIMAGE_CPROD_SING}}||<math> (\{ E\} \cprod S)[\{ E\} ] \;\;\defi\;\; S </math>|| where <math>E</math> is a single expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RELIMAGE_SING_MAPSTO}}||<math> \{ E \mapsto F\} [\{ E\} ] \;\;\defi\;\; \{ F\} </math>|| where <math>E</math> is a single expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RELIMAGE_CONVERSE_RANSUB}}||<math> (r \ransub S)^{-1} [S] \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RELIMAGE_CONVERSE_RANRES}}||<math> (r \ranres S)^{-1} [S] \;\;\defi\;\; r^{-1} [S] </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RELIMAGE_CONVERSE_DOMSUB}}||<math> (S \domsub r)^{-1} [T] \;\;\defi\;\; r^{-1} [T] \setminus S </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DERIV_RELIMAGE_RANSUB}}||<math> (r \ransub S)[T] \;\;\defi\;\; r[T] \setminus S </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DERIV_RELIMAGE_RANRES}}||<math> (r \ranres S)[T] \;\;\defi\;\; r[T] \binter S </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RELIMAGE_DOMSUB}}||<math> (S \domsub r)[S] \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DERIV_RELIMAGE_DOMSUB}}||<math> (S \domsub r)[T] \;\;\defi\;\; r[T \setminus S] </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DERIV_RELIMAGE_DOMRES}}||<math> (S \domres r)[T] \;\;\defi\;\; r[S \binter T] </math>|| || M | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_CONVERSE}}||<math> \emptyset ^{-1} \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_CONVERSE}}||<math> \emptyset ^{-1} \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_CONVERSE_ID}}||<math> \id^{-1} \;\;\defi\;\; \id </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_CONVERSE}}||<math> \mathit{Ty}^{-1} \;\;\defi\;\; \mathit{Tb} \cprod \mathit{Ta} </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \cprod \mathit{Tb}</math> || A | ||
{{RRRow}}|*||{{Rulename|SIMP_CONVERSE_SETENUM}}||<math> \{ x \mapsto a, \ldots , y \mapsto b\} ^{-1} \;\;\defi\;\; \{ a \mapsto x, \ldots , b \mapsto y\} </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_CONVERSE_SETENUM}}||<math> \{ x \mapsto a, \ldots , y \mapsto b\} ^{-1} \;\;\defi\;\; \{ a \mapsto x, \ldots , b \mapsto y\} </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_CONVERSE_COMPSET}}||<math> \{ X \qdot P \mid x\mapsto y\} ^{-1} \;\;\defi\;\; \{ X \qdot P \mid y\mapsto x\} </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_CONVERSE_COMPSET}}||<math> \{ X \qdot P \mid x\mapsto y\} ^{-1} \;\;\defi\;\; \{ X \qdot P \mid y\mapsto x\} </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_ID}}||<math> \emptyset \domres \id \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_ID}}||<math> \emptyset \domres \id \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOM_ID}}||<math> \dom (\id) \;\;\defi\;\; S </math>|| where <math>\id</math> has type <math>\pow(S \cprod S)</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RAN_ID}}||<math> \ran (\id) \;\;\defi\;\; S </math>|| where <math>\id</math> has type <math>\pow(S \cprod S)</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FCOMP_ID_L}}||<math> (S \domres \id) \fcomp r \;\;\defi\;\; S \domres r </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FCOMP_ID_R}}||<math> r \fcomp (S \domres \id) \;\;\defi\;\; r \ranres S </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_REL_R}}||<math> S \rel \emptyset \;\;\defi\;\; \{ \emptyset \} </math>|| idem for operators <math>\srel \pfun \pinj \psur</math> || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_REL_R}}||<math> S \rel \emptyset \;\;\defi\;\; \{ \emptyset \} </math>|| idem for operators <math>\srel \pfun \pinj \psur</math> || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_REL_L}}||<math> \emptyset \rel S \;\;\defi\;\; \{ \emptyset \} </math>|| idem for operators <math>\trel \pfun \tfun \pinj \tinj</math> || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_REL_L}}||<math> \emptyset \rel S \;\;\defi\;\; \{ \emptyset \} </math>|| idem for operators <math>\trel \pfun \tfun \pinj \tinj</math> || A | ||
| Line 77: | Line 77: | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PRJ1}}||<math> \emptyset \domres \prjone \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PRJ1}}||<math> \emptyset \domres \prjone \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PRJ2}}||<math> \emptyset \domres \prjtwo \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_PRJ2}}||<math> \emptyset \domres \prjtwo \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FUNIMAGE_PRJ1}}||<math> \prjone (E \mapsto F) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FUNIMAGE_PRJ2}}||<math> \prjtwo (E \mapsto F) \;\;\defi\;\; F </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOM_PRJ1}}||<math> \dom (\prjone) \;\;\defi\;\; S \cprod T </math>|| where <math>\prjone</math> has type <math>\pow(S \cprod T \cprod S)</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOM_PRJ2}}||<math> \dom (\prjtwo) \;\;\defi\;\; S \cprod T </math>|| where <math>\prjtwo</math> has type <math>\pow(S \cprod T \cprod T)</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RAN_PRJ1}}||<math> \ran (\prjone) \;\;\defi\;\; S </math>|| where <math>\prjone</math> has type <math>\pow(S \cprod T \cprod S)</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RAN_PRJ2}}||<math> \ran (\prjtwo) \;\;\defi\;\; T </math>|| where <math>\prjtwo</math> has type <math>\pow(S \cprod T \cprod T)</math> || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_LAMBDA}}||<math> (\lambda x \qdot \bfalse \mid E) \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_LAMBDA}}||<math> (\lambda x \qdot \bfalse \mid E) \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FUNIMAGE_LAMBDA}}||<math> (\lambda x \qdot P(x) \mid E(x))(y) \;\;\defi\;\; E(y) </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_DOM_LAMBDA}}||<math> \dom (\lambda x \qdot P \mid E) \;\;\defi\;\; \{ x\qdot P \mid x\} </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_RAN_LAMBDA}}||<math> \ran (\lambda x \qdot P \mid E) \;\;\defi\;\; \{ x\qdot P \mid E\} </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_FUNIMAGE_SETENUM_LL}}||<math> \{ A \mapsto E, \ldots , B \mapsto E\} (x) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_FUNIMAGE_SETENUM_LR}}||<math> \{ A \mapsto E, \ldots , x \mapsto y, \ldots , B \mapsto F\} (x) \;\;\defi\;\; y </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_FUNIMAGE_OVERL_SETENUM}}||<math> (r \ovl \ldots \ovl \{ A \mapsto E, \ldots , x \mapsto y, \ldots , B \mapsto F\} )(x) \;\;\defi\;\; y </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_FUNIMAGE_OVERL_SETENUM}}||<math> (r \ovl \ldots \ovl \{ A \mapsto E, \ldots , x \mapsto y, \ldots , B \mapsto F\} )(x) \;\;\defi\;\; y </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_FUNIMAGE_BUNION_SETENUM}}||<math> (r \bunion \ldots \bunion \{ A \mapsto E, \ldots , x \mapsto y, \ldots , B \mapsto F\} )(x) \;\;\defi\;\; y </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FUNIMAGE_CPROD}}||<math> (S \cprod \{ F\} )(x) \;\;\defi\;\; F </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FUNIMAGE_CPROD}}||<math> (S \cprod \{ F\} )(x) \;\;\defi\;\; F </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FUNIMAGE_ID}}||<math> \id (x) \;\;\defi\;\; x </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FUNIMAGE_FUNIMAGE_CONVERSE}}||<math> f(f^{-1} (E)) \;\;\defi\;\; E </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FUNIMAGE_FUNIMAGE_CONVERSE}}||<math> f(f^{-1} (E)) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FUNIMAGE_CONVERSE_FUNIMAGE}}||<math> f^{-1}(f(E)) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FUNIMAGE_FUNIMAGE_CONVERSE_SETENUM}}||<math> \{x \mapsto a, \ldots, y \mapsto b\}(\{a \mapsto x, \ldots, b \mapsto y\}(E)) \;\;\defi\;\; E </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FUNIMAGE_FUNIMAGE_CONVERSE_SETENUM}}||<math> \{x \mapsto a, \ldots, y \mapsto b\}(\{a \mapsto x, \ldots, b \mapsto y\}(E)) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DEF_BCOMP}}||<math> r \bcomp \ldots \bcomp s \;\;\defi\;\; s \fcomp \ldots \fcomp r </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DERIV_ID_SING}}||<math> \{ E\} \domres \id \;\;\defi\;\; \{ E \mapsto E\} </math>|| where <math>E</math> is a single expression || M | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_DOM}}||<math> \dom (\emptyset ) \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_DOM}}||<math> \dom (\emptyset ) \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_RAN}}||<math> \ran (\emptyset ) \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_RAN}}||<math> \ran (\emptyset ) \;\;\defi\;\; \emptyset </math>|| || A | ||
| Line 107: | Line 107: | ||
{{RRRow}}|*||{{Rulename|DERIV_FCOMP_RANSUB}}||<math> p \fcomp (q \ransub s) \;\;\defi\;\; (p \fcomp q) \ransub s </math>|| || M | {{RRRow}}|*||{{Rulename|DERIV_FCOMP_RANSUB}}||<math> p \fcomp (q \ransub s) \;\;\defi\;\; (p \fcomp q) \ransub s </math>|| || M | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_EQUAL_RELDOMRAN}}||<math> \emptyset \strel \emptyset \;\;\defi\;\; \{ \emptyset \} </math>|| idem for operators <math>\tsur \tbij</math> || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_EQUAL_RELDOMRAN}}||<math> \emptyset \strel \emptyset \;\;\defi\;\; \{ \emptyset \} </math>|| idem for operators <math>\tsur \tbij</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_DOM}}||<math> \dom (\mathit{Ty}) \;\;\defi\;\; \mathit{Ta} </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \rel \mathit{Tb}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_RAN}}||<math> \ran (\mathit{Ty}) \;\;\defi\;\; \mathit{Tb} </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \rel \mathit{Tb}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_DOM_CPROD}}||<math> \dom (E \cprod E) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_RAN_CPROD}}||<math> \ran (E \cprod E) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}|*||{{Rulename|DEF_IN_DOM}}||<math> E \in \dom (r) \;\;\defi\;\; \exists y \qdot E \mapsto y \in r </math>|| || M | {{RRRow}}|*||{{Rulename|DEF_IN_DOM}}||<math> E \in \dom (r) \;\;\defi\;\; \exists y \qdot E \mapsto y \in r </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DEF_IN_RAN}}||<math> F \in \ran (r) \;\;\defi\;\; \exists x \qdot x \mapsto F \in r </math>|| || M | {{RRRow}}|*||{{Rulename|DEF_IN_RAN}}||<math> F \in \ran (r) \;\;\defi\;\; \exists x \qdot x \mapsto F \in r </math>|| || M | ||
| Line 138: | Line 138: | ||
{{RRRow}}|*||{{Rulename|DISTRI_FCOMP_BUNION_R}}||<math> p \fcomp (q \bunion r) \;\;\defi\;\; (p \fcomp q) \bunion (p \fcomp r) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_FCOMP_BUNION_R}}||<math> p \fcomp (q \bunion r) \;\;\defi\;\; (p \fcomp q) \bunion (p \fcomp r) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_FCOMP_BUNION_L}}||<math> (q \bunion r) \fcomp p \;\;\defi\;\; (q \fcomp p) \bunion (r \fcomp p) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_FCOMP_BUNION_L}}||<math> (q \bunion r) \fcomp p \;\;\defi\;\; (q \fcomp p) \bunion (r \fcomp p) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DPROD_BUNION}}||<math> r \dprod (s \bunion t) \;\;\defi\;\; (r \dprod s) \bunion (r \dprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DPROD_BINTER}}||<math> r \dprod (s \binter t) \;\;\defi\;\; (r \dprod s) \binter (r \dprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DPROD_SETMINUS}}||<math> r \dprod (s \setminus t) \;\;\defi\;\; (r \dprod s) \setminus (r \dprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DPROD_OVERL}}||<math> r \dprod (s \ovl t) \;\;\defi\;\; (r \dprod s) \ovl (r \dprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_PPROD_BUNION}}||<math> r \pprod (s \bunion t) \;\;\defi\;\; (r \pprod s) \bunion (r \pprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_PPROD_BINTER}}||<math> r \pprod (s \binter t) \;\;\defi\;\; (r \pprod s) \binter (r \pprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_PPROD_SETMINUS}}||<math> r \pprod (s \setminus t) \;\;\defi\;\; (r \pprod s) \setminus (r \pprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_PPROD_OVERL}}||<math> r \pprod (s \ovl t) \;\;\defi\;\; (r \pprod s) \ovl (r \pprod t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_OVERL_BUNION_L}}||<math> (p \bunion q) \ovl r \;\;\defi\;\; (p \ovl r) \bunion (q \ovl r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_OVERL_BINTER_L}}||<math> (p \binter q) \ovl r \;\;\defi\;\; (p \ovl r) \binter (q \ovl r) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BUNION_R}}||<math> s \domres (p \bunion q) \;\;\defi\;\; (s \domres p) \bunion (s \domres q) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BUNION_R}}||<math> s \domres (p \bunion q) \;\;\defi\;\; (s \domres p) \bunion (s \domres q) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BUNION_L}}||<math> (s \bunion t) \domres r \;\;\defi\;\; (s \domres r) \bunion (t \domres r) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BUNION_L}}||<math> (s \bunion t) \domres r \;\;\defi\;\; (s \domres r) \bunion (t \domres r) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BINTER_R}}||<math> s \domres (p \binter q) \;\;\defi\;\; (s \domres p) \binter (s \domres q) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BINTER_R}}||<math> s \domres (p \binter q) \;\;\defi\;\; (s \domres p) \binter (s \domres q) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BINTER_L}}||<math> (s \binter t) \domres r \;\;\defi\;\; (s \domres r) \binter (t \domres r) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOMRES_BINTER_L}}||<math> (s \binter t) \domres r \;\;\defi\;\; (s \domres r) \binter (t \domres r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DOMRES_SETMINUS_R}}||<math> s \domres (p \setminus q) \;\;\defi\;\; (s \domres p) \setminus (s \domres q) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DOMRES_SETMINUS_L}}||<math> (s \setminus t) \domres r \;\;\defi\;\; (s \domres r) \setminus (t \domres r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DOMRES_DPROD}}||<math> s \domres (p \dprod q) \;\;\defi\;\; (s \domres p) \dprod (s \domres q) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DOMRES_OVERL}}||<math> s \domres (r \ovl q) \;\;\defi\;\; (s \domres r) \ovl (s \domres q) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOMSUB_BUNION_R}}||<math> s \domsub (p \bunion q) \;\;\defi\;\; (s \domsub p) \bunion (s \domsub q) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOMSUB_BUNION_R}}||<math> s \domsub (p \bunion q) \;\;\defi\;\; (s \domsub p) \bunion (s \domsub q) </math>|| || M | ||
{{RRRow}}|b||{{Rulename|DISTRI_DOMSUB_BUNION_L}}||<math> (s \bunion t) \domsub r \;\;\defi\;\; (s \domsub r) \binter (t \domsub r) </math>|| || M | {{RRRow}}|b||{{Rulename|DISTRI_DOMSUB_BUNION_L}}||<math> (s \bunion t) \domsub r \;\;\defi\;\; (s \domsub r) \binter (t \domsub r) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOMSUB_BINTER_R}}||<math> s \domsub (p \binter q) \;\;\defi\;\; (s \domsub p) \binter (s \domsub q) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOMSUB_BINTER_R}}||<math> s \domsub (p \binter q) \;\;\defi\;\; (s \domsub p) \binter (s \domsub q) </math>|| || M | ||
{{RRRow}}|b||{{Rulename|DISTRI_DOMSUB_BINTER_L}}||<math> (s \binter t) \domsub r \;\;\defi\;\; (s \domsub r) \bunion (t \domsub r) </math>|| || M | {{RRRow}}|b||{{Rulename|DISTRI_DOMSUB_BINTER_L}}||<math> (s \binter t) \domsub r \;\;\defi\;\; (s \domsub r) \bunion (t \domsub r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DOMSUB_DPROD}}||<math> A \domsub (r \dprod s) \;\;\defi\;\; (A \domsub r) \dprod (A \domsub s) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_DOMSUB_OVERL}}||<math> A \domsub (r \ovl s) \;\;\defi\;\; (A \domsub r) \ovl (A \domsub s) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_RANRES_BUNION_R}}||<math> r \ranres (s \bunion t) \;\;\defi\;\; (r \ranres s) \bunion (r \ranres t) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RANRES_BUNION_R}}||<math> r \ranres (s \bunion t) \;\;\defi\;\; (r \ranres s) \bunion (r \ranres t) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_RANRES_BUNION_L}}||<math> (p \bunion q) \ranres s \;\;\defi\;\; (p \ranres s) \bunion (q \ranres s) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RANRES_BUNION_L}}||<math> (p \bunion q) \ranres s \;\;\defi\;\; (p \ranres s) \bunion (q \ranres s) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_RANRES_BINTER_R}}||<math> r \ranres (s \binter t) \;\;\defi\;\; (r \ranres s) \binter (r \ranres t) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RANRES_BINTER_R}}||<math> r \ranres (s \binter t) \;\;\defi\;\; (r \ranres s) \binter (r \ranres t) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_RANRES_BINTER_L}}||<math> (p \binter q) \ranres s \;\;\defi\;\; (p \ranres s) \binter (q \ranres s) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RANRES_BINTER_L}}||<math> (p \binter q) \ranres s \;\;\defi\;\; (p \ranres s) \binter (q \ranres s) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_RANRES_SETMINUS_R}}||<math> r \ranres (s \setminus t) \;\;\defi\;\; (r \ranres s) \setminus (r \ranres t) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_RANRES_SETMINUS_L}}||<math> (p \setminus q) \ranres s \;\;\defi\;\; (p \ranres s) \setminus (q \ranres s) </math>|| || M | ||
{{RRRow}}|b||{{Rulename|DISTRI_RANSUB_BUNION_R}}||<math> r \ransub (s\bunion t) \;\;\defi\;\; (r \ransub s) \binter (r \ransub t) </math>|| || M | {{RRRow}}|b||{{Rulename|DISTRI_RANSUB_BUNION_R}}||<math> r \ransub (s\bunion t) \;\;\defi\;\; (r \ransub s) \binter (r \ransub t) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_RANSUB_BUNION_L}}||<math> (p \bunion q) \ransub s \;\;\defi\;\; (p \ransub s) \bunion (q \ransub s) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RANSUB_BUNION_L}}||<math> (p \bunion q) \ransub s \;\;\defi\;\; (p \ransub s) \bunion (q \ransub s) </math>|| || M | ||
| Line 173: | Line 173: | ||
{{RRRow}}|*||{{Rulename|DISTRI_RANSUB_BINTER_L}}||<math> (p \binter q) \ransub s \;\;\defi\;\; (p \ransub s) \binter (q \ransub s) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RANSUB_BINTER_L}}||<math> (p \binter q) \ransub s \;\;\defi\;\; (p \ransub s) \binter (q \ransub s) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_CONVERSE_BUNION}}||<math> (p \bunion q)^{-1} \;\;\defi\;\; p^{-1} \bunion q^{-1} </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_CONVERSE_BUNION}}||<math> (p \bunion q)^{-1} \;\;\defi\;\; p^{-1} \bunion q^{-1} </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_BINTER}}||<math> (p \binter q)^{-1} \;\;\defi\;\; p^{-1} \binter q^{-1} </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_SETMINUS}}||<math> (r \setminus s)^{-1} \;\;\defi\;\; r^{-1} \setminus s^{-1} </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_BCOMP}}||<math> (r \bcomp s)^{-1} \;\;\defi\;\; (s^{-1} \bcomp r^{-1} ) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_FCOMP}}||<math> (p \fcomp q)^{-1} \;\;\defi\;\; (q^{-1} \fcomp p^{-1} ) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_PPROD}}||<math> (r \pprod s)^{-1} \;\;\defi\;\; r^{-1} \pprod s^{-1} </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_DOMRES}}||<math> (s \domres r)^{-1} \;\;\defi\;\; r^{-1} \ranres s </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_DOMSUB}}||<math> (s \domsub r)^{-1} \;\;\defi\;\; r^{-1} \ransub s </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_RANRES}}||<math> (r \ranres s)^{-1} \;\;\defi\;\; s \domres r^{-1} </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CONVERSE_RANSUB}}||<math> (r \ransub s)^{-1} \;\;\defi\;\; s \domsub r^{-1} </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_DOM_BUNION}}||<math> \dom (r \bunion s) \;\;\defi\;\; \dom (r) \bunion \dom (s) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_DOM_BUNION}}||<math> \dom (r \bunion s) \;\;\defi\;\; \dom (r) \bunion \dom (s) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_RAN_BUNION}}||<math> \ran (r \bunion s) \;\;\defi\;\; \ran (r) \bunion \ran (s) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_RAN_BUNION}}||<math> \ran (r \bunion s) \;\;\defi\;\; \ran (r) \bunion \ran (s) </math>|| || M | ||
Revision as of 10:45, 21 December 2009
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_DOM_COMPSET |
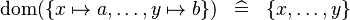 |
A | |
SIMP_DOM_CONVERSE |
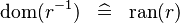 |
A | ||
| * | SIMP_RAN_COMPSET |
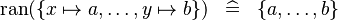 |
A | |
SIMP_RAN_CONVERSE |
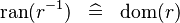 |
A | ||
| * | SIMP_SPECIAL_OVERL |
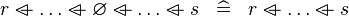 |
A | |
SIMP_MULTI_OVERL |
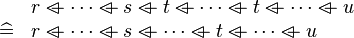 |
A | ||
| * | SIMP_TYPE_OVERL_CPROD |
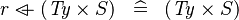 |
where  is a type expression is a type expression |
A |
SIMP_SPECIAL_DOMRES_L |
 |
A | ||
SIMP_SPECIAL_DOMRES_R |
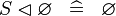 |
A | ||
SIMP_TYPE_DOMRES |
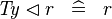 |
where  is a type expression is a type expression |
A | |
SIMP_MULTI_DOMRES_DOM |
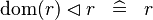 |
A | ||
SIMP_MULTI_DOMRES_RAN |
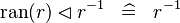 |
A | ||
SIMP_DOMRES_ID |
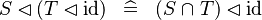 |
A | ||
SIMP_SPECIAL_RANRES_R |
 |
A | ||
SIMP_SPECIAL_RANRES_L |
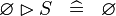 |
A | ||
SIMP_TYPE_RANRES |
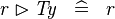 |
where  is a type expression is a type expression |
A | |
SIMP_MULTI_RANRES_RAN |
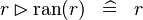 |
A | ||
SIMP_MULTI_RANRES_DOM |
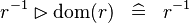 |
A | ||
SIMP_RANRES_ID |
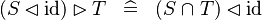 |
A | ||
SIMP_SPECIAL_DOMSUB_L |
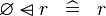 |
A | ||
SIMP_SPECIAL_DOMSUB_R |
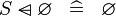 |
A | ||
SIMP_TYPE_DOMSUB |
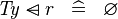 |
where  is a type expression is a type expression |
A | |
SIMP_MULTI_DOMSUB_DOM |
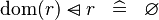 |
A | ||
SIMP_DOMSUB_ID |
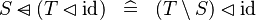 |
A | ||
SIMP_SPECIAL_RANSUB_R |
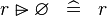 |
A | ||
SIMP_SPECIAL_RANSUB_L |
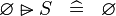 |
A | ||
SIMP_TYPE_RANSUB |
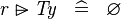 |
where  is a type expression is a type expression |
A | |
SIMP_MULTI_RANSUB_RAN |
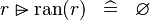 |
A | ||
SIMP_RANSUB_ID |
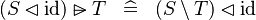 |
A | ||
SIMP_SPECIAL_FCOMP |
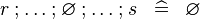 |
A | ||
SIMP_TYPE_FCOMP_ID |
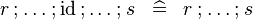 |
A | ||
SIMP_TYPE_FCOMP_R |
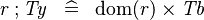 |
where  is a type expression equal to is a type expression equal to 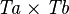 |
A | |
SIMP_TYPE_FCOMP_L |
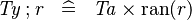 |
where  is a type expression equal to is a type expression equal to 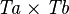 |
A | |
SIMP_FCOMP_ID |
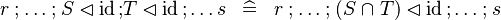 |
A | ||
SIMP_SPECIAL_BCOMP |
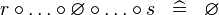 |
A | ||
SIMP_TYPE_BCOMP_ID |
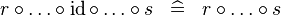 |
A | ||
SIMP_TYPE_BCOMP_L |
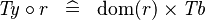 |
where  is a type expression equal to is a type expression equal to 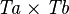 |
A | |
SIMP_TYPE_BCOMP_R |
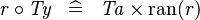 |
where  is a type expression equal to is a type expression equal to 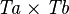 |
A | |
SIMP_BCOMP_ID |
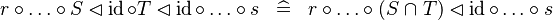 |
A | ||
SIMP_SPECIAL_DPROD_R |
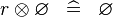 |
A | ||
SIMP_SPECIAL_DPROD_L |
 |
A | ||
SIMP_TYPE_DPROD |
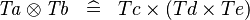 |
where 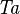 and and 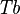 are type expressions and are type expressions and 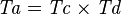 and and 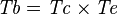 |
A | |
SIMP_SPECIAL_PPROD_R |
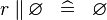 |
A | ||
SIMP_SPECIAL_PPROD_L |
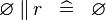 |
A | ||
SIMP_TYPE_PPROD |
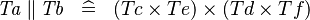 |
where 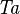 and and 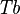 are type expressions and are type expressions and 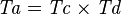 and and 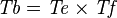 |
A | |
| * | SIMP_SPECIAL_RELIMAGE_R |
![r[\emptyset ] \;\;\defi\;\; \emptyset](/images/math/b/9/a/b9aaf14a5527d53ff1febab3e8883f03.png) |
A | |
SIMP_SPECIAL_RELIMAGE_L |
![\emptyset [S] \;\;\defi\;\; \emptyset](/images/math/6/4/8/648fbd380df0ae4c5d64da8bef51ee2d.png) |
A | ||
SIMP_TYPE_RELIMAGE |
![r[Ty] \;\;\defi\;\; \ran (r)](/images/math/0/2/1/02153b3e9f952be7157a4d4e336374a7.png) |
where  is a type expression is a type expression |
A | |
| * | SIMP_MULTI_RELIMAGE_DOM |
![r[\dom (r)] \;\;\defi\;\; \ran (r)](/images/math/0/3/4/0346b1b9c1146a8343fa2d18e1732769.png) |
A | |
SIMP_TYPE_RELIMAGE_ID |
![\id[T] \;\;\defi\;\; T](/images/math/4/0/0/4009c72979487233368b217afa41d8ad.png) |
A | ||
SIMP_RELIMAGE_ID |
![(S \domres \id)[T] \;\;\defi\;\; S \binter T](/images/math/b/e/2/be2ea9770f745da9730119cc0e6c7be3.png) |
A | ||
SIMP_MULTI_RELIMAGE_CPROD_SING |
![(\{ E\} \cprod S)[\{ E\} ] \;\;\defi\;\; S](/images/math/c/5/2/c526fc7db223ce0bfe920622d54d64e0.png) |
where  is a single expression is a single expression |
A | |
SIMP_MULTI_RELIMAGE_SING_MAPSTO |
![\{ E \mapsto F\} [\{ E\} ] \;\;\defi\;\; \{ F\}](/images/math/e/2/c/e2c3111e1660139c0d07f75c30de0e5c.png) |
where  is a single expression is a single expression |
A | |
SIMP_MULTI_RELIMAGE_CONVERSE_RANSUB |
![(r \ransub S)^{-1} [S] \;\;\defi\;\; \emptyset](/images/math/0/d/8/0d87a3a40feb382450061c80f9ed103e.png) |
A | ||
SIMP_MULTI_RELIMAGE_CONVERSE_RANRES |
![(r \ranres S)^{-1} [S] \;\;\defi\;\; r^{-1} [S]](/images/math/1/7/4/174952bb78d6d7afd42ee6a53ed2ac78.png) |
A | ||
SIMP_RELIMAGE_CONVERSE_DOMSUB |
![(S \domsub r)^{-1} [T] \;\;\defi\;\; r^{-1} [T] \setminus S](/images/math/3/4/2/342512ec589776fd0aae93fe8eb732e6.png) |
A | ||
DERIV_RELIMAGE_RANSUB |
![(r \ransub S)[T] \;\;\defi\;\; r[T] \setminus S](/images/math/5/9/3/5933212d9aad4f59b7641ea383b31a91.png) |
M | ||
DERIV_RELIMAGE_RANRES |
![(r \ranres S)[T] \;\;\defi\;\; r[T] \binter S](/images/math/1/9/9/1994ec5d3fa539db498124fe8fd4a27d.png) |
M | ||
SIMP_MULTI_RELIMAGE_DOMSUB |
![(S \domsub r)[S] \;\;\defi\;\; \emptyset](/images/math/b/f/3/bf31fb9e2da1545464bd5baecc397c01.png) |
A | ||
DERIV_RELIMAGE_DOMSUB |
![(S \domsub r)[T] \;\;\defi\;\; r[T \setminus S]](/images/math/f/2/4/f2407e5c136829c08c1bc390d74a77fe.png) |
M | ||
DERIV_RELIMAGE_DOMRES |
![(S \domres r)[T] \;\;\defi\;\; r[S \binter T]](/images/math/8/4/0/840633e87abc3f54638ede200920f377.png) |
M | ||
SIMP_SPECIAL_CONVERSE |
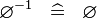 |
A | ||
SIMP_CONVERSE_ID |
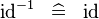 |
A | ||
SIMP_TYPE_CONVERSE |
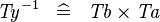 |
where  is a type expression equal to is a type expression equal to 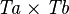 |
A | |
| * | SIMP_CONVERSE_SETENUM |
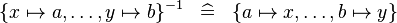 |
A | |
SIMP_CONVERSE_COMPSET |
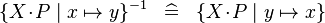 |
A | ||
SIMP_SPECIAL_ID |
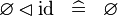 |
A | ||
SIMP_DOM_ID |
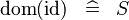 |
where 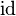 has type has type 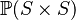 |
A | |
SIMP_RAN_ID |
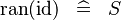 |
where 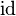 has type has type 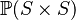 |
A | |
SIMP_FCOMP_ID_L |
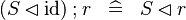 |
A | ||
SIMP_FCOMP_ID_R |
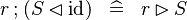 |
A | ||
SIMP_SPECIAL_REL_R |
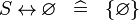 |
idem for operators 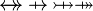 |
A | |
SIMP_SPECIAL_REL_L |
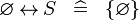 |
idem for operators 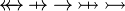 |
A | |
SIMP_SPECIAL_EQUAL_REL |
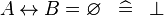 |
idem for operators 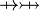 |
A | |
SIMP_SPECIAL_EQUAL_RELDOM |
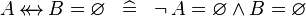 |
idem for operators 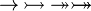 |
A | |
SIMP_SPECIAL_PRJ1 |
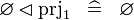 |
A | ||
SIMP_SPECIAL_PRJ2 |
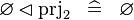 |
A | ||
SIMP_FUNIMAGE_PRJ1 |
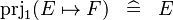 |
A | ||
SIMP_FUNIMAGE_PRJ2 |
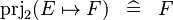 |
A | ||
SIMP_DOM_PRJ1 |
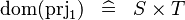 |
where 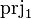 has type has type 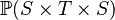 |
A | |
SIMP_DOM_PRJ2 |
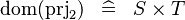 |
where 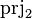 has type has type 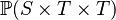 |
A | |
SIMP_RAN_PRJ1 |
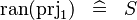 |
where 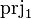 has type has type 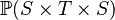 |
A | |
SIMP_RAN_PRJ2 |
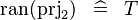 |
where 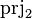 has type has type 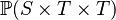 |
A | |
SIMP_SPECIAL_LAMBDA |
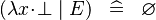 |
A | ||
SIMP_FUNIMAGE_LAMBDA |
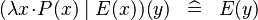 |
A | ||
SIMP_DOM_LAMBDA |
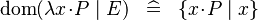 |
A | ||
SIMP_RAN_LAMBDA |
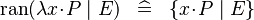 |
A | ||
SIMP_MULTI_FUNIMAGE_SETENUM_LL |
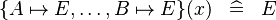 |
A | ||
SIMP_MULTI_FUNIMAGE_SETENUM_LR |
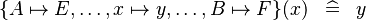 |
A | ||
| * | SIMP_MULTI_FUNIMAGE_OVERL_SETENUM |
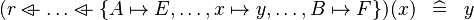 |
A | |
SIMP_MULTI_FUNIMAGE_BUNION_SETENUM |
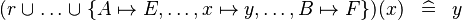 |
A | ||
| * | SIMP_FUNIMAGE_CPROD |
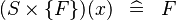 |
A | |
SIMP_FUNIMAGE_ID |
 |
A | ||
| * | SIMP_FUNIMAGE_FUNIMAGE_CONVERSE |
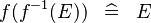 |
A | |
SIMP_FUNIMAGE_CONVERSE_FUNIMAGE |
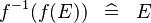 |
A | ||
| * | SIMP_FUNIMAGE_FUNIMAGE_CONVERSE_SETENUM |
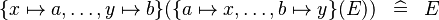 |
A | |
DEF_BCOMP |
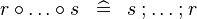 |
M | ||
DERIV_ID_SING |
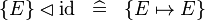 |
where  is a single expression is a single expression |
M | |
| * | SIMP_SPECIAL_DOM |
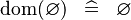 |
A | |
| * | SIMP_SPECIAL_RAN |
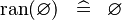 |
A | |
| * | SIMP_CONVERSE_CONVERSE |
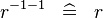 |
A | |
| * | DERIV_RELIMAGE_FCOMP |
![(p \fcomp q)[s] \;\;\defi\;\; q[p[s]]](/images/math/d/5/2/d525cb240947f85af66b077f0894364c.png) |
M | |
| * | DERIV_FCOMP_DOMRES |
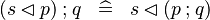 |
M | |
| * | DERIV_FCOMP_DOMSUB |
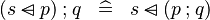 |
M | |
| * | DERIV_FCOMP_RANRES |
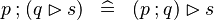 |
M | |
| * | DERIV_FCOMP_RANSUB |
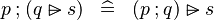 |
M | |
SIMP_SPECIAL_EQUAL_RELDOMRAN |
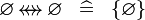 |
idem for operators 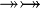 |
A | |
SIMP_TYPE_DOM |
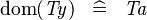 |
where  is a type expression equal to is a type expression equal to 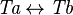 |
A | |
SIMP_TYPE_RAN |
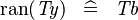 |
where  is a type expression equal to is a type expression equal to 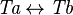 |
A | |
SIMP_MULTI_DOM_CPROD |
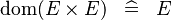 |
A | ||
SIMP_MULTI_RAN_CPROD |
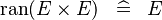 |
A | ||
| * | DEF_IN_DOM |
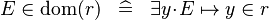 |
M | |
| * | DEF_IN_RAN |
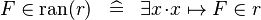 |
M | |
| * | DEF_IN_CONVERSE |
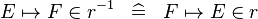 |
M | |
| * | DEF_IN_DOMRES |
 |
M | |
| * | DEF_IN_RANRES |
 |
M | |
| * | DEF_IN_DOMSUB |
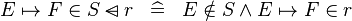 |
M | |
| * | DEF_IN_RANSUB |
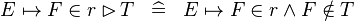 |
M | |
| * | DEF_IN_RELIMAGE |
![F \in r[w] \;\;\defi\;\; \exists x \qdot x \in w \land x \mapsto F \in r](/images/math/e/a/7/ea7840f0b824a8db50a6356a02b00904.png) |
M | |
| * | DEF_IN_FCOMP |
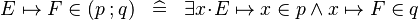 |
M | |
| * | DEF_OVERL |
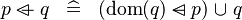 |
M | |
| * | DEF_IN_ID |
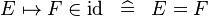 |
M | |
| * | DEF_IN_DPROD |
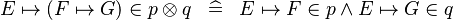 |
M | |
| * | DEF_IN_PPROD |
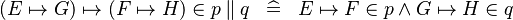 |
M | |
| * | DEF_IN_RELDOM |
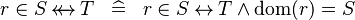 |
M | |
| * | DEF_IN_RELRAN |
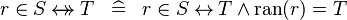 |
M | |
| * | DEF_IN_RELDOMRAN |
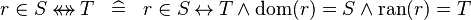 |
M | |
| * | DEF_IN_FCT |
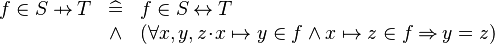 |
M | |
| * | DEF_IN_TFCT |
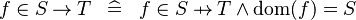 |
M | |
| * | DEF_IN_INJ |
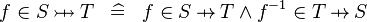 |
M | |
| * | DEF_IN_TINJ |
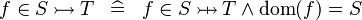 |
M | |
| * | DEF_IN_SURJ |
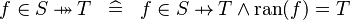 |
M | |
| * | DEF_IN_TSURJ |
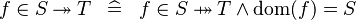 |
M | |
| * | DEF_IN_BIJ |
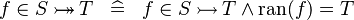 |
M | |
DISTRI_BCOMP_BUNION |
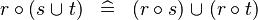 |
M | ||
| * | DISTRI_FCOMP_BUNION_R |
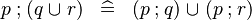 |
M | |
| * | DISTRI_FCOMP_BUNION_L |
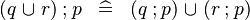 |
M | |
DISTRI_DPROD_BUNION |
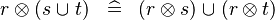 |
M | ||
DISTRI_DPROD_BINTER |
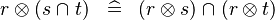 |
M | ||
DISTRI_DPROD_SETMINUS |
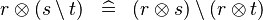 |
M | ||
DISTRI_DPROD_OVERL |
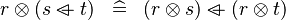 |
M | ||
DISTRI_PPROD_BUNION |
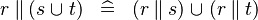 |
M | ||
DISTRI_PPROD_BINTER |
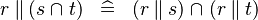 |
M | ||
DISTRI_PPROD_SETMINUS |
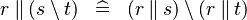 |
M | ||
DISTRI_PPROD_OVERL |
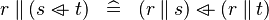 |
M | ||
DISTRI_OVERL_BUNION_L |
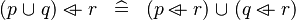 |
M | ||
DISTRI_OVERL_BINTER_L |
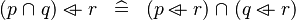 |
M | ||
| * | DISTRI_DOMRES_BUNION_R |
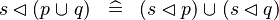 |
M | |
| * | DISTRI_DOMRES_BUNION_L |
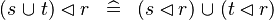 |
M | |
| * | DISTRI_DOMRES_BINTER_R |
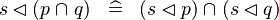 |
M | |
| * | DISTRI_DOMRES_BINTER_L |
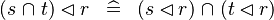 |
M | |
DISTRI_DOMRES_SETMINUS_R |
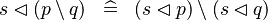 |
M | ||
DISTRI_DOMRES_SETMINUS_L |
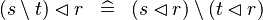 |
M | ||
DISTRI_DOMRES_DPROD |
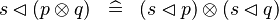 |
M | ||
DISTRI_DOMRES_OVERL |
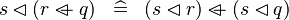 |
M | ||
| * | DISTRI_DOMSUB_BUNION_R |
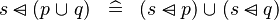 |
M | |
| b | DISTRI_DOMSUB_BUNION_L |
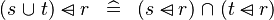 |
M | |
| * | DISTRI_DOMSUB_BINTER_R |
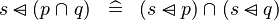 |
M | |
| b | DISTRI_DOMSUB_BINTER_L |
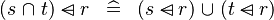 |
M | |
DISTRI_DOMSUB_DPROD |
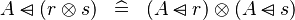 |
M | ||
DISTRI_DOMSUB_OVERL |
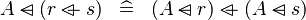 |
M | ||
| * | DISTRI_RANRES_BUNION_R |
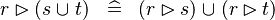 |
M | |
| * | DISTRI_RANRES_BUNION_L |
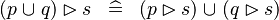 |
M | |
| * | DISTRI_RANRES_BINTER_R |
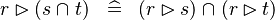 |
M | |
| * | DISTRI_RANRES_BINTER_L |
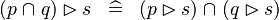 |
M | |
DISTRI_RANRES_SETMINUS_R |
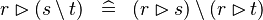 |
M | ||
DISTRI_RANRES_SETMINUS_L |
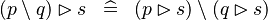 |
M | ||
| b | DISTRI_RANSUB_BUNION_R |
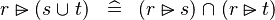 |
M | |
| * | DISTRI_RANSUB_BUNION_L |
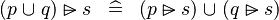 |
M | |
| b | DISTRI_RANSUB_BINTER_R |
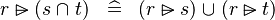 |
M | |
| * | DISTRI_RANSUB_BINTER_L |
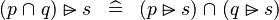 |
M | |
| * | DISTRI_CONVERSE_BUNION |
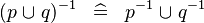 |
M | |
DISTRI_CONVERSE_BINTER |
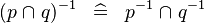 |
M | ||
DISTRI_CONVERSE_SETMINUS |
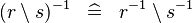 |
M | ||
DISTRI_CONVERSE_BCOMP |
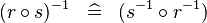 |
M | ||
DISTRI_CONVERSE_FCOMP |
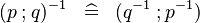 |
M | ||
DISTRI_CONVERSE_PPROD |
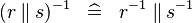 |
M | ||
DISTRI_CONVERSE_DOMRES |
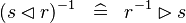 |
M | ||
DISTRI_CONVERSE_DOMSUB |
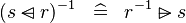 |
M | ||
DISTRI_CONVERSE_RANRES |
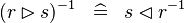 |
M | ||
DISTRI_CONVERSE_RANSUB |
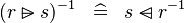 |
M | ||
| * | DISTRI_DOM_BUNION |
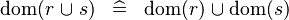 |
M | |
| * | DISTRI_RAN_BUNION |
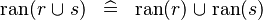 |
M | |
| * | DISTRI_RELIMAGE_BUNION_R |
![r[S \bunion T] \;\;\defi\;\; r[S] \bunion r[T]](/images/math/6/7/5/675105d6ac145c32895450ddb1a9515f.png) |
M | |
| * | DISTRI_RELIMAGE_BUNION_L |
![(p \bunion q)[S] \;\;\defi\;\; p[S] \bunion q[S]](/images/math/c/d/a/cdad0c6221ccb102d4f674695d7ff79c.png) |
M | |
| * | DISTRI_DOM_BUNION |
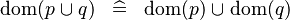 |
M | |
| * | DISTRI_RAN_BUNION |
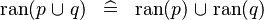 |
M | |
| * | DERIV_DOM_TOTALREL |
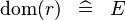 |
with hypothesis 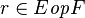 , where , where 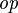 is one of is one of 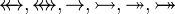 |
M |
DERIV_RAN_SURJREL |
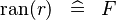 |
with hypothesis 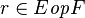 , where , where 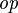 is one of is one of 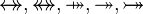 |
M | |
prjone-total |
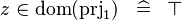 |
A | ||
prjtwo-total |
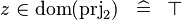 |
A | ||
prjone-functional |
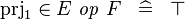 |
where \mathit{op} is one of 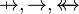 |
A | |
prjtwo-functional |
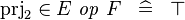 |
where \mathit{op} is one of 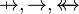 |
A | |
prj-expand |
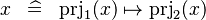 |
M |