Rewriting rules for event model decomposition: Difference between revisions
imported>Pascal |
imported>Pascal |
||
| Line 69: | Line 69: | ||
== Transformation rules == | == Transformation rules == | ||
The transformation from a given Event-B action to another is subsequently be represented with the <math>\rightsquigarrow</math> symbol. <math> | The transformation from a given Event-B action of a sub-machine <math>M_i</math> to another action of a sub-machine <math>M_j</math> is subsequently be represented with the <math>\rightsquigarrow</math> symbol. <math>s</math> and <math>t</math> are assumed to be variables shared between <math>M_i</math> and <math>M_j</math>, <math>v</math> and <math>w</math> other variables, <math>E</math> and <math>F</math> expressions, and <math>P</math> and <math>Q</math> before-after predicates. | ||
<br>Let's first establish a transformation rule for generic Event-B assignments. It is then possible to deduce transformation rules for other assignments of the Event-B language. | <br>Let's first establish a transformation rule for generic Event-B assignments. It is then possible to deduce transformation rules for other assignments of the Event-B language. | ||
Revision as of 15:09, 22 July 2009
The purpose of this page is to list and justify the transformation rules applied in the event model decomposition, when building the actions of an external event of a sub-machine from those of an initial event in the non-decomposed machine.
Equivalence and simplification rules
It is first necessary to introduce some equivalence and simplification rules on Event-B assignments and predicates. These rules will then help to understand the transformation rules to be applied to build the actions of the external events.
Equivalence relation
It is possible to define an equivalence relation on the Event-B actions, and by restriction on the Event-B assignments. Two actions are considered as being equivalent if the proof obligations generated for these actions are logically equivalent.
This relation is represented with the 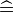 symbol.
symbol.
Equivalence rules on Event-B assignments
As detailed in the modelling language, the Event-B assignments are formed of two parts:
- A left-hand side, which is a list of free identifiers.
- A right-hand side.
There are various kinds of assignments:
- The
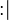 ("becomes such that") assignment is the most general (non-deterministic) assignment, where a predicate is given on the before and after values of assigned identifiers. The after values of the assigned identifiers are denoted by a primed identifier whose prefix is the assigned identifier.
("becomes such that") assignment is the most general (non-deterministic) assignment, where a predicate is given on the before and after values of assigned identifiers. The after values of the assigned identifiers are denoted by a primed identifier whose prefix is the assigned identifier. - The
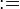 ("becomes equal to") assignment is the deterministic assignment where an expression is given for each assigned identifier.
("becomes equal to") assignment is the deterministic assignment where an expression is given for each assigned identifier. - The
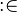 ("becomes member of") assignment is the set-based (non-deterministic) assignment, where a set expression is given for the assigned identifier.
("becomes member of") assignment is the set-based (non-deterministic) assignment, where a set expression is given for the assigned identifier.
Let 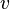 and
and 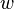 be variables, and
be variables, and  and
and 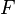 be expressions. In the following table, the left-hand assignments are equivalent (
be expressions. In the following table, the left-hand assignments are equivalent (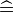 ) to the right-hand ones (see the B-book):
) to the right-hand ones (see the B-book):
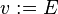 |
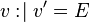 |
Rule 1 |
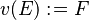 |
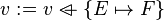 |
Rule 2 |
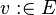 |
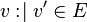 |
Rule 3 |
Equivalence rules on Event-B actions
Let 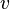 and
and 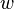 be variables,
be variables,  and
and 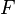 be expressions, and
be expressions, and 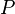 and
and 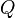 be predicates. The left-hand actions are equivalent (
be predicates. The left-hand actions are equivalent (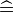 ) to the right-hand ones:
) to the right-hand ones:
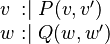 |
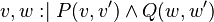 |
Rule 4 |
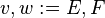 |
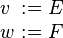 |
Rule 5 |
Note 1: The 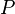 predicate can refer to other before variables than
predicate can refer to other before variables than 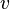 (e.g.
(e.g. 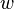 or
or 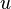 , where
, where 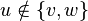 ). Similarly,
). Similarly, 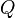 can refer to other variables than
can refer to other variables than 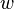 .
.
Note 2: The following equivalence is obtained by enforcing the rules 1 and 4, and is a good replacement for the rule 5:
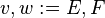 |
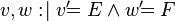 |
Rule 5 |
Simplification rules on Event-B predicates
Let 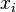 ,
, 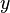 and
and 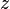 be variables, and
be variables, and 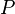 and
and 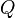 be predicates.
be predicates.
- Rule 6: If
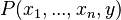 is equal to
is equal to 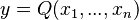 , then the
, then the 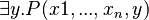 predicate is true, and it may be deleted in conjunctive predicates (
predicate is true, and it may be deleted in conjunctive predicates (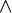 ) where it appears.
) where it appears. - Rule 7: The
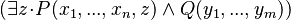 predicate, where
predicate, where 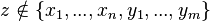 , may be rewritten as
, may be rewritten as 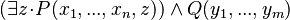 .
. - Rule 8: The
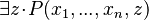 predicate may be deleted in conjunctive predicates where it appears if the
predicate may be deleted in conjunctive predicates where it appears if the 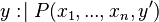 assignment is among the actions of the initial event. It indeed is nothing else but the feasibility (FIS) proof obligation for such an assignment, and a model to be decomposed is assumed to be proved (see the section related to the proof obligations in the event model decomposition).
assignment is among the actions of the initial event. It indeed is nothing else but the feasibility (FIS) proof obligation for such an assignment, and a model to be decomposed is assumed to be proved (see the section related to the proof obligations in the event model decomposition).
Example
Let 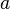 ,
, 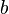 and
and  be variables, and
be variables, and 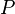 and
and 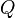 be predicates.
be predicates.
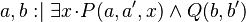
|
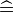 (Rule 7) (Rule 7) |
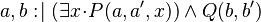
|
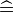 (Rule 4) (Rule 4) |
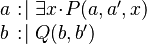
|
Transformation rules
The transformation from a given Event-B action of a sub-machine 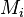 to another action of a sub-machine
to another action of a sub-machine 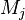 is subsequently be represented with the
is subsequently be represented with the 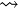 symbol.
symbol.  and
and  are assumed to be variables shared between
are assumed to be variables shared between 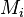 and
and 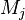 ,
, 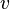 and
and 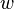 other variables,
other variables,  and
and 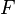 expressions, and
expressions, and 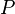 and
and 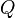 before-after predicates.
before-after predicates.
Let's first establish a transformation rule for generic Event-B assignments. It is then possible to deduce transformation rules for other assignments of the Event-B language.
Generic transformation rule on Event-B assignments
The generic transformation rule on Event-B assignments is defined below:
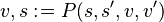 |
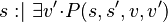 |
Rule 9 |
Derived transformation rules on Event-B assignments
The transformation rules for other Event-B assignments are obtained by applying the generic rule and the equivalence / simplification rules previously introduced. More precisely:
- The equivalence rules 1 to 5 shall be first applied as many times as possible, from left to right, to get the assignment into the generic form.
- Then, generic transformation rule 9 shall be enforced.
- Then, the simplification rules 6 to 8 shall be enforced.
- Finally, the equivalence rules 1 to 3 shall be applied, from right to left. The proof obligations generated for deterministic actions are indeed more suitable than those generated for non-deterministic actions. In the same manner, for a given set
 , proving that
, proving that 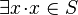 (FIS proof obligation generated from
(FIS proof obligation generated from 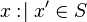 ) is indeed not as "simple" as proving that
) is indeed not as "simple" as proving that 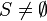 (proof obligation generated from
(proof obligation generated from 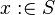 ).
).
Example
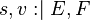
|
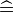 (Rule 5) (Rule 5) |
|
 (Rule 9) (Rule 9) |
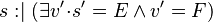
|
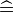 (Rule 7) (Rule 7) |
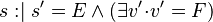
|
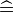 (Rule 6) (Rule 6) |
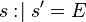
|
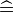 (Rule 1) (Rule 1) |
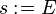
|
Formalization
The derived transformation rules on Event-B assignments are listed below:
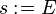 |
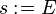 |
Rule 10 |
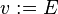 |
(empty) | Rule 11 |
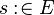 |
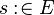 |
Rule 12 |
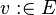 |
(empty) | Rule 13 |
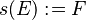 |
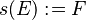 |
Rule 14 |
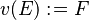 |
(empty) | Rule 15 |
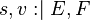 |
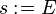 |
Rule 16 |
Derived transformation rules on Event-B actions
The transformation can be done separately for each assignment of an Event-B action, as demonstrated below:
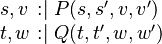
|
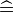 (Rule 4) (Rule 4) |
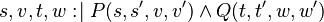
|
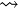 (Rule 9) (Rule 9) |
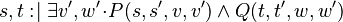
|
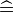 (Rule 7) (Rule 7) |
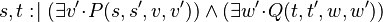
|
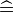 (Rule 4) (Rule 4) |
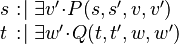
|