Arithmetic Rewrite Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Frederic New page: {{RRHeader}} {{RRRow}}|<font size="-2"> SIMP_SPECIAL_MOD_0 </font>||<math> 0 \,\bmod\, E \;\;\defi\;\; 0 </math>|| || A {{RRRow}}|<font size="-2"> SIMP_SPECIAL_MOD_1 </font>||<math> ... |
imported>Laurent Added star column |
||
| Line 1: | Line 1: | ||
{{RRHeader}} | {{RRHeader}} | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_MOD_0 </font>||<math> 0 \,\bmod\, E \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}| ||<font size="-2"> SIMP_SPECIAL_MOD_0 </font>||<math> 0 \,\bmod\, E \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_MOD_1 </font>||<math> E \mod 1 \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}| ||<font size="-2"> SIMP_SPECIAL_MOD_1 </font>||<math> E \mod 1 \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MIN_SING </font>||<math> \min (\{ E\} ) \;\;\defi\;\; E </math>|| where <math>E</math> is a single expression || A | {{RRRow}}|*||<font size="-2"> SIMP_MIN_SING </font>||<math> \min (\{ E\} ) \;\;\defi\;\; E </math>|| where <math>E</math> is a single expression || A | ||
{{RRRow}}|<font size="-2"> SIMP_MAX_SING </font>||<math> \max (\{ E\} ) \;\;\defi\;\; E </math>|| where <math>E</math> is a single expression || A | {{RRRow}}|*||<font size="-2"> SIMP_MAX_SING </font>||<math> \max (\{ E\} ) \;\;\defi\;\; E </math>|| where <math>E</math> is a single expression || A | ||
{{RRRow}}|<font size="-2"> SIMP_MIN_NATURAL </font>||<math> \min (\nat ) \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MIN_NATURAL </font>||<math> \min (\nat ) \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MIN_NATURAL1 </font>||<math> \min (\natn ) \;\;\defi\;\; 1 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MIN_NATURAL1 </font>||<math> \min (\natn ) \;\;\defi\;\; 1 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MIN_BUNION_SING </font>||<math> \begin{array}{cl} & \min (S \bunion \ldots \bunion \{ \min (T)\} \bunion \ldots \bunion U) \\ \defi & \min (S \bunion \ldots \bunion T \bunion \ldots \bunion U) \\ \end{array} </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MIN_BUNION_SING </font>||<math> \begin{array}{cl} & \min (S \bunion \ldots \bunion \{ \min (T)\} \bunion \ldots \bunion U) \\ \defi & \min (S \bunion \ldots \bunion T \bunion \ldots \bunion U) \\ \end{array} </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MAX_BUNION_SING </font>||<math> \begin{array}{cl} & \max (S \bunion \ldots \bunion \{ \max (T)\} \bunion \ldots \bunion U) \\ \defi & \max (S \bunion \ldots \bunion T \bunion \ldots \bunion U) \\ \end{array} </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MAX_BUNION_SING </font>||<math> \begin{array}{cl} & \max (S \bunion \ldots \bunion \{ \max (T)\} \bunion \ldots \bunion U) \\ \defi & \max (S \bunion \ldots \bunion T \bunion \ldots \bunion U) \\ \end{array} </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MIN_UPTO </font>||<math> \min (E \upto F) \;\;\defi\;\; E </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MIN_UPTO </font>||<math> \min (E \upto F) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MAX_UPTO </font>||<math> \max (E \upto F) \;\;\defi\;\; F </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MAX_UPTO </font>||<math> \max (E \upto F) \;\;\defi\;\; F </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_MIN </font>||<math> \min (\{ E, \ldots , i, \ldots , j, \ldots , H\} ) \;\;\defi\;\; \min (\{ E, \ldots , i, \ldots , H\} ) </math>|| where <math>i</math> and <math>j</math> are literals and <math>i \leq j</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_MIN </font>||<math> \min (\{ E, \ldots , i, \ldots , j, \ldots , H\} ) \;\;\defi\;\; \min (\{ E, \ldots , i, \ldots , H\} ) </math>|| where <math>i</math> and <math>j</math> are literals and <math>i \leq j</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_MAX </font>||<math> \max (\{ E, \ldots , i, \ldots , j, \ldots , H\} ) \;\;\defi\;\; \max (\{ E, \ldots , i, \ldots , H\} ) </math>|| where <math>i</math> and <math>j</math> are literals and <math>i \geq j</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_MAX </font>||<math> \max (\{ E, \ldots , i, \ldots , j, \ldots , H\} ) \;\;\defi\;\; \max (\{ E, \ldots , i, \ldots , H\} ) </math>|| where <math>i</math> and <math>j</math> are literals and <math>i \geq j</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_MIN_UPTO </font>||<math> \min (\{ i, \ldots , j\} ) \;\;\defi\;\; A \;\;(computation) </math>|| where <math>i, ... ,\,j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_MIN_UPTO </font>||<math> \min (\{ i, \ldots , j\} ) \;\;\defi\;\; A \;\;(computation) </math>|| where <math>i, ... ,\,j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_MAX_UPTO </font>||<math> \max (\{ i, \ldots , j\} ) \;\;\defi\;\; A \;\;(computation) </math>|| where <math>i, ... ,\,j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_MAX_UPTO </font>||<math> \max (\{ i, \ldots , j\} ) \;\;\defi\;\; A \;\;(computation) </math>|| where <math>i, ... ,\,j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_CARD </font>||<math> \card (\emptyset ) \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_CARD </font>||<math> \card (\emptyset ) \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_SING </font>||<math> \card (\{ E\} ) \;\;\defi\;\; 1 </math>|| where <math>E</math> is a single expression || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_SING </font>||<math> \card (\{ E\} ) \;\;\defi\;\; 1 </math>|| where <math>E</math> is a single expression || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_EQUAL_CARD </font>||<math> \card (S) = 0 \;\;\defi\;\; S = \emptyset </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_EQUAL_CARD </font>||<math> \card (S) = 0 \;\;\defi\;\; S = \emptyset </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_POW </font>||<math> \card (\pow (S)) \;\;\defi\;\; 2 ^ \card (S) </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_POW </font>||<math> \card (\pow (S)) \;\;\defi\;\; 2 ^ \card (S) </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_BUNION </font>||<math> \card (S \bunion T) \;\;\defi\;\; \card (S) + \card (T) - \card (S \binter T) </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_BUNION </font>||<math> \card (S \bunion T) \;\;\defi\;\; \card (S) + \card (T) - \card (S \binter T) </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_CONVERSE </font>||<math> \card (r^{-1} ) \;\;\defi\;\; \card (r) </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_CONVERSE </font>||<math> \card (r^{-1} ) \;\;\defi\;\; \card (r) </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_ID </font>||<math> \card (\id (S)) \;\;\defi\;\; \card (S) </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_ID </font>||<math> \card (\id (S)) \;\;\defi\;\; \card (S) </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_LAMBDA </font>||<math> \card (\lambda x\qdot (P \mid E)) \;\;\defi\;\; \card (\{ x \qdot P \mid x\} ) </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_LAMBDA </font>||<math> \card (\lambda x\qdot (P \mid E)) \;\;\defi\;\; \card (\{ x \qdot P \mid x\} ) </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_COMPSET </font>||<math> \card (\{ x \qdot x \in S \mid x\} ) \;\;\defi\;\; \card (S) </math>|| where <math>x</math> non free in <math>S</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_COMPSET </font>||<math> \card (\{ x \qdot x \in S \mid x\} ) \;\;\defi\;\; \card (S) </math>|| where <math>x</math> non free in <math>S</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_CARD_UPTO </font>||<math> \card (i \upto j) \;\;\defi\;\; j-i+1 </math>|| where <math>i</math> and <math>j</math> are literals and <math>i \leq j</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_CARD_UPTO </font>||<math> \card (i \upto j) \;\;\defi\;\; j-i+1 </math>|| where <math>i</math> and <math>j</math> are literals and <math>i \leq j</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_TYPE_CARD </font>||<math> \card (\mathit{Tenum}) \;\;\defi\;\; N </math>|| where <math>\mathit{Tenum}</math> is a carrier set containing <math>N</math> elements || A | {{RRRow}}|*||<font size="-2"> SIMP_TYPE_CARD </font>||<math> \card (\mathit{Tenum}) \;\;\defi\;\; N </math>|| where <math>\mathit{Tenum}</math> is a carrier set containing <math>N</math> elements || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_GE_CARD_0 </font>||<math> \card (S) \geq 1 \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_GE_CARD_0 </font>||<math> \card (S) \geq 1 \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_LE_CARD_1 </font>||<math> 1 \leq \card (S) \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_LE_CARD_1 </font>||<math> 1 \leq \card (S) \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_LE_CARD_0 </font>||<math> 0 \leq \card (S) \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_LE_CARD_0 </font>||<math> 0 \leq \card (S) \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_GE_CARD_0 </font>||<math> \card (S) \geq 0 \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_GE_CARD_0 </font>||<math> \card (S) \geq 0 \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_GT_CARD_0 </font>||<math> \card (S) > 0 \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_GT_CARD_0 </font>||<math> \card (S) > 0 \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_LT_CARD_0 </font>||<math> 0 < \card (S) \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_LT_CARD_0 </font>||<math> 0 < \card (S) \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_EQUAL_CARD_1 </font>||<math> \card (S) = 1 \;\;\defi\;\; \exists x \qdot S = \{ x\} </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_EQUAL_CARD_1 </font>||<math> \card (S) = 1 \;\;\defi\;\; \exists x \qdot S = \{ x\} </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_NATURAL </font>||<math> \card (S) \in \nat \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_NATURAL </font>||<math> \card (S) \in \nat \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_CARD_NATURAL1 </font>||<math> \card (S) \in \natn \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_CARD_NATURAL1 </font>||<math> \card (S) \in \natn \;\;\defi\;\; \lnot\, S = \emptyset </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_IN_NATURAL </font>||<math> i \in \nat \;\;\defi\;\; \btrue </math>|| where <math>i</math> is a literal || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_IN_NATURAL </font>||<math> i \in \nat \;\;\defi\;\; \btrue </math>|| where <math>i</math> is a literal || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_IN_NATURAL1 </font>||<math> 0 \in \natn \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}| ||<font size="-2"> SIMP_SPECIAL_IN_NATURAL1 </font>||<math> 0 \in \natn \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_IN_NATURAL1 </font>||<math> i \in \natn \;\;\defi\;\; \btrue </math>|| where <math>i</math> is a literal and <math>1 \leq i</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_IN_NATURAL1 </font>||<math> i \in \natn \;\;\defi\;\; \btrue </math>|| where <math>i</math> is a literal and <math>1 \leq i</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_UPTO </font>||<math> i \upto j \;\;\defi\;\; \emptyset </math>|| where <math>i</math> and <math>j</math> are literals and <math>j < i</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_UPTO </font>||<math> i \upto j \;\;\defi\;\; \emptyset </math>|| where <math>i</math> and <math>j</math> are literals and <math>j < i</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_IN_MINUS_NATURAL </font>||<math> -i \in \nat \;\;\defi\;\; \bfalse </math>|| where <math>i</math> is a literal and <math>1 \leq i</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_IN_MINUS_NATURAL </font>||<math> -i \in \nat \;\;\defi\;\; \bfalse </math>|| where <math>i</math> is a literal and <math>1 \leq i</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_IN_MINUS_NATURAL1 </font>||<math> -i \in \natn \;\;\defi\;\; \bfalse </math>|| where <math>i</math> is a literal || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_IN_MINUS_NATURAL1 </font>||<math> -i \in \natn \;\;\defi\;\; \bfalse </math>|| where <math>i</math> is a literal || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_KBOOL_BTRUE </font>||<math> \bool (\btrue ) \;\;\defi\;\; \True </math>|| || A | {{RRRow}}| ||<font size="-2"> SIMP_SPECIAL_KBOOL_BTRUE </font>||<math> \bool (\btrue ) \;\;\defi\;\; \True </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_KBOOL_BFALSE </font>||<math> \bool (\bfalse ) \;\;\defi\;\; \False </math>|| || A | {{RRRow}}| ||<font size="-2"> SIMP_SPECIAL_KBOOL_BFALSE </font>||<math> \bool (\bfalse ) \;\;\defi\;\; \False </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_EQUAL_KBOOL_TRUE </font>||<math> \bool (P) = \True \;\;\defi\;\; P </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_EQUAL_KBOOL_TRUE </font>||<math> \bool (P) = \True \;\;\defi\;\; P </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_EQUAL_KBOOL_FALSE </font>||<math> \bool (P) = \False \;\;\defi\;\; \lnot\, P </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_EQUAL_KBOOL_FALSE </font>||<math> \bool (P) = \False \;\;\defi\;\; \lnot\, P </math>|| || A | ||
{{RRRow}}|<font size="-2"> DEF_EQUAL_MIN </font>||<math> E = \min (S) \;\;\defi\;\; E \in S \land (\forall x \qdot x \in S \limp E \leq x) </math>|| where <math>x</math> non free in <math>S, E</math> || M | {{RRRow}}|*||<font size="-2"> DEF_EQUAL_MIN </font>||<math> E = \min (S) \;\;\defi\;\; E \in S \land (\forall x \qdot x \in S \limp E \leq x) </math>|| where <math>x</math> non free in <math>S, E</math> || M | ||
{{RRRow}}|<font size="-2"> DEF_EQUAL_MAX </font>||<math> E = \max (S) \;\;\defi\;\; E \in S \land (\forall x \qdot x \in S \limp E \geq x) </math>|| where <math>x</math> non free in <math>S, E</math> || M | {{RRRow}}|*||<font size="-2"> DEF_EQUAL_MAX </font>||<math> E = \max (S) \;\;\defi\;\; E \in S \land (\forall x \qdot x \in S \limp E \geq x) </math>|| where <math>x</math> non free in <math>S, E</math> || M | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_PLUS </font>||<math> E + \ldots + 0 + \ldots + F \;\;\defi\;\; E + \ldots + F </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_PLUS </font>||<math> E + \ldots + 0 + \ldots + F \;\;\defi\;\; E + \ldots + F </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_MINUS_R </font>||<math> E - 0 \;\;\defi\;\; E </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_MINUS_R </font>||<math> E - 0 \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_MINUS_L </font>||<math> 0 - E \;\;\defi\;\; -E </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_MINUS_L </font>||<math> 0 - E \;\;\defi\;\; -E </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MINUS_MINUS </font>||<math> - (- E) \;\;\defi\;\; E </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MINUS_MINUS </font>||<math> - (- E) \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_MINUS </font>||<math> E - E \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_PROD_0 </font>||<math> E * \ldots * 0 * \ldots * F \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_PROD_0 </font>||<math> E * \ldots * 0 * \ldots * F \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_PROD_1 </font>||<math> E * \ldots * 1 * \ldots * F \;\;\defi\;\; E * \ldots * F </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_PROD_1 </font>||<math> E * \ldots * 1 * \ldots * F \;\;\defi\;\; E * \ldots * F </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_PROD_MINUS_EVEN </font>||<math> (-E) * \ldots * (-F) \;\;\defi\;\; E * \ldots * F </math>|| if an even number of <math>-</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_PROD_MINUS_EVEN </font>||<math> (-E) * \ldots * (-F) \;\;\defi\;\; E * \ldots * F </math>|| if an even number of <math>-</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_PROD_MINUS_ODD </font>||<math> (-E) * \ldots * (-F) \;\;\defi\;\; -(E * \ldots * F) </math>|| if an odd number of <math>-</math> || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_PROD_MINUS_ODD </font>||<math> (-E) * \ldots * (-F) \;\;\defi\;\; -(E * \ldots * F) </math>|| if an odd number of <math>-</math> || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_MINUS </font>||<math> - (i) \;\;\defi\;\; (-i) </math>|| where <math>i</math> is a literal || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_MINUS </font>||<math> - (i) \;\;\defi\;\; (-i) </math>|| where <math>i</math> is a literal || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_MINUS_MINUS </font>||<math> - (-i) \;\;\defi\;\; i </math>|| where <math>i</math> is a literal || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_MINUS_MINUS </font>||<math> - (-i) \;\;\defi\;\; i </math>|| where <math>i</math> is a literal || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_EQUAL </font>||<math> <math>i = j<math> \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_EQUAL </font>||<math> <math>i = j<math> \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_LE </font>||<math> i \leq j \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_LE </font>||<math> i \leq j \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_LT </font>||<math> i < j \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_LT </font>||<math> i < j \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_GE </font>||<math> i \geq j \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_GE </font>||<math> i \geq j \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_LIT_GT </font>||<math> <math>i > j<math> \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | {{RRRow}}|*||<font size="-2"> SIMP_LIT_GT </font>||<math> <math>i > j<math> \;\;\defi\;\; \btrue \;or\; \bfalse \;\;(computation) </math>|| where <math>i</math> and <math>j</math> are literals || A | ||
{{RRRow}}|<font size="-2"> SIMP_DIV_MINUS </font>||<math> (- E) \div (-F) \;\;\defi\;\; E \div F </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_DIV_MINUS </font>||<math> (- E) \div (-F) \;\;\defi\;\; E \div F </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_DIV_1 </font>||<math> E \div 1 \;\;\defi\;\; E </math>|| || A | {{RRRow}}| ||<font size="-2"> SIMP_SPECIAL_DIV_1 </font>||<math> E \div 1 \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_DIV_0 </font>||<math> 0 \div E \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_DIV_0 </font>||<math> 0 \div E \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_EXPN_1 </font>||<math> E ^ 1 \;\;\defi\;\; E </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_EXPN_1 </font>||<math> E ^ 1 \;\;\defi\;\; E </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_SPECIAL_EXPN_0 </font>||<math> E ^ 0 \;\;\defi\;\; 1 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_SPECIAL_EXPN_0 </font>||<math> E ^ 0 \;\;\defi\;\; 1 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MULTI_LE </font>||<math> E \leq E \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_LE </font>||<math> E \leq E \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MULTI_LT </font>||<math> E < E \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_LT </font>||<math> E < E \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MULTI_GE </font>||<math> E \geq E \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_GE </font>||<math> E \geq E \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MULTI_GT </font>||<math> E > E \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_GT </font>||<math> E > E \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MULTI_DIV </font>||<math> E \div E \;\;\defi\;\; 1 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_DIV </font>||<math> E \div E \;\;\defi\;\; 1 </math>|| || A | ||
{{RRRow}}|<font size="-2"> SIMP_MULTI_MOD </font>||<math> E \mod E \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}|*||<font size="-2"> SIMP_MULTI_MOD </font>||<math> E \mod E \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|<font size="-2"> DISTRI_PROD_PLUS </font>||<math> a * (b + c) \;\;\defi\;\; (a * b) + (a * c) </math>|| || M | {{RRRow}}|*||<font size="-2"> DISTRI_PROD_PLUS </font>||<math> a * (b + c) \;\;\defi\;\; (a * b) + (a * c) </math>|| || M | ||
{{RRRow}}|<font size="-2"> DISTRI_PROD_MINUS </font>||<math> a * (b - c) \;\;\defi\;\; (a * b) - (a * c) </math>|| || M | {{RRRow}}|*||<font size="-2"> DISTRI_PROD_MINUS </font>||<math> a * (b - c) \;\;\defi\;\; (a * b) - (a * c) </math>|| || M | ||
{{RRRow}}|<font size="-2"> DERIV_LE_CARD </font>||<math> \card (S) \leq \card (T) \;\;\defi\;\; S \subseteq T </math>|| <math>S</math> and <math>T</math> must be of the same type || M | {{RRRow}}|*||<font size="-2"> DERIV_LE_CARD </font>||<math> \card (S) \leq \card (T) \;\;\defi\;\; S \subseteq T </math>|| <math>S</math> and <math>T</math> must be of the same type || M | ||
{{RRRow}}|<font size="-2"> DERIV_GE_CARD </font>||<math> \card (S) \geq \card (T) \;\;\defi\;\; T \subseteq S </math>|| <math>S</math> and <math>T</math> must be of the same type || M | {{RRRow}}|*||<font size="-2"> DERIV_GE_CARD </font>||<math> \card (S) \geq \card (T) \;\;\defi\;\; T \subseteq S </math>|| <math>S</math> and <math>T</math> must be of the same type || M | ||
{{RRRow}}|<font size="-2"> DERIV_LT_CARD </font>||<math> \card (S) < \card (T) \;\;\defi\;\; S \subset T </math>|| <math>S</math> and <math>T</math> must be of the same type || M | {{RRRow}}|*||<font size="-2"> DERIV_LT_CARD </font>||<math> \card (S) < \card (T) \;\;\defi\;\; S \subset T </math>|| <math>S</math> and <math>T</math> must be of the same type || M | ||
{{RRRow}}|<font size="-2"> DERIV_GT_CARD </font>||<math> \card (S) > \card (T) \;\;\defi\;\; T \subset S </math>|| <math>S</math> and <math>T</math> must be of the same type || M | {{RRRow}}|*||<font size="-2"> DERIV_GT_CARD </font>||<math> \card (S) > \card (T) \;\;\defi\;\; T \subset S </math>|| <math>S</math> and <math>T</math> must be of the same type || M | ||
{{RRRow}}|<font size="-2"> DERIV_EQUAL_CARD </font>||<math> \card (S) = \card (T) \;\;\defi\;\; S = T </math>|| <math>S</math> and <math>T</math> must be of the same type || M | {{RRRow}}|*||<font size="-2"> DERIV_EQUAL_CARD </font>||<math> \card (S) = \card (T) \;\;\defi\;\; S = T </math>|| <math>S</math> and <math>T</math> must be of the same type || M | ||
|} | |} | ||
Revision as of 17:06, 11 February 2009
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| SIMP_SPECIAL_MOD_0 | 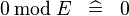 |
A | ||
| SIMP_SPECIAL_MOD_1 | 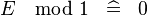 |
A | ||
| * | SIMP_MIN_SING | 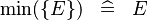 |
where  is a single expression is a single expression |
A |
| * | SIMP_MAX_SING | 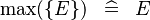 |
where  is a single expression is a single expression |
A |
| * | SIMP_MIN_NATURAL | 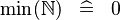 |
A | |
| * | SIMP_MIN_NATURAL1 | 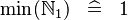 |
A | |
| * | SIMP_MIN_BUNION_SING | 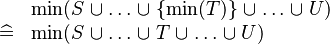 |
A | |
| * | SIMP_MAX_BUNION_SING | 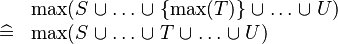 |
A | |
| * | SIMP_MIN_UPTO | 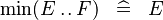 |
A | |
| * | SIMP_MAX_UPTO | 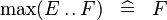 |
A | |
| * | SIMP_LIT_MIN | 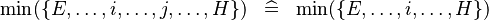 |
where  and and  are literals and are literals and 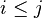 |
A |
| * | SIMP_LIT_MAX | 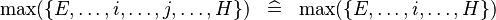 |
where  and and  are literals and are literals and 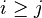 |
A |
| * | SIMP_LIT_MIN_UPTO | 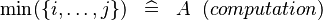 |
where 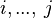 are literals are literals |
A |
| * | SIMP_LIT_MAX_UPTO | 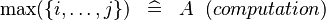 |
where 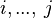 are literals are literals |
A |
| * | SIMP_SPECIAL_CARD | 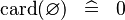 |
A | |
| * | SIMP_CARD_SING | 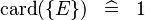 |
where  is a single expression is a single expression |
A |
| * | SIMP_SPECIAL_EQUAL_CARD | 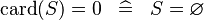 |
A | |
| * | SIMP_CARD_POW | 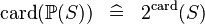 |
A | |
| * | SIMP_CARD_BUNION | 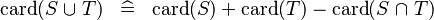 |
A | |
| * | SIMP_CARD_CONVERSE | 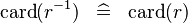 |
A | |
| * | SIMP_CARD_ID | 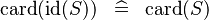 |
A | |
| * | SIMP_CARD_LAMBDA | 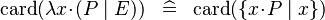 |
A | |
| * | SIMP_CARD_COMPSET | 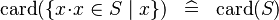 |
where  non free in non free in  |
A |
| * | SIMP_LIT_CARD_UPTO | 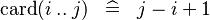 |
where  and and  are literals and are literals and 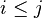 |
A |
| * | SIMP_TYPE_CARD | 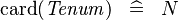 |
where 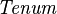 is a carrier set containing is a carrier set containing 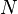 elements elements |
A |
| * | SIMP_LIT_GE_CARD_0 | 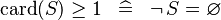 |
A | |
| * | SIMP_LIT_LE_CARD_1 | 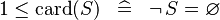 |
A | |
| * | SIMP_LIT_LE_CARD_0 | 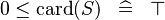 |
A | |
| * | SIMP_LIT_GE_CARD_0 | 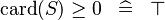 |
A | |
| * | SIMP_LIT_GT_CARD_0 | 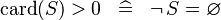 |
A | |
| * | SIMP_LIT_LT_CARD_0 | 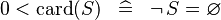 |
A | |
| * | SIMP_LIT_EQUAL_CARD_1 | 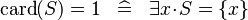 |
A | |
| * | SIMP_CARD_NATURAL | 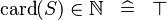 |
A | |
| * | SIMP_CARD_NATURAL1 | 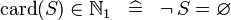 |
A | |
| * | SIMP_LIT_IN_NATURAL |  |
where  is a literal is a literal |
A |
| SIMP_SPECIAL_IN_NATURAL1 | 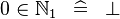 |
A | ||
| * | SIMP_LIT_IN_NATURAL1 | 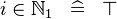 |
where  is a literal and is a literal and 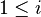 |
A |
| * | SIMP_LIT_UPTO | 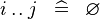 |
where  and and  are literals and are literals and 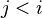 |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL | 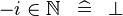 |
where  is a literal and is a literal and 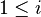 |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL1 | 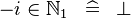 |
where  is a literal is a literal |
A |
| SIMP_SPECIAL_KBOOL_BTRUE | 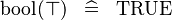 |
A | ||
| SIMP_SPECIAL_KBOOL_BFALSE | 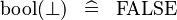 |
A | ||
| * | SIMP_LIT_EQUAL_KBOOL_TRUE | 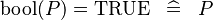 |
A | |
| * | SIMP_LIT_EQUAL_KBOOL_FALSE | 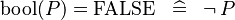 |
A | |
| * | DEF_EQUAL_MIN | 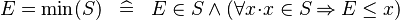 |
where  non free in non free in 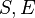 |
M |
| * | DEF_EQUAL_MAX | 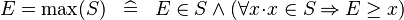 |
where  non free in non free in 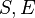 |
M |
| * | SIMP_SPECIAL_PLUS | 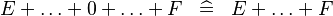 |
A | |
| * | SIMP_SPECIAL_MINUS_R |  |
A | |
| * | SIMP_SPECIAL_MINUS_L | 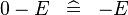 |
A | |
| * | SIMP_MINUS_MINUS | 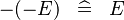 |
A | |
| * | SIMP_MULTI_MINUS | 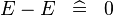 |
A | |
| * | SIMP_SPECIAL_PROD_0 | 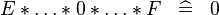 |
A | |
| * | SIMP_SPECIAL_PROD_1 | 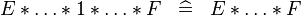 |
A | |
| * | SIMP_SPECIAL_PROD_MINUS_EVEN | 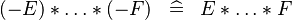 |
if an even number of  |
A |
| * | SIMP_SPECIAL_PROD_MINUS_ODD | 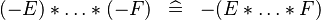 |
if an odd number of  |
A |
| * | SIMP_LIT_MINUS | 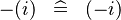 |
where  is a literal is a literal |
A |
| * | SIMP_LIT_MINUS_MINUS | 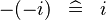 |
where  is a literal is a literal |
A |
| * | SIMP_LIT_EQUAL | 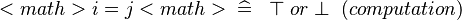 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_LE | 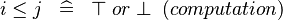 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_LT | 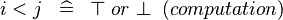 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_GE | 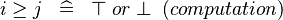 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_GT | 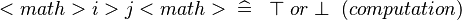 |
where  and and  are literals are literals |
A |
| * | SIMP_DIV_MINUS | 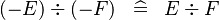 |
A | |
| SIMP_SPECIAL_DIV_1 |  |
A | ||
| * | SIMP_SPECIAL_DIV_0 | 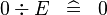 |
A | |
| * | SIMP_SPECIAL_EXPN_1 | 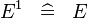 |
A | |
| * | SIMP_SPECIAL_EXPN_0 | 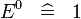 |
A | |
| * | SIMP_MULTI_LE | 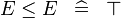 |
A | |
| * | SIMP_MULTI_LT | 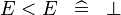 |
A | |
| * | SIMP_MULTI_GE | 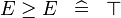 |
A | |
| * | SIMP_MULTI_GT | 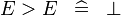 |
A | |
| * | SIMP_MULTI_DIV | 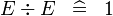 |
A | |
| * | SIMP_MULTI_MOD | 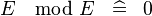 |
A | |
| * | DISTRI_PROD_PLUS | 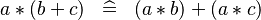 |
M | |
| * | DISTRI_PROD_MINUS | 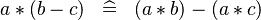 |
M | |
| * | DERIV_LE_CARD | 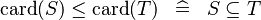 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_GE_CARD | 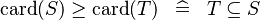 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_LT_CARD | 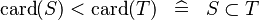 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_GT_CARD | 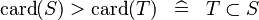 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_EQUAL_CARD | 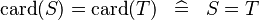 |
 and and  must be of the same type must be of the same type |
M |