Arithmetic Rewrite Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Nicolas m added SIMP_MULTI_MINUS_PLUS_L, SIMP_MULTI_MINUS_PLUS_R, SIMP_MULTI_MINUS_PLUS_PLUS, SIMP_MULTI_PLUS_MINUS |
imported>Nicolas m added SIMP_MULTI_ARITHREL_PLUS_PLUS, SIMP_MULTI_ARITHREL_PLUS_R, SIMP_MULTI_ARITHREL_PLUS_L, SIMP_MULTI_ARITHREL_MINUS_MINUS_R, SIMP_MULTI_ARITHREL_MINUS_MINUS_L |
||
| Line 58: | Line 58: | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_MINUS_PLUS_PLUS}}||<math> (A + \ldots + E + \ldots + B) - (C + \ldots + E + \ldots + D) \;\;\defi\;\; (A + \ldots + B) - (C + \ldots + D) </math>|| || M | {{RRRow}}|*||{{Rulename|SIMP_MULTI_MINUS_PLUS_PLUS}}||<math> (A + \ldots + E + \ldots + B) - (C + \ldots + E + \ldots + D) \;\;\defi\;\; (A + \ldots + B) - (C + \ldots + D) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_PLUS_MINUS}}||<math>(A + \ldots + D + \ldots + (C - D) + \ldots + B) \;\;\defi\;\; A + \ldots + C + \ldots + B </math>|| || M | {{RRRow}}|*||{{Rulename|SIMP_MULTI_PLUS_MINUS}}||<math>(A + \ldots + D + \ldots + (C - D) + \ldots + B) \;\;\defi\;\; A + \ldots + C + \ldots + B </math>|| || M | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_ARITHREL_PLUS_PLUS}}||<math> A + \ldots + E + \ldots + B < C + \ldots + E + \ldots + D \;\;\defi\;\; A + \ldots + B < C + \ldots + D </math>|| where the root relation (<math><</math> here) is one of <math>\{=, <, \leq, >, \geq\}</math>|| M | |||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_ARITHREL_PLUS_R}}||<math> C < A + \ldots + C \ldots + B \;\;\defi\;\; 0 < A + \ldots + B </math>||where the root relation (<math><</math> here) is one of <math>\{=, <, \leq, >, \geq\}</math> || M | |||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_ARITHREL_PLUS_L}}||<math> A + \ldots + C \ldots + B < C \;\;\defi\;\; A + \ldots + B < 0 </math>||where the root relation (<math><</math> here) is one of <math>\{=, <, \leq, >, \geq\}</math> || M | |||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_ARITHREL_MINUS_MINUS_R}}||<math> A - C < B - C \;\;\defi\;\; A < B </math>||where the root relation (<math><</math> here) is one of <math>\{=, <, \leq, >, \geq\}</math> || M | |||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_ARITHREL_MINUS_MINUS_L}}||<math> C - A < C - B \;\;\defi\;\; B < A </math>||where the root relation (<math><</math> here) is one of <math>\{=, <, \leq, >, \geq\}</math> || M | |||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_PROD_0}}||<math> E * \ldots * 0 * \ldots * F \;\;\defi\;\; 0 </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_PROD_0}}||<math> E * \ldots * 0 * \ldots * F \;\;\defi\;\; 0 </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_PROD_1}}||<math> E * \ldots * 1 * \ldots * F \;\;\defi\;\; E * \ldots * F </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_PROD_1}}||<math> E * \ldots * 1 * \ldots * F \;\;\defi\;\; E * \ldots * F </math>|| || A | ||
Revision as of 13:14, 26 August 2009
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
SIMP_SPECIAL_MOD_0 |
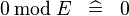 |
A | ||
SIMP_SPECIAL_MOD_1 |
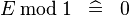 |
A | ||
| * | SIMP_MIN_SING |
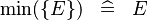 |
where  is a single expression is a single expression |
A |
| * | SIMP_MAX_SING |
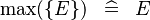 |
where  is a single expression is a single expression |
A |
| * | SIMP_MIN_NATURAL |
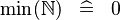 |
A | |
| * | SIMP_MIN_NATURAL1 |
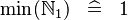 |
A | |
| * | SIMP_MIN_BUNION_SING |
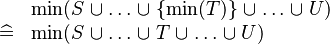 |
A | |
| * | SIMP_MAX_BUNION_SING |
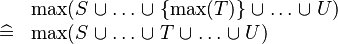 |
A | |
| * | SIMP_MIN_UPTO |
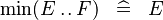 |
A | |
| * | SIMP_MAX_UPTO |
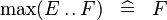 |
A | |
| * | SIMP_LIT_MIN |
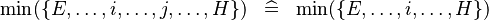 |
where  and and  are literals and are literals and 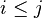 |
A |
| * | SIMP_LIT_MAX |
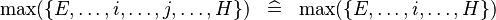 |
where  and and  are literals and are literals and 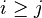 |
A |
| * | SIMP_LIT_MIN_UPTO |
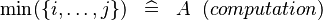 |
where 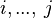 are literals are literals |
A |
| * | SIMP_LIT_MAX_UPTO |
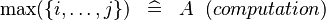 |
where 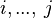 are literals are literals |
A |
| * | SIMP_SPECIAL_CARD |
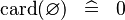 |
A | |
| * | SIMP_CARD_SING |
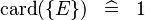 |
where  is a single expression is a single expression |
A |
| * | SIMP_SPECIAL_EQUAL_CARD |
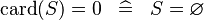 |
A | |
| * | SIMP_CARD_POW |
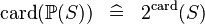 |
A | |
| * | SIMP_CARD_BUNION |
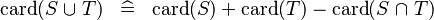 |
A | |
| * | SIMP_CARD_SETMINUS |
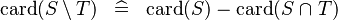 |
A | |
| * | SIMP_CARD_CPROD |
 |
A | |
| * | SIMP_CARD_CONVERSE |
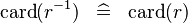 |
A | |
| * | SIMP_CARD_ID |
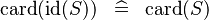 |
A | |
| * | SIMP_CARD_LAMBDA |
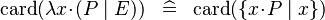 |
A | |
| * | SIMP_CARD_COMPSET |
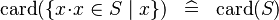 |
where  non free in non free in  |
A |
| * | SIMP_LIT_CARD_UPTO |
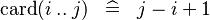 |
where  and and  are literals and are literals and 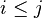 |
A |
| * | SIMP_TYPE_CARD |
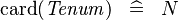 |
where 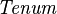 is a carrier set containing is a carrier set containing 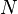 elements elements |
A |
| * | SIMP_LIT_GE_CARD_0 |
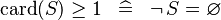 |
A | |
| * | SIMP_LIT_LE_CARD_1 |
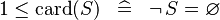 |
A | |
| * | SIMP_LIT_LE_CARD_0 |
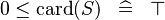 |
A | |
| * | SIMP_LIT_GE_CARD_0 |
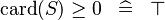 |
A | |
| * | SIMP_LIT_GT_CARD_0 |
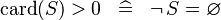 |
A | |
| * | SIMP_LIT_LT_CARD_0 |
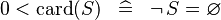 |
A | |
| * | SIMP_LIT_EQUAL_CARD_1 |
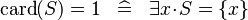 |
A | |
| * | SIMP_CARD_NATURAL |
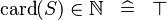 |
A | |
| * | SIMP_CARD_NATURAL1 |
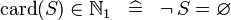 |
A | |
| * | SIMP_LIT_IN_NATURAL |
 |
where  is a literal is a literal |
A |
SIMP_SPECIAL_IN_NATURAL1 |
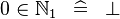 |
A | ||
| * | SIMP_LIT_IN_NATURAL1 |
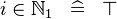 |
where  is a literal and is a literal and 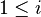 |
A |
| * | SIMP_LIT_UPTO |
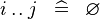 |
where  and and  are literals and are literals and 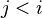 |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL |
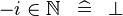 |
where  is a literal and is a literal and 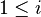 |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL1 |
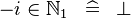 |
where  is a literal is a literal |
A |
SIMP_SPECIAL_KBOOL_BTRUE |
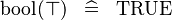 |
A | ||
SIMP_SPECIAL_KBOOL_BFALSE |
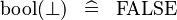 |
A | ||
| * | SIMP_LIT_EQUAL_KBOOL_TRUE |
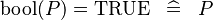 |
A | |
| * | SIMP_LIT_EQUAL_KBOOL_FALSE |
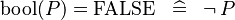 |
A | |
| * | DEF_EQUAL_MIN |
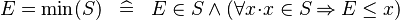 |
where  non free in non free in 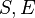 |
M |
| * | DEF_EQUAL_MAX |
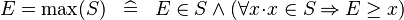 |
where  non free in non free in 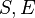 |
M |
| * | SIMP_SPECIAL_PLUS |
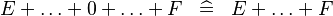 |
A | |
| * | SIMP_SPECIAL_MINUS_R |
 |
A | |
| * | SIMP_SPECIAL_MINUS_L |
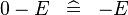 |
A | |
| * | SIMP_MINUS_MINUS |
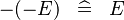 |
A | |
| * | SIMP_MINUS_UNMINUS |
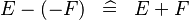 |
where 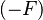 is a unary minus expression or a negative literal is a unary minus expression or a negative literal |
M |
| * | SIMP_MULTI_MINUS |
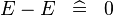 |
A | |
| * | SIMP_MULTI_MINUS_PLUS_L |
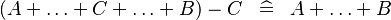 |
M | |
| * | SIMP_MULTI_MINUS_PLUS_R |
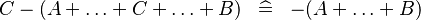 |
M | |
| * | SIMP_MULTI_MINUS_PLUS_PLUS |
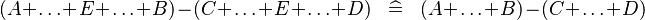 |
M | |
| * | SIMP_MULTI_PLUS_MINUS |
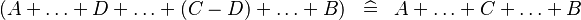 |
M | |
| * | SIMP_MULTI_ARITHREL_PLUS_PLUS |
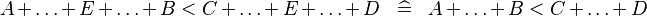 |
where the root relation (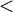 here) is one of here) is one of 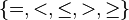 |
M |
| * | SIMP_MULTI_ARITHREL_PLUS_R |
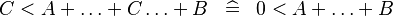 |
where the root relation (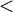 here) is one of here) is one of 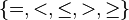 |
M |
| * | SIMP_MULTI_ARITHREL_PLUS_L |
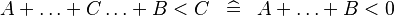 |
where the root relation (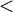 here) is one of here) is one of 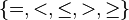 |
M |
| * | SIMP_MULTI_ARITHREL_MINUS_MINUS_R |
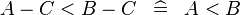 |
where the root relation (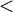 here) is one of here) is one of 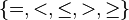 |
M |
| * | SIMP_MULTI_ARITHREL_MINUS_MINUS_L |
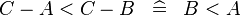 |
where the root relation (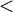 here) is one of here) is one of 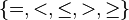 |
M |
| * | SIMP_SPECIAL_PROD_0 |
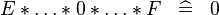 |
A | |
| * | SIMP_SPECIAL_PROD_1 |
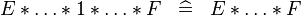 |
A | |
| * | SIMP_SPECIAL_PROD_MINUS_EVEN |
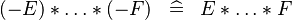 |
if an even number of  |
A |
| * | SIMP_SPECIAL_PROD_MINUS_ODD |
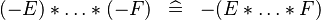 |
if an odd number of  |
A |
| * | SIMP_LIT_MINUS |
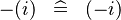 |
where  is a literal is a literal |
A |
| * | SIMP_LIT_MINUS_MINUS |
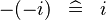 |
where  is a literal is a literal |
A |
| * | SIMP_LIT_EQUAL |
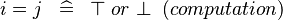 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_LE |
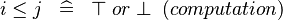 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_LT |
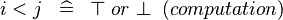 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_GE |
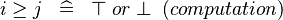 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_GT |
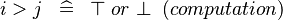 |
where  and and  are literals are literals |
A |
| * | SIMP_DIV_MINUS |
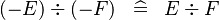 |
A | |
SIMP_SPECIAL_DIV_1 |
 |
A | ||
| * | SIMP_SPECIAL_DIV_0 |
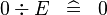 |
A | |
| * | SIMP_SPECIAL_EXPN_1_R |
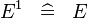 |
A | |
| * | SIMP_SPECIAL_EXPN_1_L |
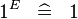 |
A | |
| * | SIMP_SPECIAL_EXPN_0 |
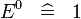 |
A | |
| * | SIMP_MULTI_LE |
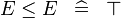 |
A | |
| * | SIMP_MULTI_LT |
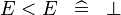 |
A | |
| * | SIMP_MULTI_GE |
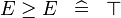 |
A | |
| * | SIMP_MULTI_GT |
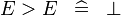 |
A | |
| * | SIMP_MULTI_DIV |
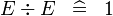 |
A | |
| * | SIMP_MULTI_DIV_PROD |
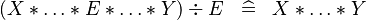 |
A | |
| * | SIMP_MULTI_MOD |
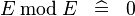 |
A | |
| * | DISTRI_PROD_PLUS |
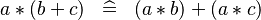 |
M | |
| * | DISTRI_PROD_MINUS |
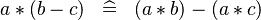 |
M | |
| * | DERIV_LE_CARD |
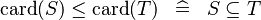 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_GE_CARD |
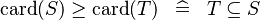 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_LT_CARD |
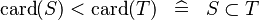 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_GT_CARD |
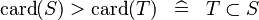 |
 and and  must be of the same type must be of the same type |
M |
| * | DERIV_EQUAL_CARD |
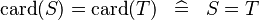 |
 and and  must be of the same type must be of the same type |
M |
DERIV_NOT_EQUAL |
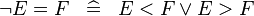 |
 and and 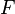 must be of Integer type must be of Integer type |
M |