Rodin Proof Tactics

This page contains descriptions of the available proof tactics within the RODIN Platform.

For each tactic, the descriptions is as follows:

• Description: A high-level description of the tactic. This will be the description appeared in the RODIN Platform preferences.

• Additional details: (Optional) Details explanation of the tactic.

• ID: An unique ID associated with the tactic.

• Auto-tactic: No: the tactic cannot be added as an auto-tactic. Yes: the tactic can be added as an auto-tactic. Default: the tactic is a default auto-tactic.

• Post-tactic: No: the tactic cannot be added as a post-tactic. Yes: the tactic can be added as a post-tactic. Default: the tactic is a default post-tactic.

• Preference display: Information on how an application of the tactic is displayed in the auto-tactic preference or the post-tactic preference.

• Interactive: No: the tactic cannot be invoked interactively. Global: The tactic can be invoked from the Proof Control. Goal: The tactic can be invoked from the goal view. Hypothesis: The tactic can be invoked from the hypothesis view. If the tactic can be invoked interactively (i.e. either Global, Goal or Hypothesis), more information about how this could be done will be given. Note that since the Post-tactics can be launched manually, any tactics that can be included in the post-tactic in principle can be invoked interactively via the post-tactic. Here No only means that there is no separate invocation for this specific tactic.

• Proving interface display: Example(s) on how an application of this tactic can be seen from the proving interface of the RODIN Platform.

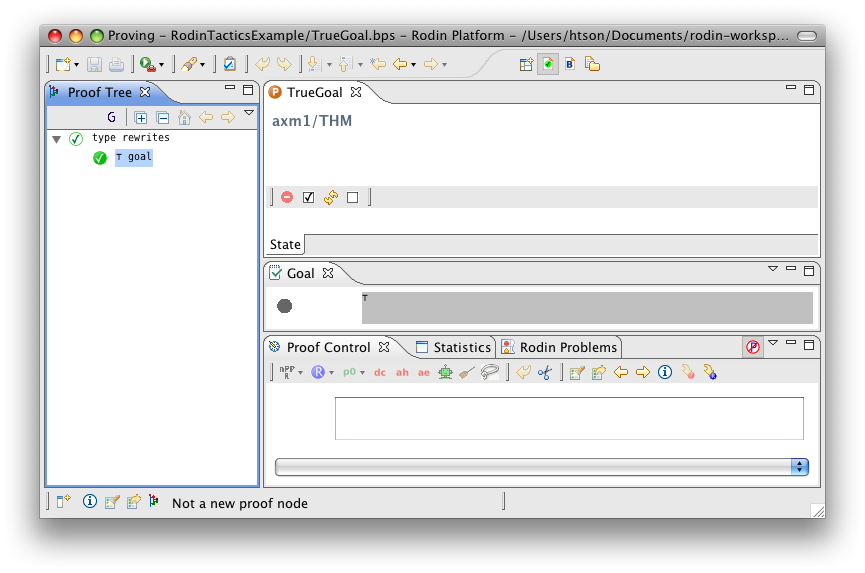
True Goal

• Description: Discharges any sequent whose goal is '⊤' (logical true).

• ID: org.eventb.core.seqprover.trueGoalTac

• Auto-tactic: Default

• Post-tactic: Default

• Preference display: True Goal (Discharge)

• Interactive: No

• Proving interface display: ⊤ goal

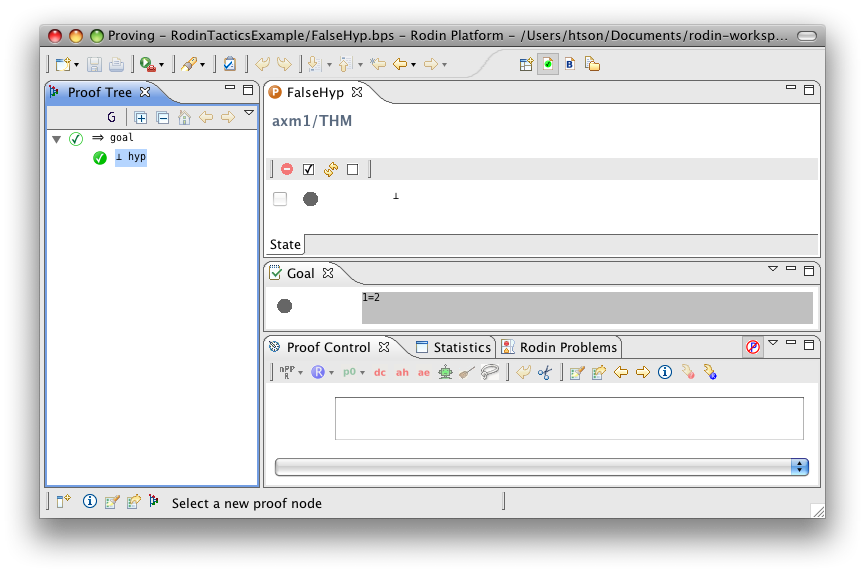
False Hypothesis

• Description: Discharges any sequent containing a '⊥' hypothesis

• ID: org.eventb.core.seqprover.falseHypTac

• Auto-tactic: Default

• Post-tactic: Default

• Preference display: False Hypothesis (Discharge)

• Interactive: No

• Proving interface display: ⊥ hyp

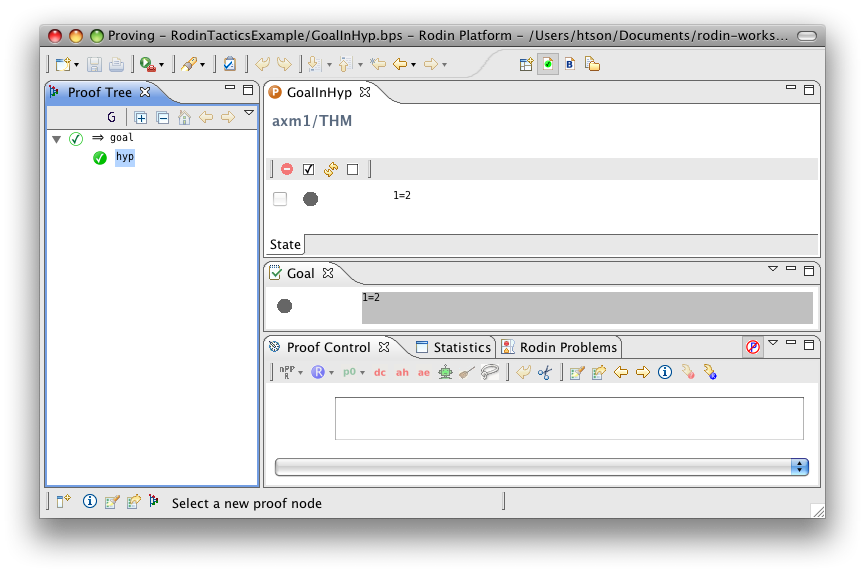
Goal in Hypotheses

• Description: Discharges any sequent whose goal is contained in its hypotheses

• ID: org.eventb.core.seqprover.goalInHypTac

• Auto-tactic: Default

• Post-tactic: Default

• Preference display: Goal in Hypotheses (Discharge)

• Interactive: No

• Proving interface display: hyp

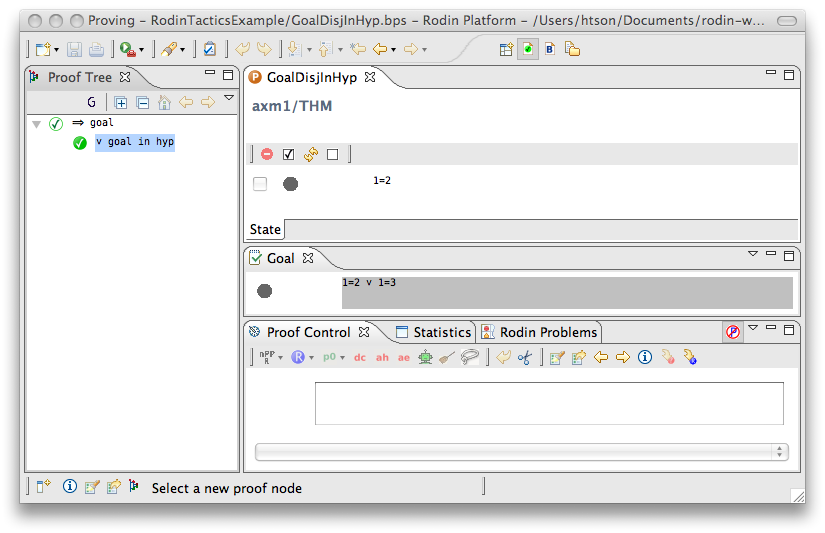
Goal Disjunct in Hypothesis

• Description: Discharges any sequent whose goal is a disjunction and one of whose disjuncts is present in the hypotheses.

• ID: org.eventb.core.seqprover.goalDisjInHypTac

• Auto-tactic: No

• Post-tactic: Default

• Preference display: Goal Disjunct in Hypotheses (Discharge)

• Interactive: No

• Proving interface display: ∨ goal in hyp

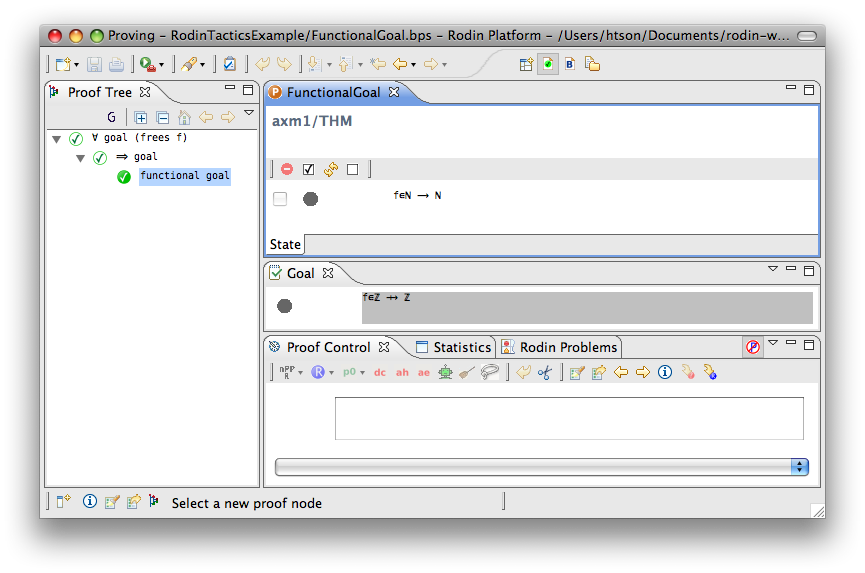
Functional Goal

• Description: Tries to discharge a sequent whose goal states that an expression is a function (i.e. f ∈ T1 ⇸ T2, where T1 and T2 are type expressions).

• Additional details: The sequent is discharged if there is a hypothesis specifying that f is a function of any kind (i.e. partial function, total function, partial injection, total injection, partial surjection, total surjection, bijection).

• ID: org.eventb.core.seqprover.funGoalTac

• Auto-tactic: Default

• Post-tactic: Default

• Preference display: Functional Goal (Discharge)

• Interactive: No

• Proving interface display: functional goal

Simplification Rewriter

• Description: Tries to simplify all predicates in a sequent using pre-defined simplification rewriting rules.

• Additional details: The list of rewriting rules are in the following page http://wiki.event-b.org/index.php/All_Rewrite_Rules, which are marked as Automatic.

• ID: org.eventb.core.seqprover.autoRewriteTac

• Auto-tactic: Default

• Post-tactic: Default

• Preference display: Simplification Rewriter (Simplify)

• Interactive: No

• Proving interface display: simplification rewrites

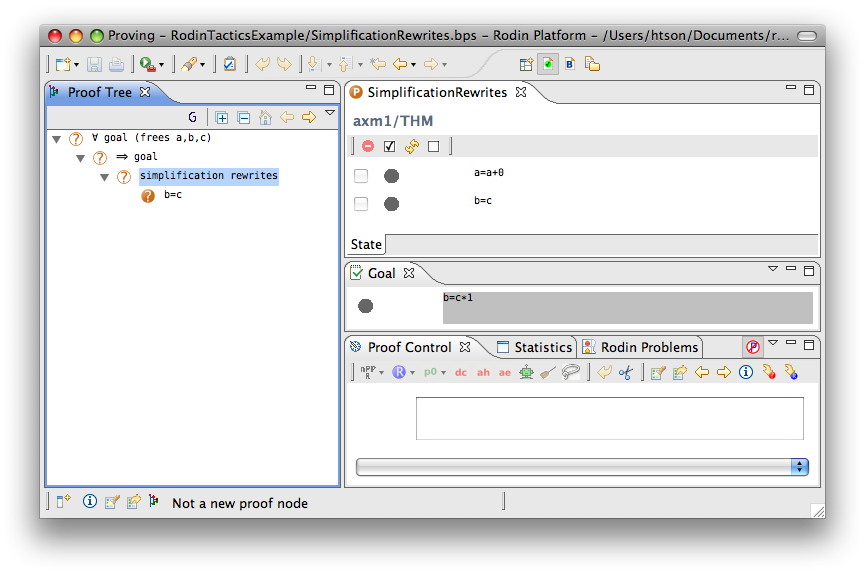
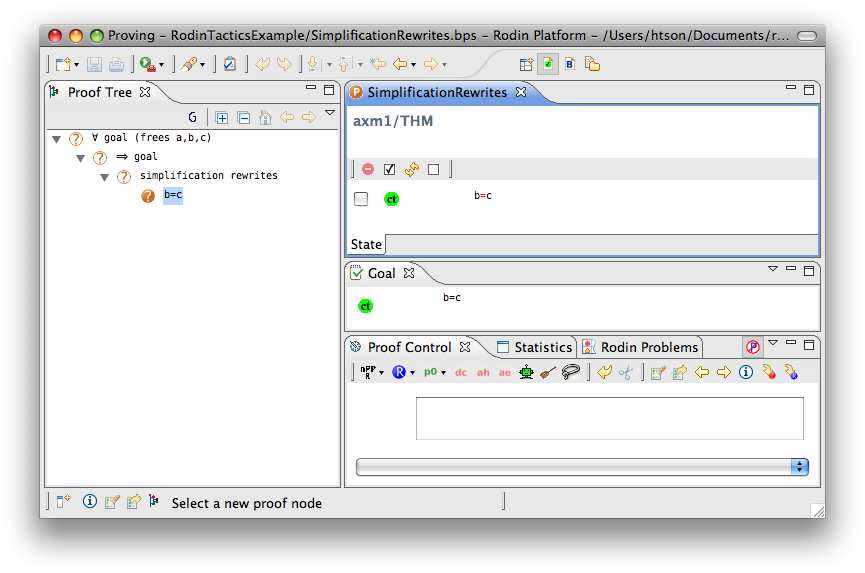
The example below shows the screen-shot of the step before the application of the tactic and the step just after the application of the tactic. There are 3 rewritings have been done as follows.

$\begin{array}{rcl} a + 0 & \Longrightarrow & a \\ a = a & \Longrightarrow & \btrue \\ c * 1 & \Longrightarrow & c \\ \end{array}$

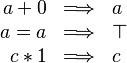
Note that 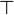$\btrue$ hypothesis is always dropped in the RODIN Platform.

Before

After

Type Rewriter

• Description: Simplifies predicates containing type expressions such as E ∈ T to ⊤ and T = ∅ to ⊥.

• Additional details: More information about type expressions in Event-B.

• ID: org.eventb.core.seqprover.typeRewriteTac

• Auto-tactic: Default

• Post-tactic: Default

• Preference display: Type Rewriter (Simplify)

• Interactive: No

• Proving interface display:

Implication Goal

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

For-all Goal

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Exists Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Find Contradictory Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Use Equality Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Shrink Implicative Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Shrink Enumerated Set

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Implicative Hypothesis with Conjunctive RHS

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Implicative Hypothesis with Disjunctive LHS

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Conjunctive Goal

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Clarify Goal

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Functional Overriding in Goal

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Functional Overriding in Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Partition Rewriter

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

One-Point Rule in Goal

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

One-Point Rule in Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO

Bounded Goal with Finite Hypothesis

• Description: TODO

• ID: TODO

• Display: TODO

• Auto-tactic: TODO

• Post-tactic: TODO

• Interactive: TODO

• Example: TODO