Rodin Proof Tactics: Difference between revisions
imported>Son |
imported>Son |
||
| Line 290: | Line 290: | ||
After the second application [[Image:UseEqualityHypExp3.png]] | After the second application [[Image:UseEqualityHypExp3.png]] | ||
== Use Equality Hypothesis from Left to Right == | |||
== Shrink Implicative Hypothesis == | == Shrink Implicative Hypothesis == | ||
Revision as of 11:29, 10 March 2010
This page contains descriptions of the available proof tactics within the RODIN Platform.
For each tactic, the descriptions is as follows:
- Description: A high-level description of the tactic. This will be the description appeared in the RODIN Platform preferences.
- Additional details: (Optional) Details explanation of the tactic.
- ID: An unique ID associated with the tactic.
- Auto-tactic: No: the tactic cannot be added as an auto-tactic. Yes: the tactic can be added as an auto-tactic. Default: the tactic is a default auto-tactic.
- Post-tactic: No: the tactic cannot be added as a post-tactic. Yes: the tactic can be added as a post-tactic. Default: the tactic is a default post-tactic.
- Preference display: Information on how an application of the tactic is displayed in the auto-tactic preference or the post-tactic preference.
- Interactive: No: the tactic cannot be invoked interactively. Global: The tactic can be invoked from the Proof Control. Goal: The tactic can be invoked from the goal view. Hypothesis: The tactic can be invoked from the hypothesis view. If the tactic can be invoked interactively (i.e. either Global, Goal or Hypothesis), more information about how this could be done will be given. Note that since the Post-tactics can be launched manually, any tactics that can be included in the post-tactic in principle can be invoked interactively via the post-tactic. Here No only means that there is no separate invocation for this specific tactic.
- Proving interface display: Example(s) on how an application of this tactic can be seen from the proving interface of the RODIN Platform.
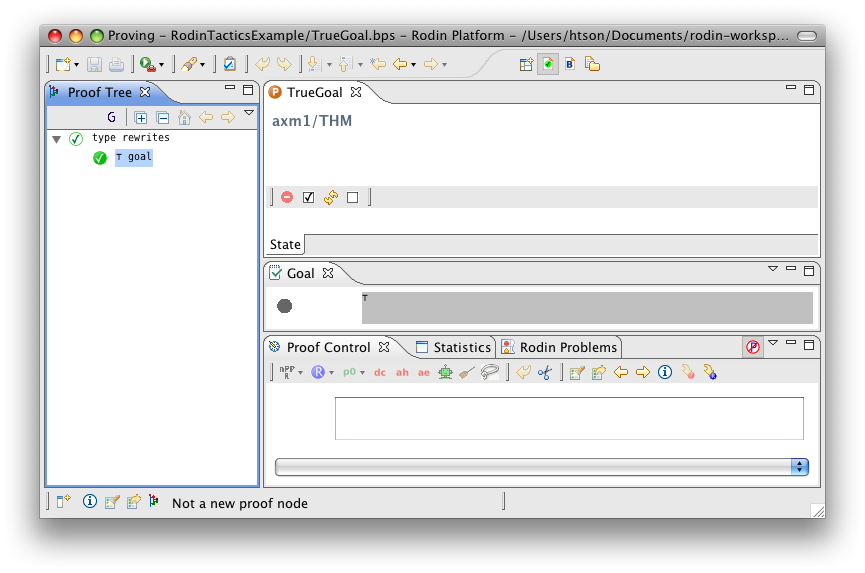
True Goal
- Description: Discharges any sequent whose goal is '⊤' (logical true).
- ID: org.eventb.core.seqprover.trueGoalTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: True Goal (Discharge)
- Interactive: No
- Proving interface display: ⊤ goal
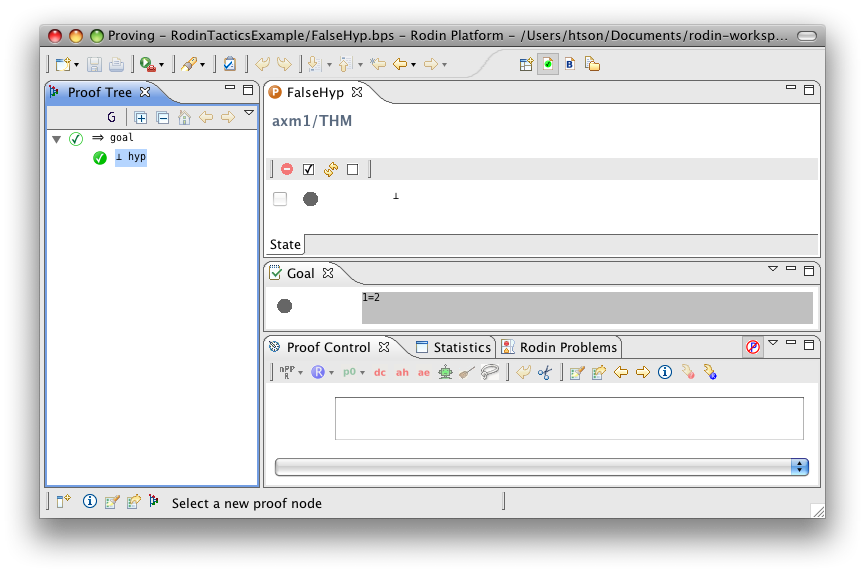
False Hypothesis
- Description: Discharges any sequent containing a '⊥' hypothesis
- ID: org.eventb.core.seqprover.falseHypTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: False Hypothesis (Discharge)
- Interactive: No
- Proving interface display: ⊥ hyp
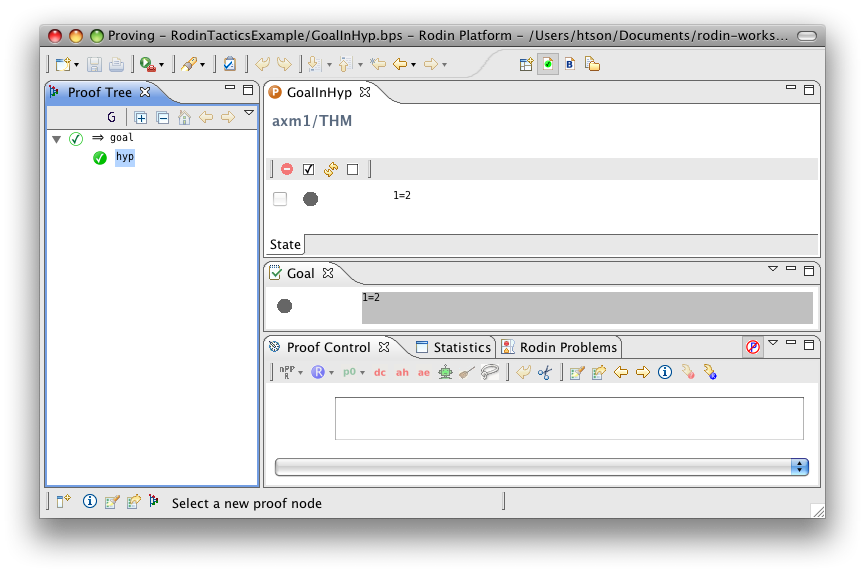
Goal in Hypotheses
- Description: Discharges any sequent whose goal is contained in its hypotheses
- ID: org.eventb.core.seqprover.goalInHypTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Goal in Hypotheses (Discharge)
- Interactive: No
- Proving interface display: hyp
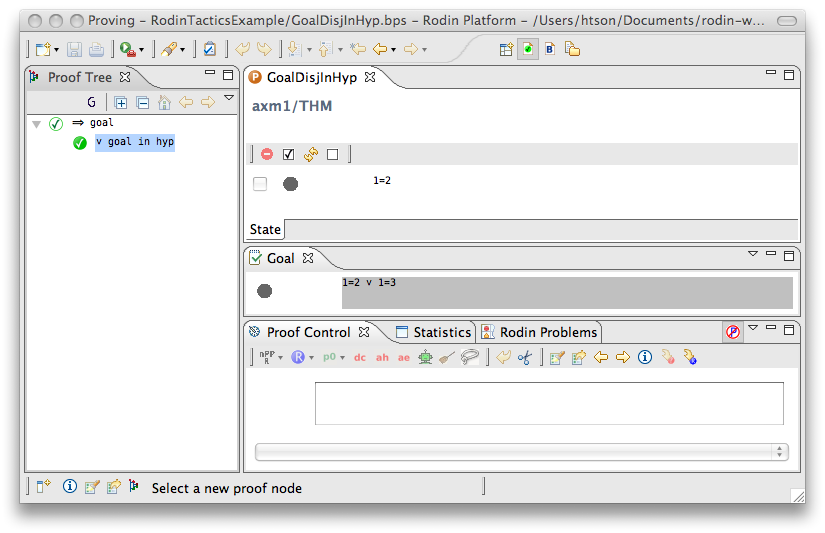
Goal Disjunct in Hypothesis
- Description: Discharges any sequent whose goal is a disjunction and one of whose disjuncts is present in the hypotheses.
- ID: org.eventb.core.seqprover.goalDisjInHypTac
- Auto-tactic: No
- Post-tactic: Default
- Preference display: Goal Disjunct in Hypotheses (Discharge)
- Interactive: No
- Proving interface display: ∨ goal in hyp
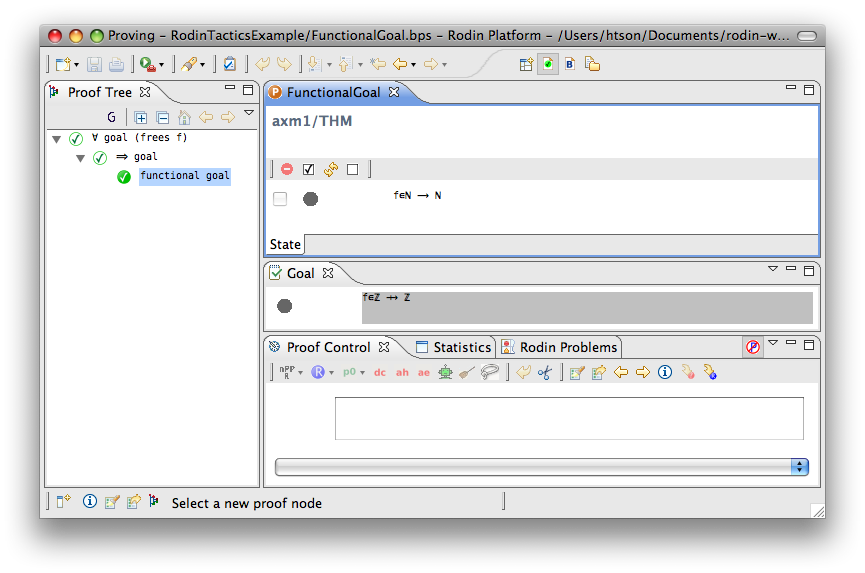
Functional Goal
- Description: Tries to discharge a sequent whose goal states that an expression is a function (i.e. f ∈ T1 ⇸ T2, where T1 and T2 are type expressions).
- Additional details: The sequent is discharged if there is a hypothesis specifying that f is a function of any kind (i.e. partial function, total function, partial injection, total injection, partial surjection, total surjection, bijection). More information about type expressions in Event-B is in the FAQ page.
- ID: org.eventb.core.seqprover.funGoalTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Functional Goal (Discharge)
- Interactive: No
- Proving interface display: functional goal
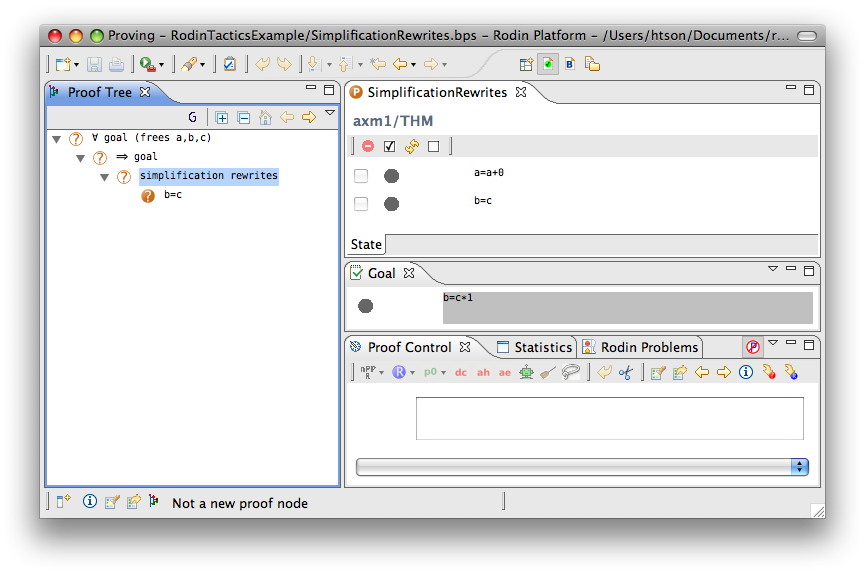
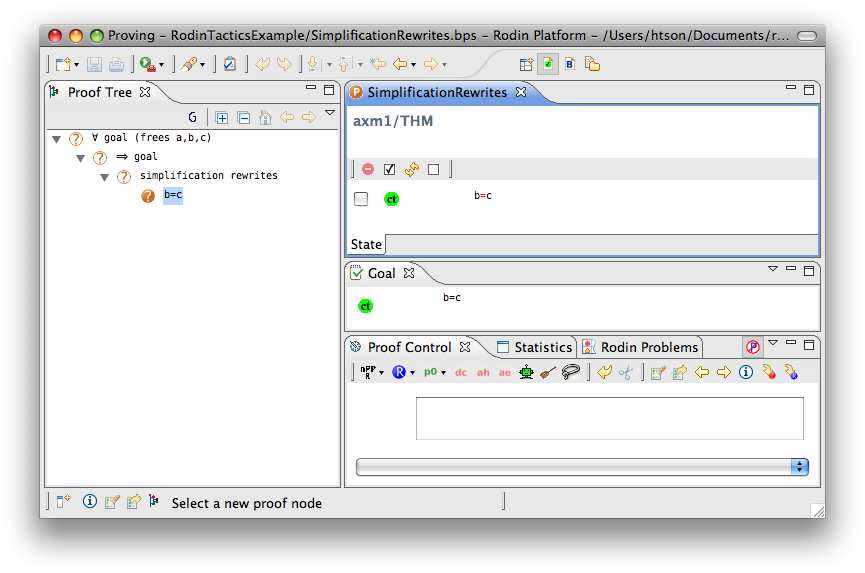
Simplification Rewriter
- Description: Tries to simplify all predicates in a sequent using pre-defined simplification rewriting rules.
- Additional details: The list of rewriting rules are in the following page http://wiki.event-b.org/index.php/All_Rewrite_Rules, which are marked as Automatic.
- ID: org.eventb.core.seqprover.autoRewriteTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Simplification Rewriter (Simplify)
- Interactive: No
- Proving interface display: simplification rewrites
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. There are 3 rewritings have been done as follows.
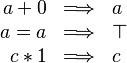
Note that  hypothesis is always dropped in the RODIN Platform.
hypothesis is always dropped in the RODIN Platform.
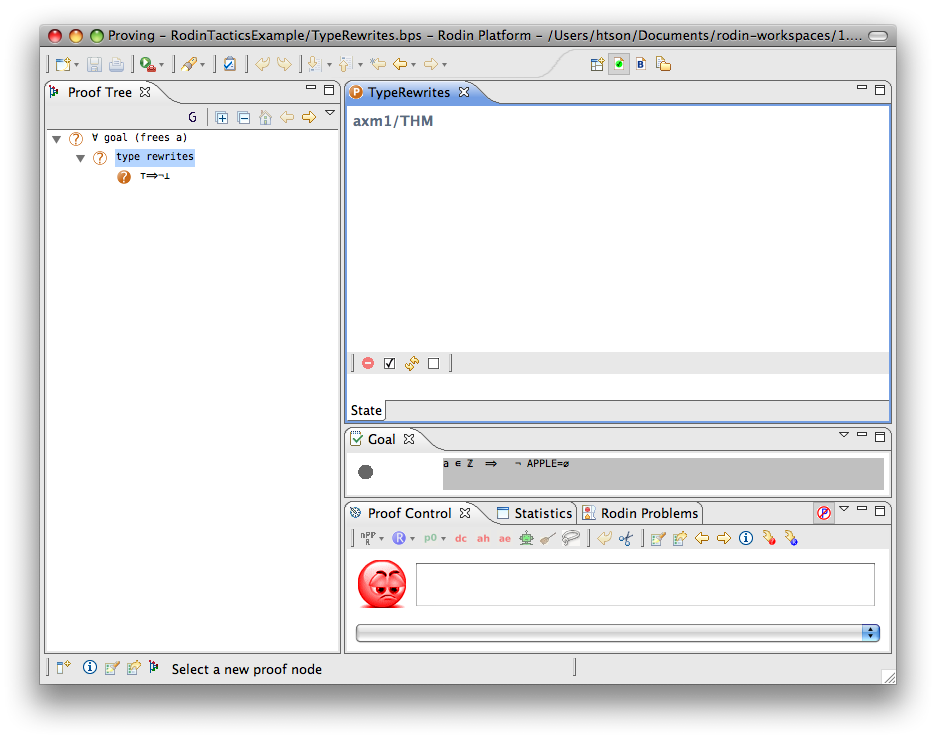
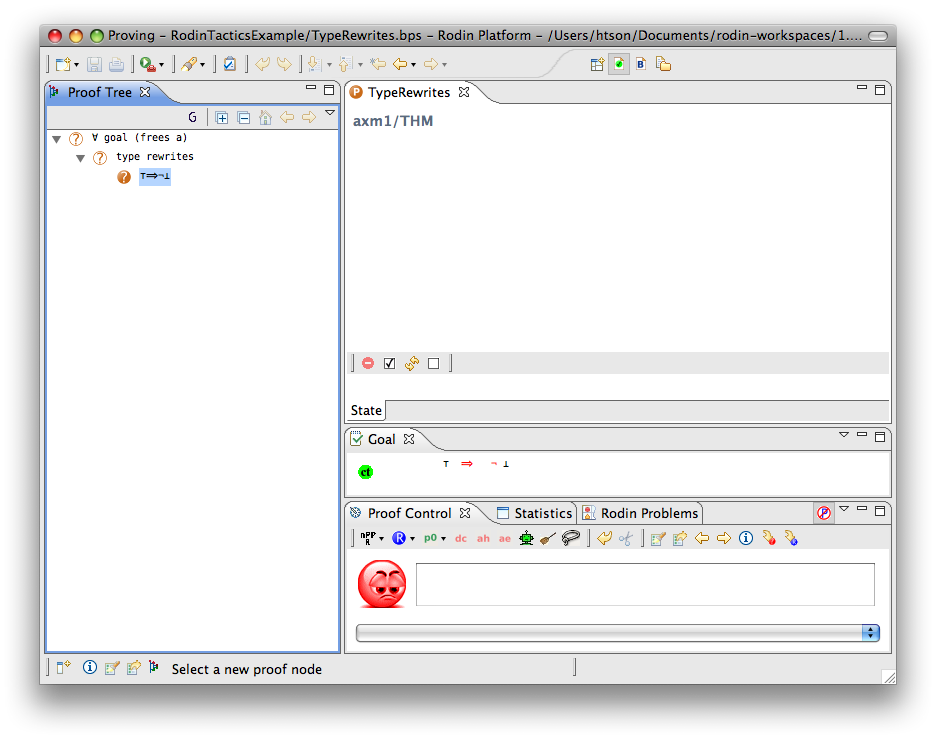
Type Rewriter
- Description: Simplifies predicates containing type expressions such as E ∈ T to ⊤ and T = ∅ to ⊥.
- Additional details: More information about type expressions in Event-B is in the FAQ page.
- ID: org.eventb.core.seqprover.typeRewriteTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Type Rewriter (Simplify)
- Interactive: No
- Proving interface display: type rewrites
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic.
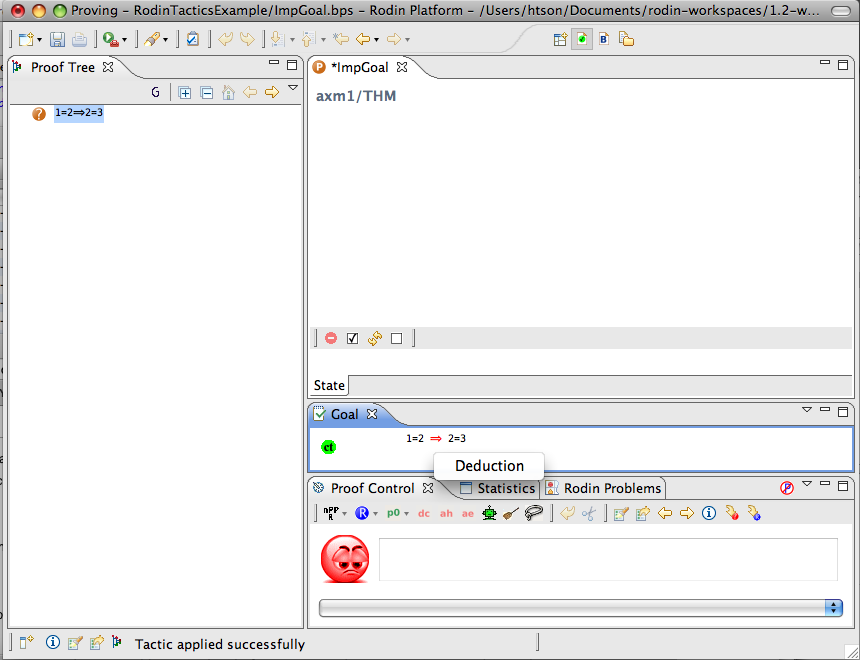
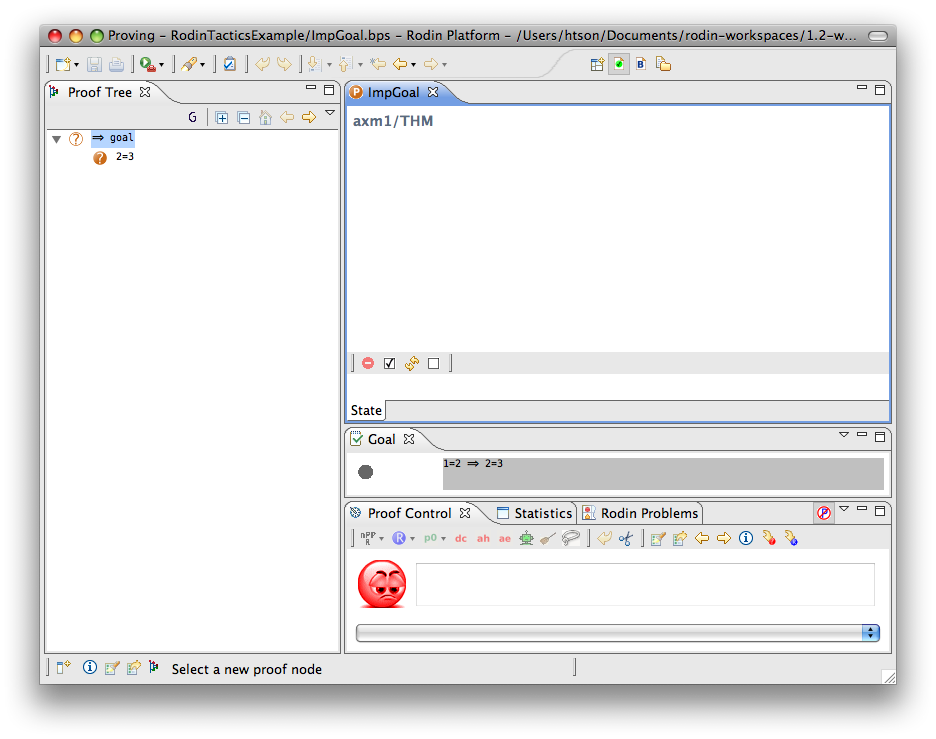
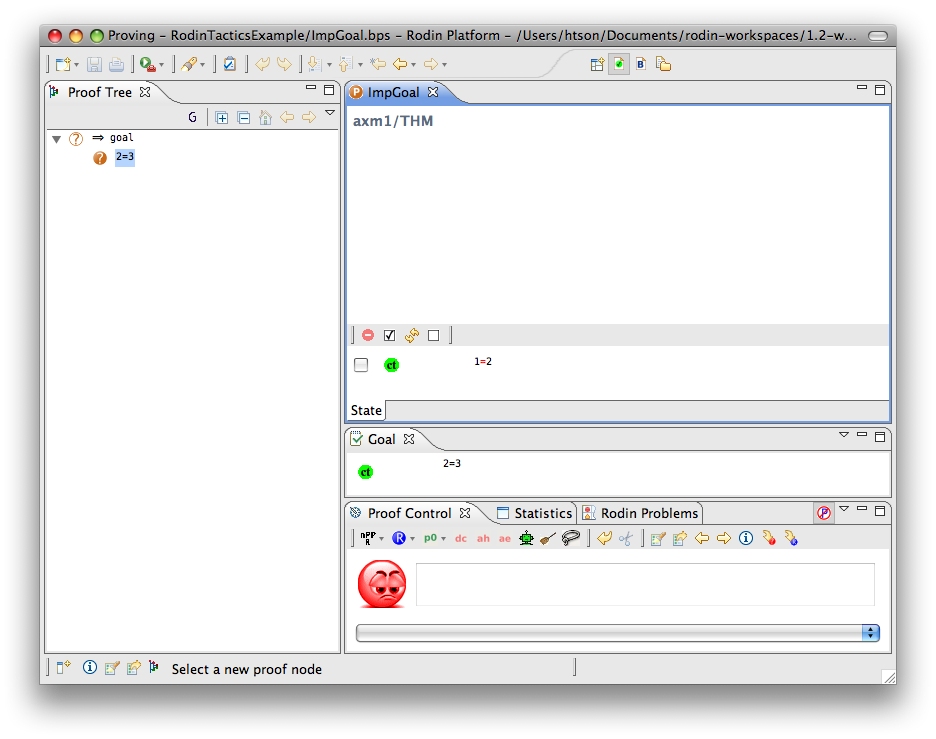
Implication Goal
- Description: Simplifies any sequent with an implicative goal by adding the left hand side of the implication to the hypotheses and making its right hand side the new goal.
- ID: org.eventb.core.seqprover.impGoalTac
- Auto-tactic: No
- Post-tactic: Default
- Preference display: Implicative Goal (Simplify)
- Interactive: Goal. The
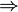 symbol in the implicative goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Deduction.
symbol in the implicative goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Deduction.
- Proving interface display: ⇒ goal
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic.
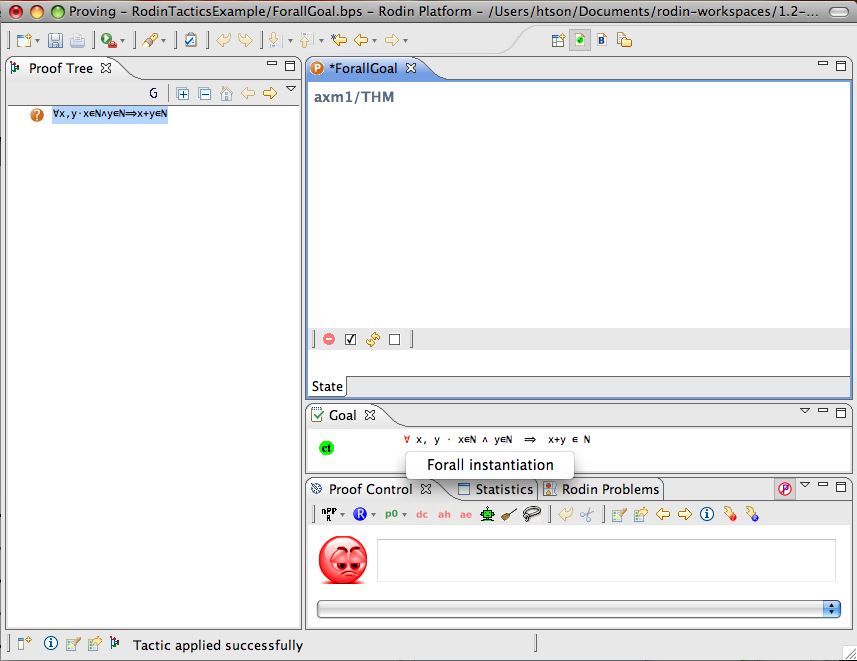
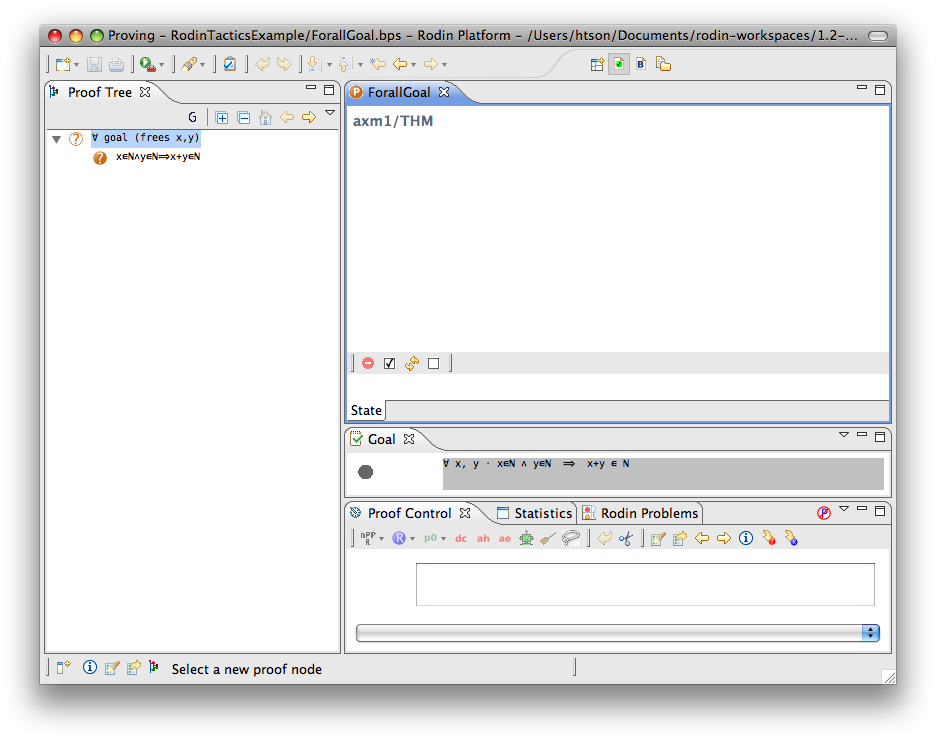
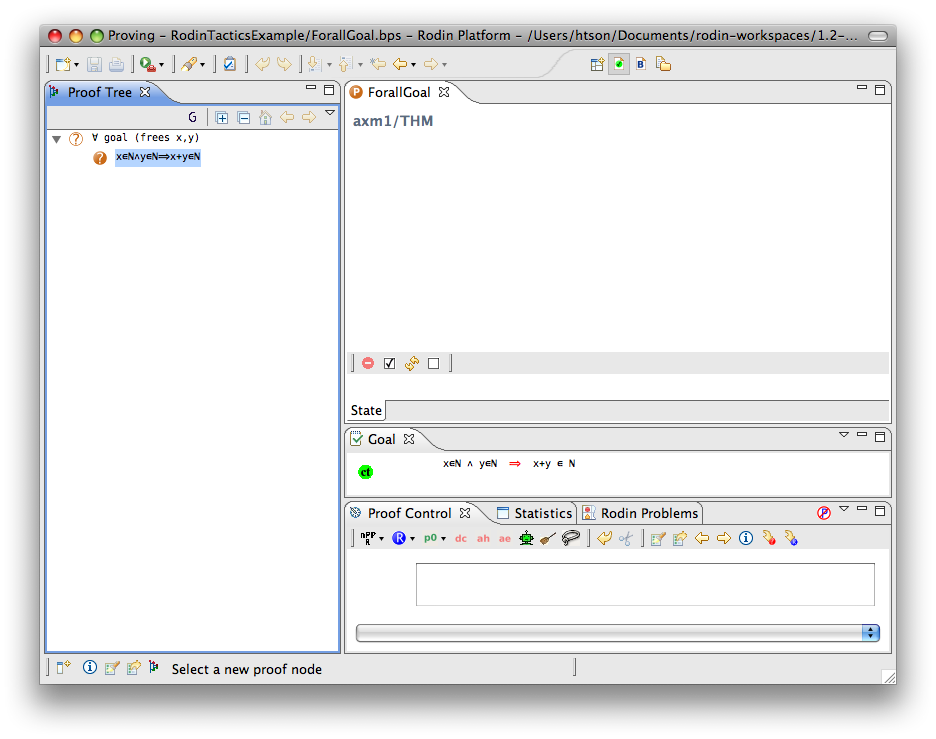
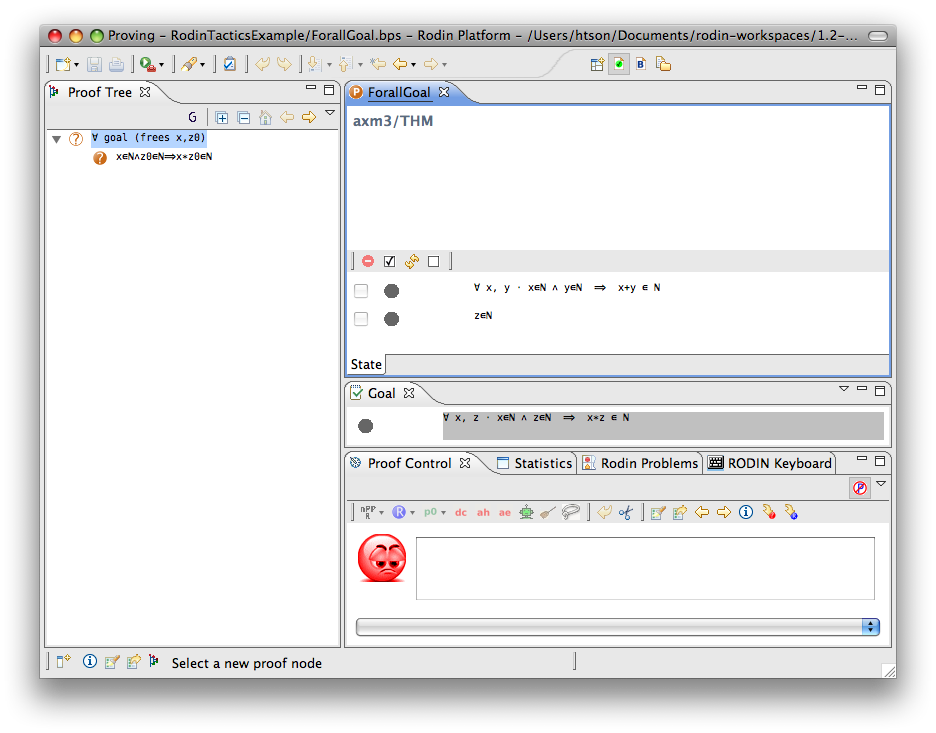
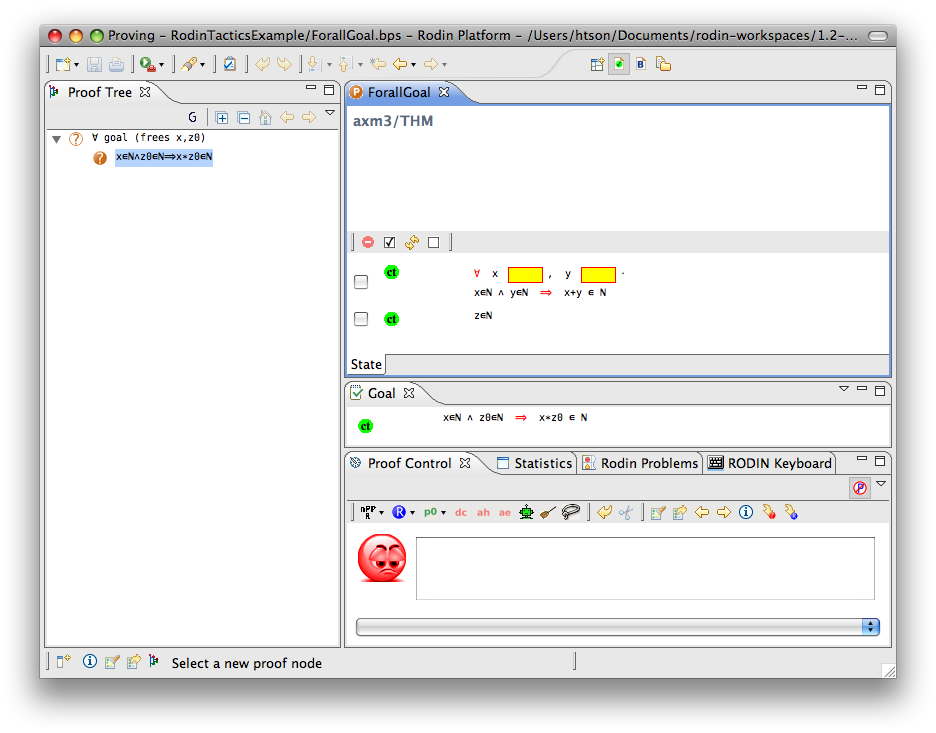
For-all Goal
- Description: Simplifies any sequent with a universally quantified goal by freeing all its bound variables.
- Additional details: The bound variables will be renaming accordingly to avoid name collision.
- ID: org.eventb.core.seqprover.forallGoalTac
- Auto-tactic: No
- Post-tactic: Yes
- Preference display: For-all Goal (Simplify)
- Interactive: Goal. The symbol
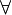 in the universal quantified goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Forall instantiation.
in the universal quantified goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Forall instantiation.
- Proving interface display: ∀ goal (frees list-of-bounded-identifiers)
The first example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. There is no renaming of the bound variable.
The second example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. The bound variable 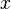 is not renamed, but the bound variable
is not renamed, but the bound variable 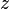 is renamed to
is renamed to 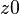 to avoid capture of the existing variable
to avoid capture of the existing variable 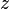 .
.
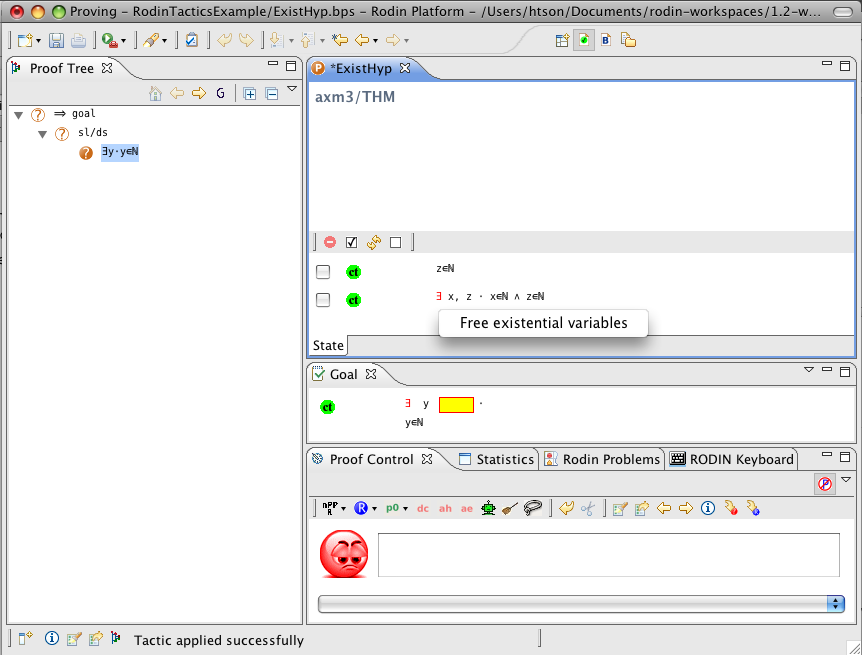
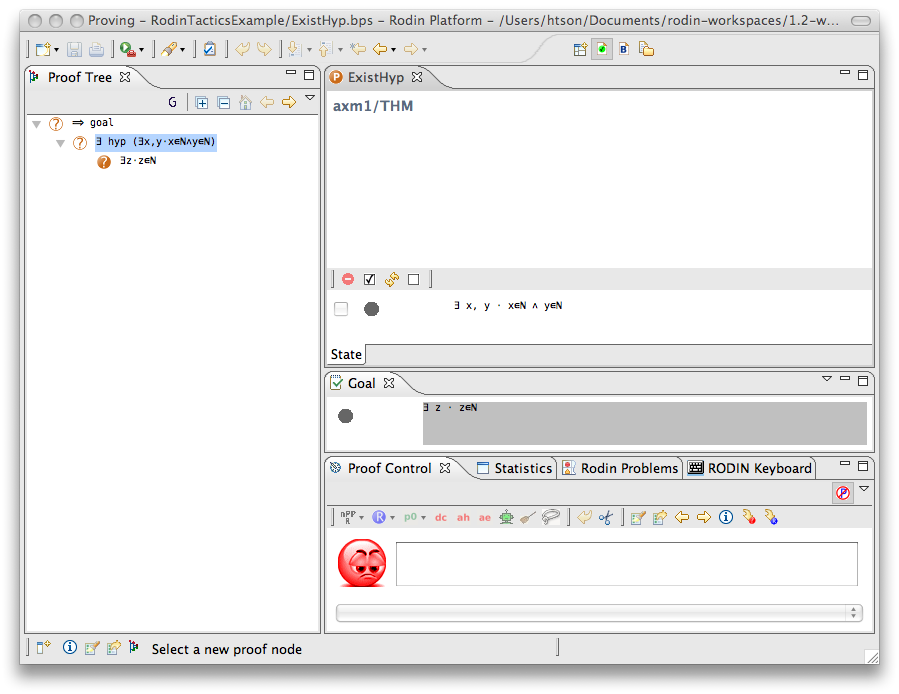
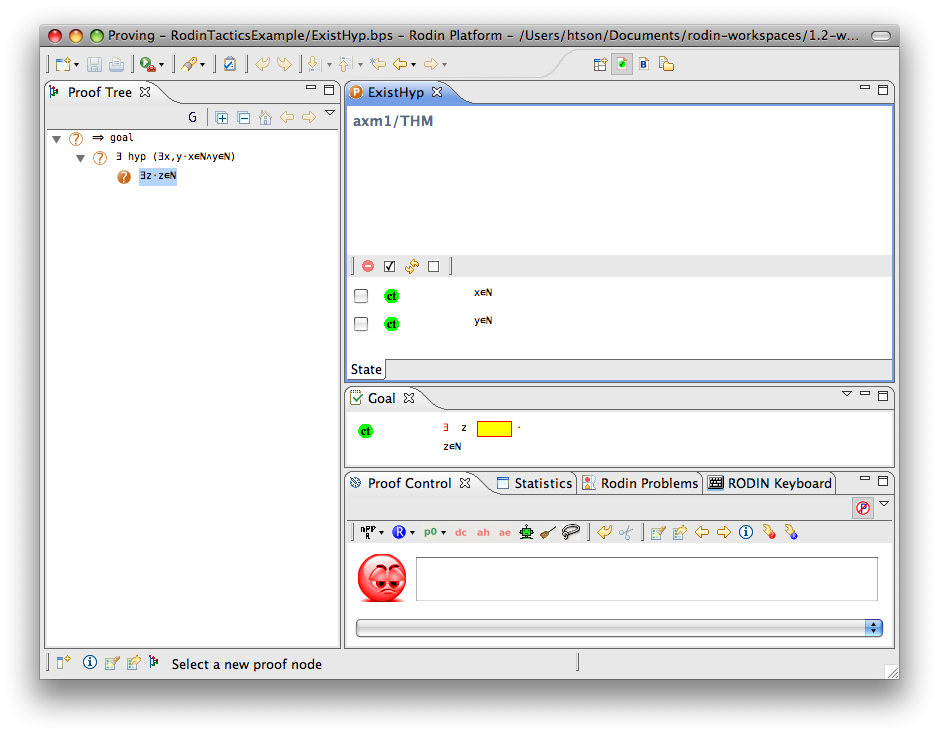
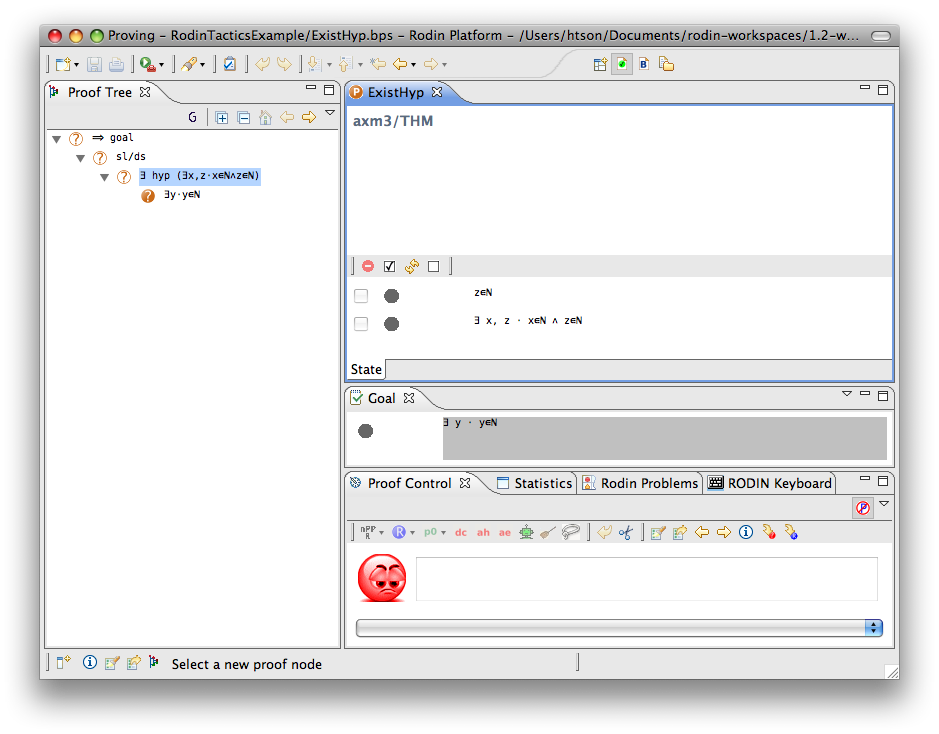
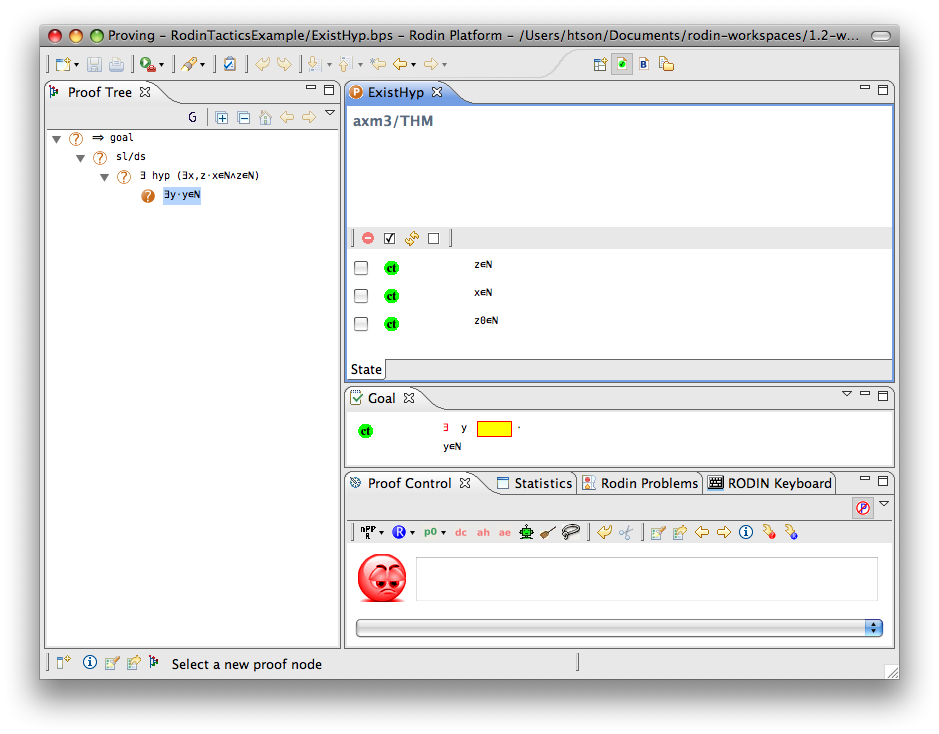
Exists Hypothesis
- Description: In automatic mode (as an auto-tactic or post-tactic), this tactic simplifies any sequent containing existentially quantified hypotheses by freeing their bound variables. In interactive mode, only the selected hypothesis is simplified by freeing its bound variables.
- Additional details: The bound variables will be renaming if necessary to avoid name collision. After freeing their bound variables, if the resulting predicate is a conjunction then it is split into several hypotheses.
- ID: org.eventb.core.seqprover.existHypTac
- Auto-tactic: No
- Post-tactic: Default
- Preference display: Exists Hypotheses (Simplify)
- Interactive: Hypothesis. The symbol
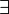 in the existential quantified hypothesis is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Free existential variables.
in the existential quantified hypothesis is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Free existential variables.
- Proving interface display:
The first example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. There is no renaming of the bound variable.
The second example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. The bound variable x is not renamed, but the bound variable z is renamed to z0 to avoid capture of the existing variable z.
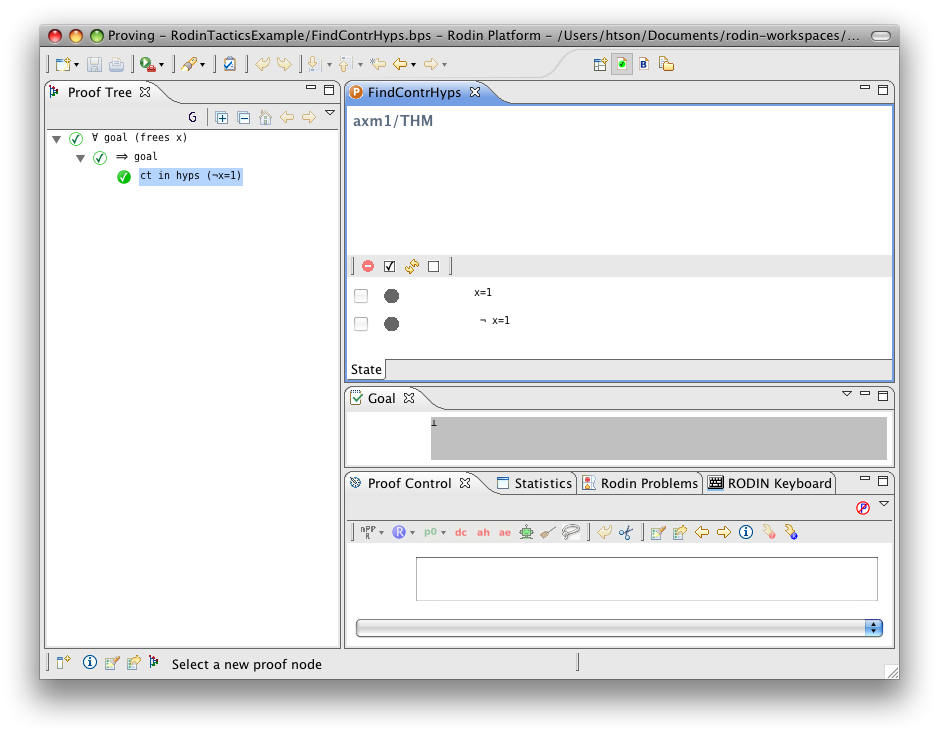
Find Contradictory Hypothesis
- Description: Discharges a sequent by finding contradictory hypotheses, i.e.
 and
and 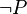 .
.
- Additional details: This tactic tries to find a contradiction using each selected hypothesis that is a negation.
- ID: org.eventb.core.seqprover.findContrHypsTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Find Contradictory Hypotheses (Discharge)
- Interactive: No
- Proving interface display: ct in hyps (the negated hypothesis)
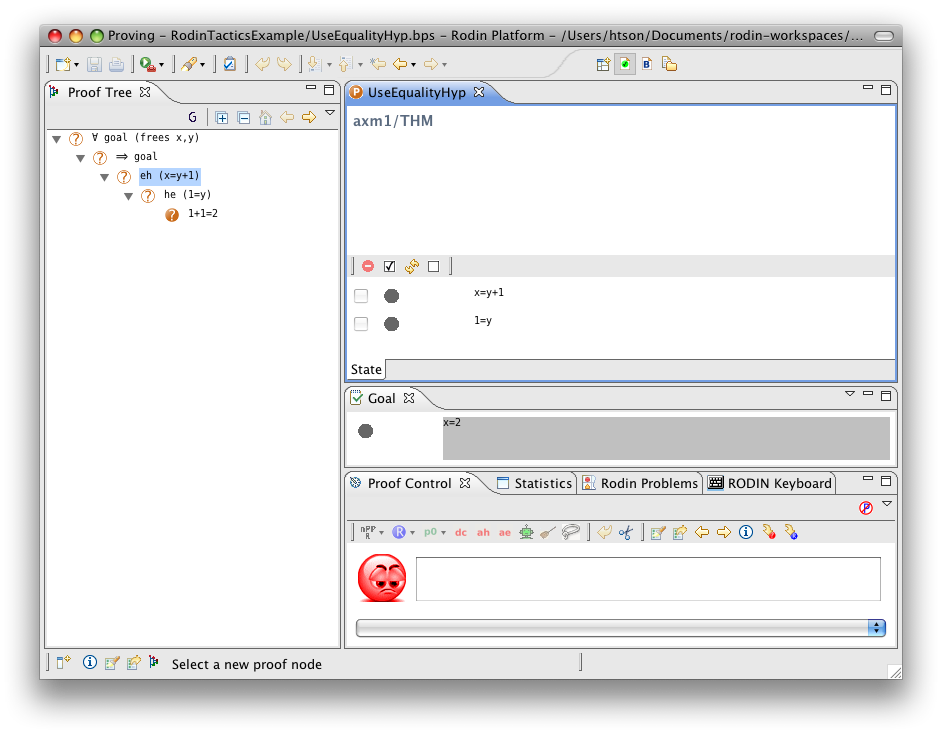
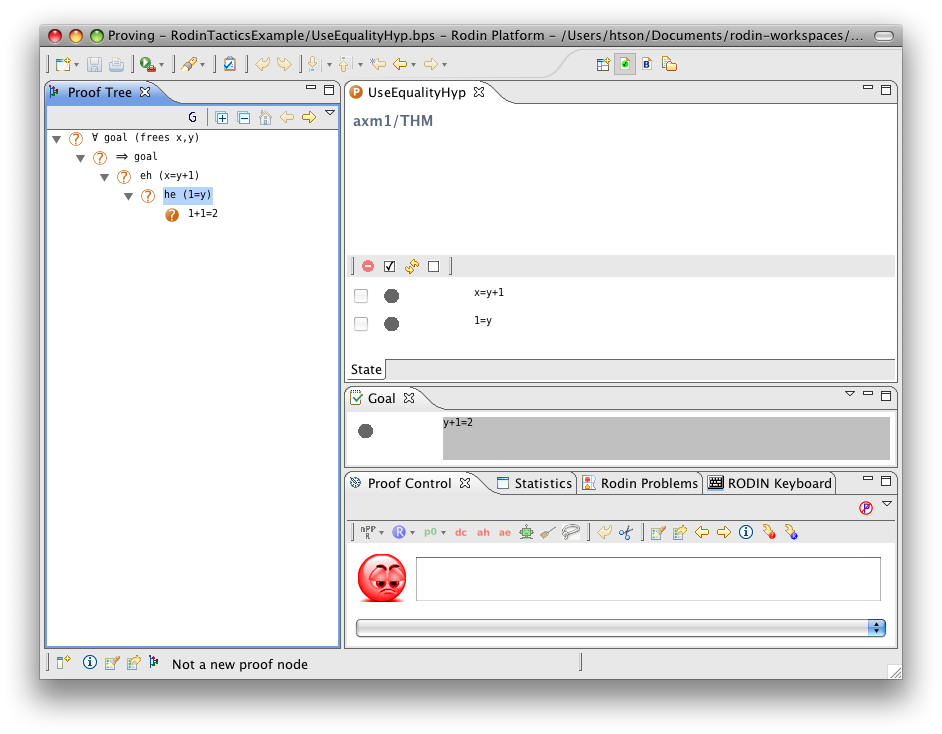
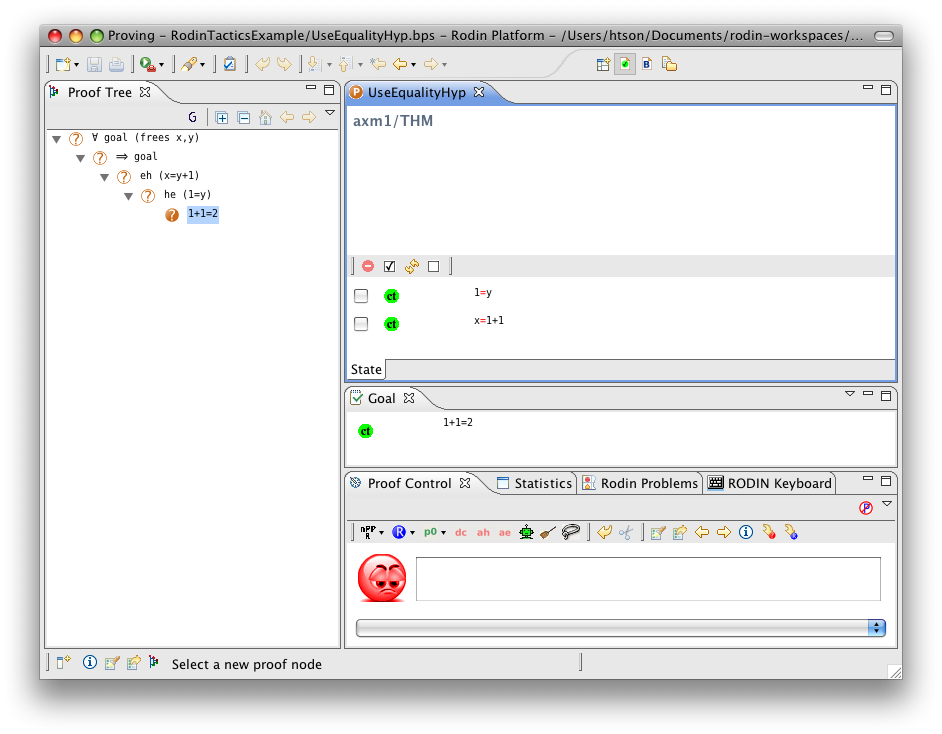
Use Equality Hypothesis
- Description: Simplifies a sequent by rewriting all selected hypotheses and the goal using a (selected) hypothesis that is an equality between a free variable and an expression that does not contain the free variable. The used equality remains in the selected hypotheses to be used again.
- Additional details: Each application of the tactic take only one equality hypothesis into account. If there are several equality hypotheses, they require several applications of the tactic. Moreover, in the case where there are several equality hypotheses, the choice of which hypothesis will be chosen is non-deterministic. This tactic behaves as #Use Equality Hypothesis from Left to Right or #Use Equality Hypothesis from Right to Left depending on if the free variable is on the left or on the right of the equality.
- ID: org.eventb.core.seqprover.eqHypTac
- Auto-tactic: Default
- Post-tactic: Default
- 'Preference display: Use Equals Hypotheses (Simplify)
- Interactive: Hypothesis. See #Use Equality Hypothesis from Left to Right and #Use Equality Hypothesis from Right to Left
- Proving interface display: eh (the equal hypothesis) in the case where the free variable is on the left-hand side or he (the equal hypothesis) in the case where the free variable is on the right-hand side.
The example below shows the screen-shots of the step before the application of the tactic, the step after the first application of the tactic with hypothesis  and the step just after the second application of the tactic with hypothesis
and the step just after the second application of the tactic with hypothesis 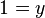 .
.
Use Equality Hypothesis from Left to Right
Shrink Implicative Hypothesis
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Shrink Enumerated Set
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Implicative Hypothesis with Conjunctive RHS
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Implicative Hypothesis with Disjunctive LHS
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Conjunctive Goal
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Clarify Goal
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Functional Overriding in Goal
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Functional Overriding in Hypothesis
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Partition Rewriter
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
One-Point Rule in Goal
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
One-Point Rule in Hypothesis
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO
Bounded Goal with Finite Hypothesis
- Description: TODO
- ID: TODO
- Display: TODO
- Auto-tactic: TODO
- Post-tactic: TODO
- Interactive: TODO
- Example: TODO