Set Rewrite Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Nicolas m updated rule SIMP_FINITE_ID to math V2 |
imported>Tommy m removed * on unimplemented rules |
||
| Line 2: | Line 2: | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_AND_BTRUE}}||<math> P \land \ldots \land \btrue \land \ldots \land Q \;\;\defi\;\; P \land \ldots \land Q </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_AND_BTRUE}}||<math> P \land \ldots \land \btrue \land \ldots \land Q \;\;\defi\;\; P \land \ldots \land Q </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_AND_BFALSE}}||<math> P \land \ldots \land \bfalse \land \ldots \land Q \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_AND_BFALSE}}||<math> P \land \ldots \land \bfalse \land \ldots \land Q \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_AND}}||<math> P \land \ldots \land Q \land \ldots \land Q \land \ldots \land R \;\;\defi\;\; P \land \ldots \land Q \land \ldots \land R </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_AND_NOT}}||<math> P \land \ldots \land Q \land \ldots \land \lnot\, Q \land \ldots \land R \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_OR_BTRUE}}||<math> P \lor \ldots \lor \btrue \lor \ldots \lor Q \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_OR_BTRUE}}||<math> P \lor \ldots \lor \btrue \lor \ldots \lor Q \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_OR_BFALSE}}||<math> P \lor \ldots \lor \bfalse \lor \ldots \lor Q \;\;\defi\;\; P \lor \ldots \lor Q </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_OR_BFALSE}}||<math> P \lor \ldots \lor \bfalse \lor \ldots \lor Q \;\;\defi\;\; P \lor \ldots \lor Q </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_OR}}||<math> P \lor \ldots \lor Q \lor \ldots \lor Q \lor \ldots \lor R \;\;\defi\;\; P \lor \ldots \lor Q \lor \ldots \lor R </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_OR_NOT}}||<math> P \lor \ldots \lor Q \lor \ldots \lor \lnot\, Q \land \ldots \land R \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IMP_BTRUE_R}}||<math> P \limp \btrue \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IMP_BTRUE_R}}||<math> P \limp \btrue \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IMP_BTRUE_L}}||<math> \btrue \limp P \;\;\defi\;\; P </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IMP_BTRUE_L}}||<math> \btrue \limp P \;\;\defi\;\; P </math>|| || A | ||
| Line 13: | Line 13: | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IMP_BFALSE_L}}||<math> \bfalse \limp P \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IMP_BFALSE_L}}||<math> \bfalse \limp P \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_IMP}}||<math> P \limp P \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_IMP}}||<math> P \limp P \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_IMP_OR}}||<math> P \land \ldots \land Q \land \ldots \land R \limp Q \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_IMP_AND_NOT_R}}||<math> P \land \ldots \land Q \land \ldots \land R \limp \lnot\, Q \;\;\defi\;\; \lnot\,(P \land \ldots \land Q \land \ldots \land R) </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_IMP_AND_NOT_L}}||<math> P \land \ldots \land \lnot\, Q \land \ldots \land R \limp Q \;\;\defi\;\; \lnot\,(P \land \ldots \land \lnot\, Q \land \ldots \land R) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_EQV}}||<math> P \leqv P \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_EQV}}||<math> P \leqv P \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_EQV_NOT}}||<math> P \leqv \lnot\, P \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_EQV_NOT_NOT}}||<math> \lnot\, P \leqv \lnot\, P \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_BTRUE}}||<math> \lnot\, \btrue \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_BTRUE}}||<math> \lnot\, \btrue \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_BFALSE}}||<math> \lnot\, \bfalse \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_BFALSE}}||<math> \lnot\, \bfalse \;\;\defi\;\; \btrue </math>|| || A | ||
| Line 34: | Line 34: | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_EQUAL_TRUE_R}}||<math> \lnot\, (E = \True ) \;\;\defi\;\; (E = \False ) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_EQUAL_TRUE_R}}||<math> \lnot\, (E = \True ) \;\;\defi\;\; (E = \False ) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_EQUAL_TRUE_L}}||<math> \lnot\, (\True = E) \;\;\defi\;\; (\False = E) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_NOT_EQUAL_TRUE_L}}||<math> \lnot\, (\True = E) \;\;\defi\;\; (\False = E) </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FORALL_AND}}||<math> \forall x \qdot P \land Q \;\;\defi\;\; (\forall x \qdot P) \land (\forall x \qdot Q) </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_EXISTS_OR}}||<math> \exists x \qdot P \lor Q \;\;\defi\;\; (\exists x \qdot P) \lor (\exists x \qdot Q) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FORALL}}||<math> \forall \ldots ,z,\ldots \qdot P(z) \;\;\defi\;\; \forall z \qdot P(z) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FORALL}}||<math> \forall \ldots ,z,\ldots \qdot P(z) \;\;\defi\;\; \forall z \qdot P(z) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_EXISTS}}||<math> \exists \ldots ,z,\ldots \qdot P(z) \;\;\defi\;\; \exists z \qdot P(z) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_EXISTS}}||<math> \exists \ldots ,z,\ldots \qdot P(z) \;\;\defi\;\; \exists z \qdot P(z) </math>|| || A | ||
| Line 43: | Line 43: | ||
{{RRRow}}|*||{{Rulename|SIMP_EQUAL_SING}}||<math> \{ E\} = \{ F\} \;\;\defi\;\; E = F </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_EQUAL_SING}}||<math> \{ E\} = \{ F\} \;\;\defi\;\; E = F </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_TRUE}}||<math> \True = \False \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_TRUE}}||<math> \True = \False \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_SUBSETEQ}}||<math> S \subseteq \mathit{Ty} \;\;\defi\;\; \btrue </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_SUBSETEQ_SING}}||<math> \{ E\} \subseteq S \;\;\defi\;\; E \in S </math>|| where <math>E</math> is a single expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_SUBSETEQ}}||<math> \emptyset \subseteq S \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_SUBSETEQ}}||<math> \emptyset \subseteq S \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_SUBSETEQ}}||<math> S \subseteq S \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_SUBSETEQ}}||<math> S \subseteq S \;\;\defi\;\; \btrue </math>|| || A | ||
| Line 51: | Line 51: | ||
{{RRRow}}|*||{{Rulename|DERIV_SUBSETEQ_BUNION}}||<math> A \bunion \ldots \bunion B \subseteq S \;\;\defi\;\; A \subseteq S \land \ldots \land B \subseteq S </math>|| || M | {{RRRow}}|*||{{Rulename|DERIV_SUBSETEQ_BUNION}}||<math> A \bunion \ldots \bunion B \subseteq S \;\;\defi\;\; A \subseteq S \land \ldots \land B \subseteq S </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DERIV_SUBSETEQ_BINTER}}||<math> S \subseteq A \binter \ldots \binter B \;\;\defi\;\; S \subseteq A \land \ldots \land S \subseteq B </math>|| || M | {{RRRow}}|*||{{Rulename|DERIV_SUBSETEQ_BINTER}}||<math> S \subseteq A \binter \ldots \binter B \;\;\defi\;\; S \subseteq A \land \ldots \land S \subseteq B </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_SUBSET_BUNION}}||<math> A \bunion \ldots \bunion B \subset S \;\;\defi\;\; A \subset S \land \ldots \land B \subset S </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_SUBSET_BINTER}}||<math> S \subset A \binter \ldots \binter B \;\;\defi\;\; S \subset A \land \ldots \land S \subset B </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IN}}||<math> E \in \emptyset \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_IN}}||<math> E \in \emptyset \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_IN}}||<math> B \in \{ A, \ldots , B, \ldots , C\} \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_IN}}||<math> B \in \{ A, \ldots , B, \ldots , C\} \;\;\defi\;\; \btrue </math>|| || A | ||
| Line 60: | Line 60: | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_BINTER}}||<math> S \binter \ldots \binter \mathit{Ty} \binter \ldots \binter T \;\;\defi\;\; S \binter \ldots \binter T </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_BINTER}}||<math> S \binter \ldots \binter \mathit{Ty} \binter \ldots \binter T \;\;\defi\;\; S \binter \ldots \binter T </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_BINTER}}||<math> S \binter \ldots \binter T \binter \ldots \binter T \binter \ldots \binter U \;\;\defi\;\; S \binter \ldots \binter T \binter \ldots \binter U </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_BINTER}}||<math> S \binter \ldots \binter T \binter \ldots \binter T \binter \ldots \binter U \;\;\defi\;\; S \binter \ldots \binter T \binter \ldots \binter U </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_EQUAL_BINTER}}||<math> S \binter \ldots \binter T \binter \ldots \binter U = T \;\;\defi\;\; T \subseteq S \binter \ldots \binter U </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_BUNION}}||<math> S \bunion \ldots \bunion \emptyset \bunion \ldots \bunion T \;\;\defi\;\; S \bunion \ldots \bunion T </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_BUNION}}||<math> S \bunion \ldots \bunion \emptyset \bunion \ldots \bunion T \;\;\defi\;\; S \bunion \ldots \bunion T </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_BUNION}}||<math> S \bunion \ldots \bunion \mathit{Ty} \bunion \ldots \bunion T \;\;\defi\;\; \mathit{Ty} </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_BUNION}}||<math> S \bunion \ldots \bunion \mathit{Ty} \bunion \ldots \bunion T \;\;\defi\;\; \mathit{Ty} </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_BUNION}}||<math> S \bunion \ldots \bunion T \bunion \ldots \bunion T \bunion \ldots \bunion U \;\;\defi\;\; S \bunion \ldots \bunion T \bunion \ldots \bunion U </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_BUNION}}||<math> S \bunion \ldots \bunion T \bunion \ldots \bunion T \bunion \ldots \bunion U \;\;\defi\;\; S \bunion \ldots \bunion T \bunion \ldots \bunion U </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_EQUAL_BUNION}}||<math> S \bunion \ldots \bunion T \bunion \ldots \bunion U = T \;\;\defi\;\; S \bunion \ldots \bunion U \subseteq T </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_SETMINUS}}||<math> S \setminus S \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_MULTI_SETMINUS}}||<math> S \setminus S \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_SETMINUS_R}}||<math> S \setminus \emptyset \;\;\defi\;\; S </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_SETMINUS_R}}||<math> S \setminus \emptyset \;\;\defi\;\; S </math>|| || A | ||
| Line 70: | Line 70: | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_SETMINUS}}||<math> S \setminus \mathit{Ty} \;\;\defi\;\; \emptyset </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_SETMINUS}}||<math> S \setminus \mathit{Ty} \;\;\defi\;\; \emptyset </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_SETMINUS_SETMINUS}}||<math> \mathit{Ty} \setminus (\mathit{Ty} \setminus S) \;\;\defi\;\; S </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_SETMINUS_SETMINUS}}||<math> \mathit{Ty} \setminus (\mathit{Ty} \setminus S) \;\;\defi\;\; S </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_KUNION}}||<math> \union (\mathit{Ty}) \;\;\defi\;\; \mathit{Ta} </math>|| where <math>\mathit{Ty}</math> is a type expression and <math>\mathit{Ty} = \pow (\mathit{Ta})</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_KUNION_POW}}||<math> \union (\pow (S)) \;\;\defi\;\; S </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_KUNION_POW1}}||<math> \union (\pown (S)) \;\;\defi\;\; S </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_KUNION}}||<math> \union \{ \emptyset \} ) \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_KUNION}}||<math> \union \{ \emptyset \} ) \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_QUNION}}||<math> \Union x\qdot \bfalse \mid E \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_QUNION}}||<math> \Union x\qdot \bfalse \mid E \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_KINTER}}||<math> \inter (\{ \emptyset \} ) \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_KINTER}}||<math> \inter (\{ \emptyset \} ) \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_KINTER}}||<math> \inter (\mathit{Ty}) \;\;\defi\;\; \emptyset </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_POW}}||<math> \pow (\emptyset ) \;\;\defi\;\; \{ \emptyset \} </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_POW}}||<math> \pow (\emptyset ) \;\;\defi\;\; \{ \emptyset \} </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_POW1}}||<math> \pown (\emptyset ) \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_POW1}}||<math> \pown (\emptyset ) \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_CPROD_R}}||<math> S \cprod \emptyset \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_CPROD_R}}||<math> S \cprod \emptyset \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_CPROD_L}}||<math> \emptyset \cprod S \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_CPROD_L}}||<math> \emptyset \cprod S \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_COMPSET_EQUAL}}||<math> \{ x \qdot x = E \mid x \} \;\;\defi\;\; \{ E\} </math>|| where <math>x</math> non free in <math>E</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_COMPSET_IN}}||<math> \{ x \qdot x \in S \mid x \} \;\;\defi\;\; S </math>|| where <math>x</math> non free in <math>S</math> || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_COMPSET_BFALSE}}||<math> \{ x \qdot \bfalse \mid x \} \;\;\defi\;\; \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_COMPSET_BFALSE}}||<math> \{ x \qdot \bfalse \mid x \} \;\;\defi\;\; \emptyset </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_COMPSET_BTRUE}}||<math> \{ x \qdot \btrue \mid x \} \;\;\defi\;\; \mathit{Ty} </math>|| where the type od <math>x</math> is <math>\mathit{Ty}</math> || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_COMPSET_BTRUE}}||<math> \{ x \qdot \btrue \mid x \} \;\;\defi\;\; \mathit{Ty} </math>|| where the type od <math>x</math> is <math>\mathit{Ty}</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_SUBSETEQ_COMPSET_L}}||<math> \{ x \qdot P(x) \mid E \} \subseteq S \;\;\defi\;\; \forall x\qdot P(x) \limp E \in S </math>|| where <math>x</math> non free in <math>S</math> || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_EQUAL_COMPSET}}||<math> \{ x \qdot P(x) \mid E \} = \emptyset \;\;\defi\;\; \forall x\qdot \lnot\, P(x) </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_EQUAL_COMPSET}}||<math> \{ x \qdot P(x) \mid E \} = \emptyset \;\;\defi\;\; \forall x\qdot \lnot\, P(x) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_IN_COMPSET}}||<math> F \in \{ x,y,\ldots \qdot P(x,y,\ldots) \mid E(x,y,\ldots) \} \;\;\defi\;\; \exists x,y,\ldots \qdot P(x,y,\ldots) \land E(x,y,\ldots) = F </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_IN_COMPSET}}||<math> F \in \{ x,y,\ldots \qdot P(x,y,\ldots) \mid E(x,y,\ldots) \} \;\;\defi\;\; \exists x,y,\ldots \qdot P(x,y,\ldots) \land E(x,y,\ldots) = F </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_IN_COMPSET_ONEPOINT}}||<math> E \in \{ x \qdot P(x) \mid x \} \;\;\defi\;\; P(E) </math>|| Equivalent to general simplification followed by One Point Rule application with the last conjunct predicate || A | {{RRRow}}|*||{{Rulename|SIMP_IN_COMPSET_ONEPOINT}}||<math> E \in \{ x \qdot P(x) \mid x \} \;\;\defi\;\; P(E) </math>|| Equivalent to general simplification followed by One Point Rule application with the last conjunct predicate || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_SUBSETEQ_COMPSET_R}}||<math> S \subseteq \{ x \qdot P(x) \mid x \} \;\;\defi\;\; \forall y\qdot y \in S \limp P(y) </math>|| where <math>y</math> non free in <math>x, S, \{ x \qdot P(x) \mid x \}</math> || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_OVERL}}||<math> r \ovl \ldots \ovl \emptyset \ovl \ldots \ovl s \;\;\defi\;\; r \ovl \ldots \ovl s </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_OVERL}}||<math> r \ovl \ldots \ovl \emptyset \ovl \ldots \ovl s \;\;\defi\;\; r \ovl \ldots \ovl s </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_OVERL}}||<math>\begin{array}{cl} & r \ovl \ldots \ovl s \ovl \ldots \ovl s \ovl \ldots \ovl u \\ \defi & r \ovl \ldots \ovl \ldots \ovl s \ovl \ldots \ovl u \end{array}</math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_OVERL_CPROD}}||<math> r \ovl (\mathit{Ty} \cprod S) \;\;\defi\;\; (\mathit{Ty} \cprod S) </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_KBOOL_BTRUE}}||<math> \bool (\btrue ) \;\;\defi\;\; \True </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_KBOOL_BTRUE}}||<math> \bool (\btrue ) \;\;\defi\;\; \True </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_KBOOL_BFALSE}}||<math> \bool (\bfalse ) \;\;\defi\;\; \False </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_KBOOL_BFALSE}}||<math> \bool (\bfalse ) \;\;\defi\;\; \False </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_SUBSETEQ_BUNION_SING}}||<math> S \bunion \{ F\} \subseteq T \;\;\defi\;\; S \subseteq T \land F \in T </math>|| where <math>F</math> is a single expression || M | ||
{{RRRow}}| ||{{Rulename|DEF_FINITE}}||<math> \finite(S) \;\;\defi\;\; \exists n,f\qdot n\in\nat\land f\in 1\upto n \tbij S </math>|| || M | {{RRRow}}| ||{{Rulename|DEF_FINITE}}||<math> \finite(S) \;\;\defi\;\; \exists n,f\qdot n\in\nat\land f\in 1\upto n \tbij S </math>|| || M | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_FINITE}}||<math> \finite (\emptyset ) \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_FINITE}}||<math> \finite (\emptyset ) \;\;\defi\;\; \btrue </math>|| || A | ||
| Line 104: | Line 104: | ||
{{RRRow}}|*||{{Rulename|SIMP_FINITE_CONVERSE}}||<math> \finite (r^{-1} ) \;\;\defi\;\; \finite (r) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FINITE_CONVERSE}}||<math> \finite (r^{-1} ) \;\;\defi\;\; \finite (r) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_FINITE_UPTO}}||<math> \finite (a \upto b) \;\;\defi\;\; \btrue </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_FINITE_UPTO}}||<math> \finite (a \upto b) \;\;\defi\;\; \btrue </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_BINTER_L}}||<math> \finite (S \binter T) \;\;\defi\;\; \finite (S) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_BINTER_R}}||<math> \finite (S \binter T) \;\;\defi\;\; \finite (T) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_SETMINUS}}||<math> \finite (S \setminus T) \;\;\defi\;\; \finite (S) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_DOMRES}}||<math> \finite (S \domres r) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_RANRES}}||<math> \finite (r \ranres S) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_DOMSUB}}||<math> \finite (S \domsub r) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_RANSUB}}||<math> \finite (r \ransub S) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_RELIMAGE}}||<math> \finite (r[S]) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_CPROD}}||<math> \finite (S \cprod T) \;\;\defi\;\; \finite (S) \land \finite (T) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_OVERL}}||<math> \finite (r \ovl s) \;\;\defi\;\; \finite (r) \land \finite (s) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|SIMP_FINITE_REL}}||<math> \finite (S \rel T) \;\;\defi\;\; \finite (S) \land \finite (T) </math>|| || M | {{RRRow}}|*||{{Rulename|SIMP_FINITE_REL}}||<math> \finite (S \rel T) \;\;\defi\;\; \finite (S) \land \finite (T) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_FCOMP}}||<math> \finite (r \fcomp s) \;\;\defi\;\; \finite (r) \land \finite (s) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_BCOMP}}||<math> \finite (r \bcomp s) \;\;\defi\;\; \finite (r) \land \finite (s) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_DPROD}}||<math> \finite (r \dprod s) \;\;\defi\;\; \finite (r) \land \finite (s) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_PPROD}}||<math> \finite (r \pprod s) \;\;\defi\;\; \finite (r) \land \finite (s) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_COMPSET}}||<math> \finite (\{ x \qdot x \in S \land \ldots \land P \mid x\} ) \;\;\defi\;\; \finite (S) </math>|| where <math>x</math> non free in <math>S</math> || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_RAN}}||<math> \finite (\ran (r)) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_DOM}}||<math> \finite (\dom (r)) \;\;\defi\;\; \finite (r) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_QUNION}}||<math> \finite (\Union x \qdot P \mid E) \;\;\defi\;\; \forall x \qdot P \limp \finite (E) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_QINTER}}||<math> \finite (\Inter x \qdot P \mid E) \;\;\defi\;\; \exists x \qdot P \land \finite (E) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_ID}}||<math> \finite (\id) \;\;\defi\;\; \finite (S) </math>|| where <math>\id</math> has type <math>\pow(S \cprod S)</math> || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_NATURAL}}||<math> \finite (\nat ) \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_NATURAL1}}||<math> \finite (\natn ) \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_INTEGER}}||<math> \finite (\intg ) \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_FINITE_LAMBDA}}||<math> \finite (\lambda x \qdot P \mid E) \;\;\defi\;\; \finite (\{ x \qdot P \mid x\} ) </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_EQUAL_EMPTY}}||<math> \mathit{Ty} = \emptyset \;\;\defi\;\; \bfalse </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_EQUAL_EMPTY}}||<math> \mathit{Ty} = \emptyset \;\;\defi\;\; \bfalse </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_IN}}||<math> t \in \mathit{Ty} \;\;\defi\;\; \btrue </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_IN}}||<math> t \in \mathit{Ty} \;\;\defi\;\; \btrue </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
| Line 140: | Line 140: | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_SUBSET_R}}||<math> S \subset \emptyset \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_SUBSET_R}}||<math> S \subset \emptyset \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}| ||{{Rulename|SIMP_SPECIAL_SUBSET_L}}||<math> \emptyset \subset S \;\;\defi\;\; S \neq \emptyset </math>|| || A | {{RRRow}}| ||{{Rulename|SIMP_SPECIAL_SUBSET_L}}||<math> \emptyset \subset S \;\;\defi\;\; S \neq \emptyset </math>|| || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_TYPE_SUBSET_L}}||<math> S \subset \mathit{Ty} \;\;\defi\;\; S \neq \mathit{Ty} </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|SIMP_MULTI_SUBSET}}||<math> S \subset S \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|*||{{Rulename|DISTRI_AND_OR}}||<math> P \land (Q \lor R) \;\;\defi\;\; (P \land Q) \lor (P \land R) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_AND_OR}}||<math> P \land (Q \lor R) \;\;\defi\;\; (P \land Q) \lor (P \land R) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_OR_AND}}||<math> P \lor (Q \land R) \;\;\defi\;\; (P \lor Q) \land (P \lor R) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_OR_AND}}||<math> P \lor (Q \land R) \;\;\defi\;\; (P \lor Q) \land (P \lor R) </math>|| || M | ||
| Line 171: | Line 171: | ||
{{RRRow}}|*||{{Rulename|DISTRI_BUNION_BINTER}}||<math> S \bunion (T \binter U) \;\;\defi\;\; (S \bunion T) \binter (S \bunion U) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_BUNION_BINTER}}||<math> S \bunion (T \binter U) \;\;\defi\;\; (S \bunion T) \binter (S \bunion U) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DISTRI_BINTER_BUNION}}||<math> S \binter (T \bunion U) \;\;\defi\;\; (S \binter T) \bunion (S \binter U) </math>|| || M | {{RRRow}}|*||{{Rulename|DISTRI_BINTER_BUNION}}||<math> S \binter (T \bunion U) \;\;\defi\;\; (S \binter T) \bunion (S \binter U) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_BINTER_SETMINUS}}||<math> S \binter (T \setminus U) \;\;\defi\;\; (S \binter T) \setminus (S \binter U) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_SETMINUS_BUNION}}||<math> S \setminus (T \bunion U) \;\;\defi\;\; S \setminus T \setminus U </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DERIV_TYPE_SETMINUS_BINTER}}||<math> \mathit{Ty} \setminus (S \binter T) \;\;\defi\;\; (\mathit{Ty} \setminus S) \bunion (\mathit{Ty} \setminus T) </math>|| where <math>\mathit{Ty}</math> is a type expression || M | {{RRRow}}|*||{{Rulename|DERIV_TYPE_SETMINUS_BINTER}}||<math> \mathit{Ty} \setminus (S \binter T) \;\;\defi\;\; (\mathit{Ty} \setminus S) \bunion (\mathit{Ty} \setminus T) </math>|| where <math>\mathit{Ty}</math> is a type expression || M | ||
{{RRRow}}|*||{{Rulename|DERIV_TYPE_SETMINUS_BUNION}}||<math> \mathit{Ty} \setminus (S \bunion T) \;\;\defi\;\; (\mathit{Ty} \setminus S) \binter (\mathit{Ty} \setminus T) </math>|| where <math>\mathit{Ty}</math> is a type expression || M | {{RRRow}}|*||{{Rulename|DERIV_TYPE_SETMINUS_BUNION}}||<math> \mathit{Ty} \setminus (S \bunion T) \;\;\defi\;\; (\mathit{Ty} \setminus S) \binter (\mathit{Ty} \setminus T) </math>|| where <math>\mathit{Ty}</math> is a type expression || M | ||
{{RRRow}}|*||{{Rulename|DERIV_TYPE_SETMINUS_SETMINUS}}||<math> \mathit{Ty} \setminus (S \setminus T) \;\;\defi\;\; (\mathit{Ty} \setminus S) \bunion T </math>|| where <math>\mathit{Ty}</math> is a type expression || M | {{RRRow}}|*||{{Rulename|DERIV_TYPE_SETMINUS_SETMINUS}}||<math> \mathit{Ty} \setminus (S \setminus T) \;\;\defi\;\; (\mathit{Ty} \setminus S) \bunion T </math>|| where <math>\mathit{Ty}</math> is a type expression || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CPROD_BINTER}}||<math> S \cprod (T \binter U) \;\;\defi\;\; (S \cprod T) \binter (S \cprod U) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CPROD_BUNION}}||<math> S \cprod (T \bunion U) \;\;\defi\;\; (S \cprod T) \bunion (S \cprod U) </math>|| || M | ||
{{RRRow}}| | {{RRRow}}|||{{Rulename|DISTRI_CPROD_SETMINUS}}||<math> S \cprod (T \setminus U) \;\;\defi\;\; (S \cprod T) \setminus (S \cprod U) </math>|| || M | ||
{{RRRow}}|*||{{Rulename|DERIV_SUBSETEQ}}||<math> S \subseteq T \;\;\defi\;\; (\mathit{Ty} \setminus T) \subseteq (\mathit{Ty} \setminus S) </math>|| where <math>\pow (\mathit{Ty})</math> is the type of <math>S</math> and <math>T</math> || M | {{RRRow}}|*||{{Rulename|DERIV_SUBSETEQ}}||<math> S \subseteq T \;\;\defi\;\; (\mathit{Ty} \setminus T) \subseteq (\mathit{Ty} \setminus S) </math>|| where <math>\pow (\mathit{Ty})</math> is the type of <math>S</math> and <math>T</math> || M | ||
{{RRRow}}|*||{{Rulename|DERIV_EQUAL}}||<math> S = T \;\;\defi\;\; S \subseteq T \land T \subseteq S </math>|| where <math>\pow (\mathit{Ty})</math> is the type of <math>S</math> and <math>T</math> || M | {{RRRow}}|*||{{Rulename|DERIV_EQUAL}}||<math> S = T \;\;\defi\;\; S \subseteq T \land T \subseteq S </math>|| where <math>\pow (\mathit{Ty})</math> is the type of <math>S</math> and <math>T</math> || M | ||
Revision as of 10:17, 21 December 2009
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_AND_BTRUE |
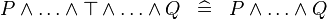 |
A | |
| * | SIMP_SPECIAL_AND_BFALSE |
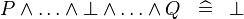 |
A | |
SIMP_MULTI_AND |
 |
A | ||
SIMP_MULTI_AND_NOT |
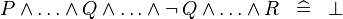 |
A | ||
| * | SIMP_SPECIAL_OR_BTRUE |
 |
A | |
| * | SIMP_SPECIAL_OR_BFALSE |
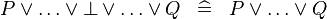 |
A | |
SIMP_MULTI_OR |
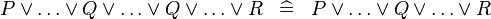 |
A | ||
SIMP_MULTI_OR_NOT |
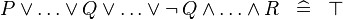 |
A | ||
| * | SIMP_SPECIAL_IMP_BTRUE_R |
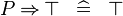 |
A | |
| * | SIMP_SPECIAL_IMP_BTRUE_L |
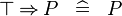 |
A | |
| * | SIMP_SPECIAL_IMP_BFALSE_R |
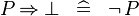 |
A | |
| * | SIMP_SPECIAL_IMP_BFALSE_L |
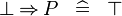 |
A | |
| * | SIMP_MULTI_IMP |
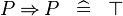 |
A | |
SIMP_MULTI_IMP_OR |
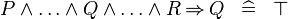 |
A | ||
SIMP_MULTI_IMP_AND_NOT_R |
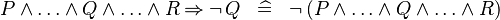 |
A | ||
SIMP_MULTI_IMP_AND_NOT_L |
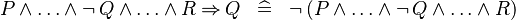 |
A | ||
| * | SIMP_MULTI_EQV |
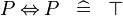 |
A | |
SIMP_MULTI_EQV_NOT |
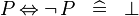 |
A | ||
SIMP_MULTI_EQV_NOT_NOT |
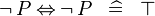 |
A | ||
| * | SIMP_SPECIAL_NOT_BTRUE |
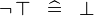 |
A | |
| * | SIMP_SPECIAL_NOT_BFALSE |
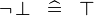 |
A | |
| * | SIMP_NOT_NOT |
 |
A | |
| * | SIMP_NOTEQUAL |
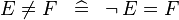 |
A | |
| * | SIMP_NOTIN |
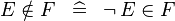 |
A | |
| * | SIMP_NOTSUBSET |
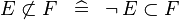 |
A | |
| * | SIMP_NOTSUBSETEQ |
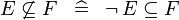 |
A | |
| * | SIMP_NOT_LE |
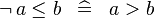 |
A | |
| * | SIMP_NOT_GE |
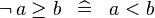 |
A | |
| * | SIMP_NOT_LT |
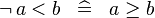 |
A | |
| * | SIMP_NOT_GT |
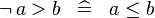 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_FALSE_R |
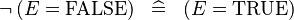 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_FALSE_L |
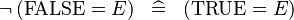 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_TRUE_R |
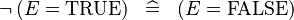 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_TRUE_L |
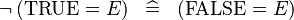 |
A | |
SIMP_FORALL_AND |
 |
A | ||
SIMP_EXISTS_OR |
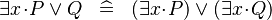 |
A | ||
| * | SIMP_FORALL |
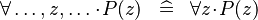 |
A | |
| * | SIMP_EXISTS |
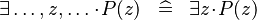 |
A | |
| * | SIMP_MULTI_EQUAL |
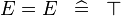 |
A | |
| * | SIMP_MULTI_NOTEQUAL |
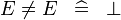 |
A | |
| * | SIMP_EQUAL_MAPSTO |
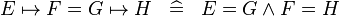 |
A | |
| * | SIMP_EQUAL_SING |
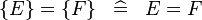 |
A | |
| * | SIMP_SPECIAL_EQUAL_TRUE |
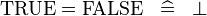 |
A | |
SIMP_TYPE_SUBSETEQ |
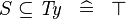 |
where  is a type expression is a type expression |
A | |
SIMP_SUBSETEQ_SING |
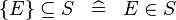 |
where  is a single expression is a single expression |
A | |
| * | SIMP_SPECIAL_SUBSETEQ |
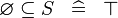 |
A | |
| * | SIMP_MULTI_SUBSETEQ |
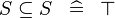 |
A | |
| * | SIMP_SUBSETEQ_BUNION |
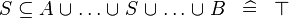 |
A | |
| * | SIMP_SUBSETEQ_BINTER |
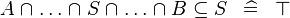 |
A | |
| * | DERIV_SUBSETEQ_BUNION |
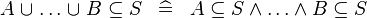 |
M | |
| * | DERIV_SUBSETEQ_BINTER |
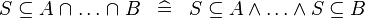 |
M | |
SIMP_SUBSET_BUNION |
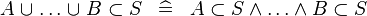 |
A | ||
SIMP_SUBSET_BINTER |
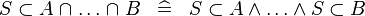 |
A | ||
| * | SIMP_SPECIAL_IN |
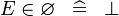 |
A | |
| * | SIMP_MULTI_IN |
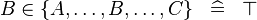 |
A | |
| * | SIMP_IN_SING |
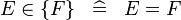 |
A | |
| * | SIMP_MULTI_SETENUM |
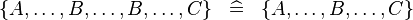 |
A | |
| * | SIMP_SPECIAL_BINTER |
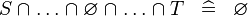 |
A | |
| * | SIMP_TYPE_BINTER |
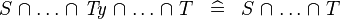 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_BINTER |
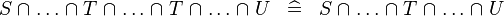 |
A | |
SIMP_MULTI_EQUAL_BINTER |
 |
A | ||
| * | SIMP_SPECIAL_BUNION |
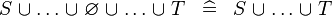 |
A | |
| * | SIMP_TYPE_BUNION |
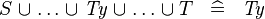 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_BUNION |
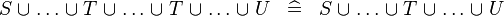 |
A | |
SIMP_MULTI_EQUAL_BUNION |
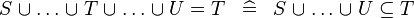 |
A | ||
| * | SIMP_MULTI_SETMINUS |
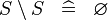 |
A | |
| * | SIMP_SPECIAL_SETMINUS_R |
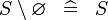 |
A | |
| * | SIMP_SPECIAL_SETMINUS_L |
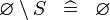 |
A | |
| * | SIMP_TYPE_SETMINUS |
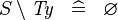 |
where  is a type expression is a type expression |
A |
| * | SIMP_TYPE_SETMINUS_SETMINUS |
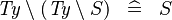 |
where  is a type expression is a type expression |
A |
SIMP_TYPE_KUNION |
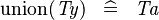 |
where  is a type expression and is a type expression and 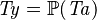 |
A | |
SIMP_KUNION_POW |
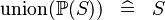 |
A | ||
SIMP_KUNION_POW1 |
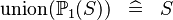 |
A | ||
SIMP_SPECIAL_KUNION |
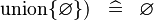 |
A | ||
SIMP_SPECIAL_QUNION |
 |
A | ||
SIMP_SPECIAL_KINTER |
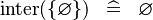 |
A | ||
SIMP_TYPE_KINTER |
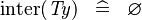 |
where  is a type expression is a type expression |
A | |
SIMP_SPECIAL_POW |
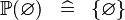 |
A | ||
SIMP_SPECIAL_POW1 |
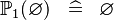 |
A | ||
SIMP_SPECIAL_CPROD_R |
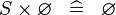 |
A | ||
SIMP_SPECIAL_CPROD_L |
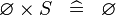 |
A | ||
SIMP_COMPSET_EQUAL |
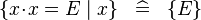 |
where  non free in non free in  |
A | |
SIMP_COMPSET_IN |
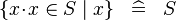 |
where  non free in non free in  |
A | |
SIMP_SPECIAL_COMPSET_BFALSE |
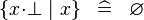 |
A | ||
SIMP_SPECIAL_COMPSET_BTRUE |
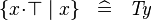 |
where the type od  is is  |
A | |
SIMP_SUBSETEQ_COMPSET_L |
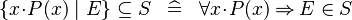 |
where  non free in non free in  |
A | |
SIMP_SPECIAL_EQUAL_COMPSET |
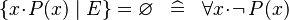 |
A | ||
| * | SIMP_IN_COMPSET |
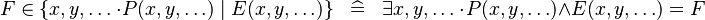 |
A | |
| * | SIMP_IN_COMPSET_ONEPOINT |
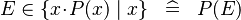 |
Equivalent to general simplification followed by One Point Rule application with the last conjunct predicate | A |
SIMP_SUBSETEQ_COMPSET_R |
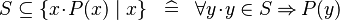 |
where 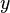 non free in non free in 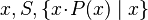 |
A | |
SIMP_SPECIAL_OVERL |
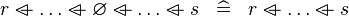 |
A | ||
SIMP_MULTI_OVERL |
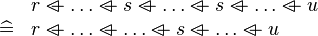 |
A | ||
SIMP_TYPE_OVERL_CPROD |
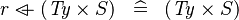 |
where  is a type expression is a type expression |
A | |
| * | SIMP_SPECIAL_KBOOL_BTRUE |
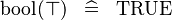 |
A | |
| * | SIMP_SPECIAL_KBOOL_BFALSE |
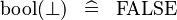 |
A | |
DISTRI_SUBSETEQ_BUNION_SING |
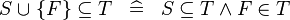 |
where 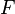 is a single expression is a single expression |
M | |
DEF_FINITE |
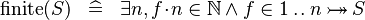 |
M | ||
| * | SIMP_SPECIAL_FINITE |
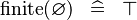 |
A | |
| * | SIMP_FINITE_SETENUM |
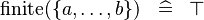 |
A | |
| * | SIMP_FINITE_BUNION |
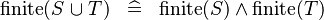 |
A | |
| * | SIMP_FINITE_POW |
 |
A | |
| * | DERIV_FINITE_CPROD |
 |
A | |
| * | SIMP_FINITE_CONVERSE |
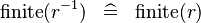 |
A | |
| * | SIMP_FINITE_UPTO |
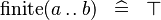 |
A | |
SIMP_FINITE_BINTER_L |
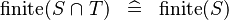 |
M | ||
SIMP_FINITE_BINTER_R |
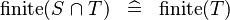 |
M | ||
SIMP_FINITE_SETMINUS |
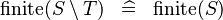 |
M | ||
SIMP_FINITE_DOMRES |
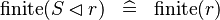 |
M | ||
SIMP_FINITE_RANRES |
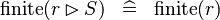 |
M | ||
SIMP_FINITE_DOMSUB |
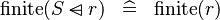 |
M | ||
SIMP_FINITE_RANSUB |
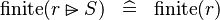 |
M | ||
SIMP_FINITE_RELIMAGE |
![\finite (r[S]) \;\;\defi\;\; \finite (r)](/images/math/5/c/e/5ce3a57b43258dc4a25597542670990a.png) |
M | ||
SIMP_FINITE_CPROD |
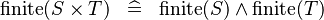 |
M | ||
SIMP_FINITE_OVERL |
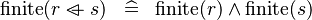 |
M | ||
| * | SIMP_FINITE_REL |
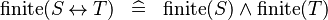 |
M | |
SIMP_FINITE_FCOMP |
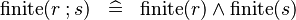 |
M | ||
SIMP_FINITE_BCOMP |
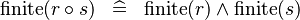 |
M | ||
SIMP_FINITE_DPROD |
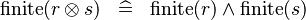 |
M | ||
SIMP_FINITE_PPROD |
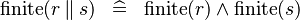 |
M | ||
SIMP_FINITE_COMPSET |
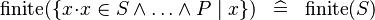 |
where  non free in non free in  |
M | |
SIMP_FINITE_RAN |
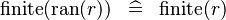 |
M | ||
SIMP_FINITE_DOM |
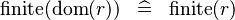 |
M | ||
SIMP_FINITE_QUNION |
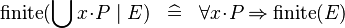 |
M | ||
SIMP_FINITE_QINTER |
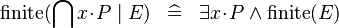 |
M | ||
SIMP_FINITE_ID |
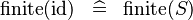 |
where 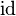 has type has type 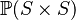 |
A | |
SIMP_FINITE_NATURAL |
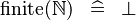 |
A | ||
SIMP_FINITE_NATURAL1 |
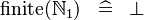 |
A | ||
SIMP_FINITE_INTEGER |
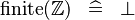 |
A | ||
SIMP_FINITE_LAMBDA |
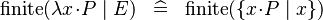 |
A | ||
| * | SIMP_TYPE_EQUAL_EMPTY |
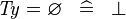 |
where  is a type expression is a type expression |
A |
| * | SIMP_TYPE_IN |
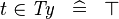 |
where  is a type expression is a type expression |
A |
SIMP_SPECIAL_FORALL_BTRUE |
 |
A | ||
SIMP_SPECIAL_FORALL_BFALSE |
 |
A | ||
SIMP_SPECIAL_EXISTS_BTRUE |
 |
A | ||
SIMP_SPECIAL_EXISTS_BFALSE |
 |
A | ||
| * | SIMP_SPECIAL_EQV_BTRUE |
 |
A | |
| * | SIMP_SPECIAL_EQV_BFALSE |
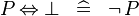 |
A | |
| * | DEF_SUBSET |
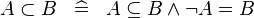 |
A | |
SIMP_SPECIAL_SUBSET_R |
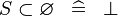 |
A | ||
SIMP_SPECIAL_SUBSET_L |
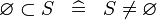 |
A | ||
SIMP_TYPE_SUBSET_L |
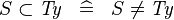 |
where  is a type expression is a type expression |
A | |
SIMP_MULTI_SUBSET |
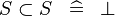 |
A | ||
| * | DISTRI_AND_OR |
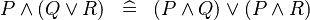 |
M | |
| * | DISTRI_OR_AND |
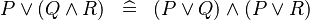 |
M | |
| * | DEF_OR |
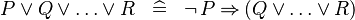 |
M | |
| * | DERIV_IMP |
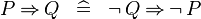 |
M | |
| * | DERIV_IMP_IMP |
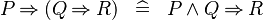 |
M | |
| * | DISTRI_IMP_AND |
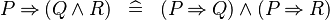 |
M | |
| * | DISTRI_IMP_OR |
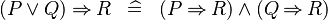 |
M | |
| * | DEF_EQV |
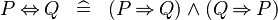 |
M | |
| * | DISTRI_NOT_AND |
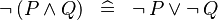 |
M | |
| * | DISTRI_NOT_OR |
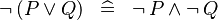 |
M | |
| * | DERIV_NOT_IMP |
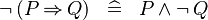 |
M | |
| * | DERIV_NOT_FORALL |
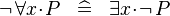 |
M | |
| * | DERIV_NOT_EXISTS |
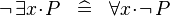 |
M | |
| * | DEF_SPECIAL_NOT_EQUAL |
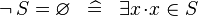 |
M | |
| * | DEF_IN_MAPSTO |
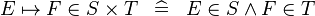 |
M | |
| * | DEF_IN_POW |
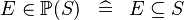 |
M | |
| * | DEF_IN_POW1 |
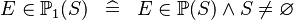 |
M | |
| * | DEF_SUBSETEQ |
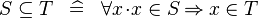 |
M | |
| * | DEF_IN_BUNION |
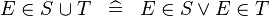 |
M | |
| * | DEF_IN_BINTER |
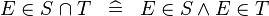 |
M | |
| * | DEF_IN_SETMINUS |
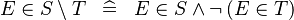 |
M | |
| * | DEF_IN_SETENUM |
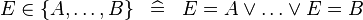 |
M | |
| * | DEF_IN_KUNION |
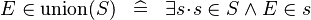 |
M | |
| * | DEF_IN_QUNION |
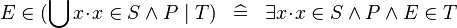 |
M | |
| * | DEF_IN_KINTER |
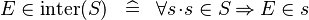 |
M | |
| * | DEF_IN_QINTER |
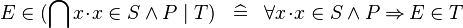 |
M | |
| * | DEF_IN_UPTO |
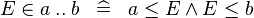 |
M | |
| * | DISTRI_BUNION_BINTER |
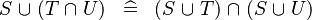 |
M | |
| * | DISTRI_BINTER_BUNION |
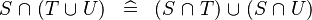 |
M | |
DISTRI_BINTER_SETMINUS |
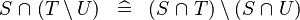 |
M | ||
DISTRI_SETMINUS_BUNION |
 |
M | ||
| * | DERIV_TYPE_SETMINUS_BINTER |
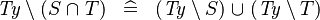 |
where  is a type expression is a type expression |
M |
| * | DERIV_TYPE_SETMINUS_BUNION |
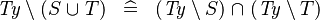 |
where  is a type expression is a type expression |
M |
| * | DERIV_TYPE_SETMINUS_SETMINUS |
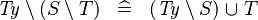 |
where  is a type expression is a type expression |
M |
DISTRI_CPROD_BINTER |
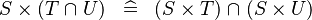 |
M | ||
DISTRI_CPROD_BUNION |
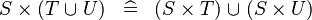 |
M | ||
DISTRI_CPROD_SETMINUS |
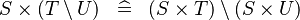 |
M | ||
| * | DERIV_SUBSETEQ |
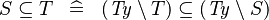 |
where 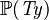 is the type of is the type of  and and  |
M |
| * | DERIV_EQUAL |
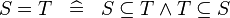 |
where 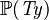 is the type of is the type of  and and  |
M |
| * | DERIV_SUBSETEQ_SETMINUS_L |
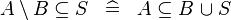 |
M | |
| * | DERIV_SUBSETEQ_SETMINUS_R |
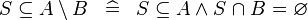 |
M | |
| * | DEF_PARTITION |
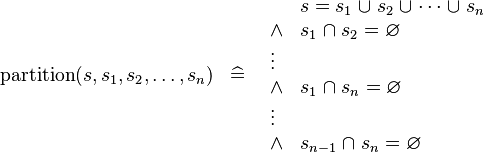 |
AM |