Structured Types

Structured Types as Projections

The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. Nevertheless it is possible to model structured types using projection functions to represent the fields/ attributes. For example, suppose we wish to model a structured type C with fields e and f (with type E and F respectively). Let us use the following syntax for this (not part of Event-B):

$\begin{array}{lcl} C &::& e\in E\\ && f \in F \end{array}$

$\begin{array}{l} \textbf{SETS}~~ C\\ \textbf{CONSTANTS}~~ e,~ f\\ \textbf{AXIOMS}\\ \begin{array}{l} e \in C \tfun E\\ f \in C \tfun F\\ \end{array} \end{array}$

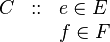
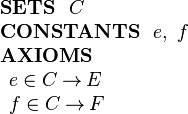
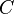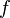We can model this structure in Event-B by introducing (in a context) a set $C$ and two functions $e$ and $f$ as constants as follows:

Names in the proof tree: Predicate Prover

Names in the preferences: PP restricted, PP after lasso, PP unrestricted

Input: In the configuration "restricted" all selected hypotheses and the goal are passed to New PP. In the configuration "after lasso" a lasso operation is applied to the selected hypotheses and the goal and the result is passed to New PP. The lasso operation selects any unselected hypothesis that has a common symbol with the goal or a hypothesis that was selected before. In the configuration "unrestricted" all the available hypotheses are passed to New PP.

How the Prover Proceeds: First, all function and predicate symbols that are different from "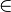$\in$" and not related to arithmetic are translated away. For example 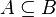$A \subseteq B$ is translated to 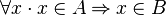$\forall x\cdot x \in A \limp x \in B$. Then New PP translates the proof obligation to CNF (conjunctive normal form) and applies a combination of unit resolution and the Davis Putnam algorithm.

Some Strengths:

• New PP outputs a set of "used hypotheses". If an unused hypotheses changes, the old proof can be reused.
• New PP has limited support for equational reasoning.