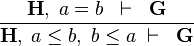Adding Reasoners(How to extend Rodin Tutorial)
Principles
Rodin support several provers. Some are embedded such as NewPP, or the sequent prover which will talk about here, and some are added through plug-ins (as the Atelier B provers : ML, PP, P0, etc).
Contributing to Rodin sequent prover is done by adding tactics. These tactics apply on proof tree nodes which often involve a set of reasoners. The reasoners apply on the sequent of a given proof tree node. A reasoner is (and has to be) quite "rough" : it shall take a given sequent and calculate a proof rule that will apply on it (if possible), whereas a tactic could be smarter. Indeed, a tactic can involve several reasoners, thus apply them in loops, and combine them, or even call other tactics. A tactic can be either automatic (auto tactic and/or post tactic) or manual (using providers in the UI that paint their applications in red on formulas).
A reasoner encapsulates a kind of "proof step", also called "proof rule". The sequent prover provides a set of tactics applying proof rules (and other tactics). These rules are either rewriting rules (see rewriting rules) or inference rules (see inference rules) that helps the user in the interactive proof mode. It is actually a really critical piece of code, that one human should understand at first sight, and be convinced about its correctness. If one codes a wrong reasoner, one breaks the whole soundness of proofs done within Rodin! As they are written in pure java, and accorded to the previous considerations, they have to be the simpliest and most readable as possible. Finally, it is needed to write tests that cover all the possible cases of application of one given reasoner (this will not be detailed here).
In this part
In this part we will see how to contribute to the sequent prover of Rodin by encapsulating a new proof rule within a reasoner and add a tactic to the sequent prover of Rodin that will encapsulate this reasoner. The rule we want to apply is the following: