Rodin Proving Perspective

<prev: The Proof Obligation Explorer

>next: The Mathematical Language

^up: User_Manual_index

Overview

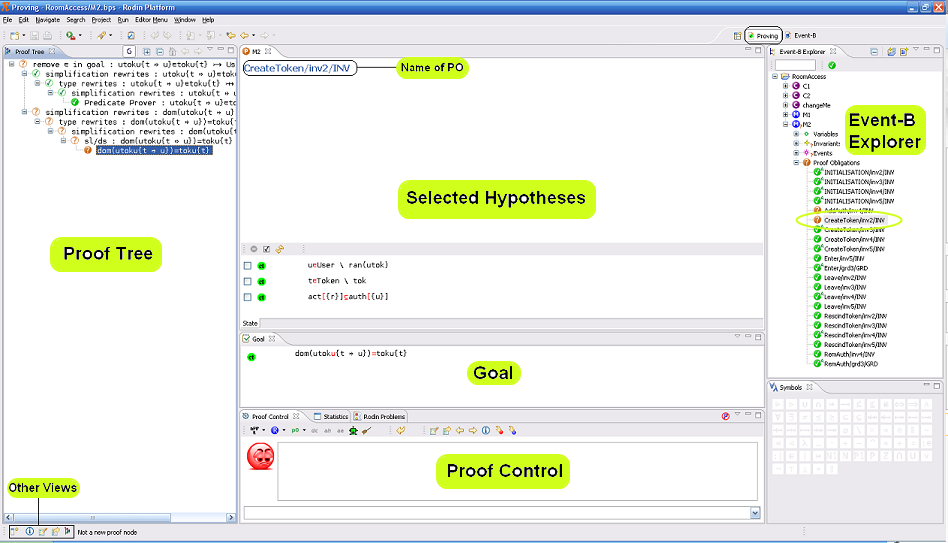
The Proving Perspective is made of a number of windows (views): the Proof Tree, the Goal, the Selected Hypotheses, the Proof Control, the Proof Information, and the Search Hypotheses. In subsequent sections, we study each of these windows. Below is a screenshot of the proving perspective:

Loading a Proof

In order to load a proof, switch to the Proving Perspective, select the project from the Event-B Explorer, select and expand the component (context or machine), finally select the proof obligation of interest. The corresponding proof will be loaded.

The Proof Tree

The proof tree describe each individual proof step in the proof. The proof tree can be seen in its corresponding window as seen in the following screenshot:

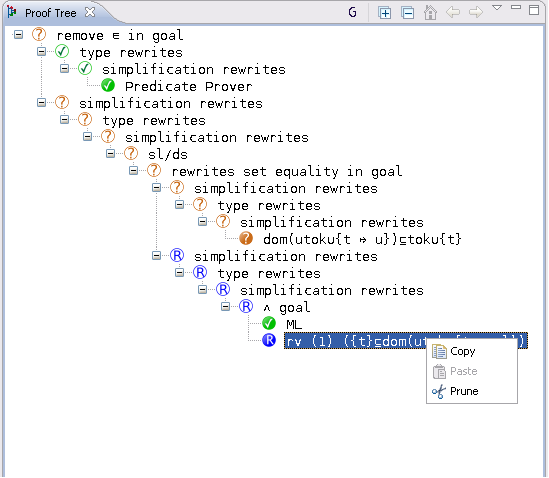
Each line in the tree corresponds to a node which is a sequent. A line is right shifted when the corresponding node is a direct descendant of the node of the previous line. Each node is labelled with a comment (description) explaining how it can be discharged. By selecting a node in the proof tree, the corresponding sequent is loaded: the hypotheses of the sequent are loaded to the Selected Hypotheses window, and the goal of the sequent is loaded to the Goal window.

Decoration

The leaves of the tree are decorated with three kinds of logos:

• a green logo with a "$\surd$" in it means that this leaf is discharged,
• a brown logo with a "?" in it means that this leaf is not discharged,
• a blue logo with a "R" in it means that this leaf has been reviewed.

Internal nodes in the proof tree are decorated in the same (but lighter) way. Note that a "reviewed" leaf is one that is not discharged yet by the prover. Instead, it has been "seen" by the user who decided to have it discharged later. Marking nodes as "reviewed" is very convenient in order to perform an interactive proof in a gradual fashion. In order to discharge a "reviewed" node, select it and prune the tree at that node: the node will become "brown" again (undischarged) and you can now try to discharge it.

Navigation within the Proof Tree

On top of the proof tree window, one can see three buttons:

• the "G" buttons allows you to see the goal of the sequent corresponding to the node
• the "+" button allows you to fully expand the proof tree
• the "-" allows you to fully collapse the tree: only the root stays visible.

Manipulating the Proof Tree

Hiding

The little triangle (with a "+" or "-" inside) next to each node in the proof tree allows you to expand or collapse the subtree starting at that node.

Pruning

The proof tree can be pruned from a node: it means that the subtree starting at that node is eliminated. The node in question becomes a leaf and is brown decorated. This allows you to resume the proof from that node. After selecting a sequent in the proof tree, pruning can be performed by right-clicking and then selecting "Prune".

Note that after pruning, the post-tactic is not applied to the new current sequent: if needed you have to press the "post-tactic" button in the Proof Control window. This happens in particular when you want to redo a proof from the beginning: you prune the proof tree from the root node and then you have to press the "post-tactic" button in order to be in exactly the same situation as the one delivered automatically initially.

When you want to redo a proof from a certain node, it might be advisable to do it after copying the tree so that in case your new proof fails you can still resume the previous situation by pasting the copied version (see next section).

Copy/Paste

By selecting a node in the proof tree and then clicking on the right key of the mouse, you can copy the part of the proof tree starting at that sequent: it can later be pasted in the same way. This allows you to reuse part of a proof tree in the same (or even another) proof.

Goal and Selected Hypotheses

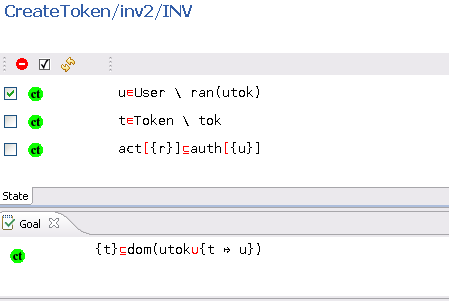
The "Goal" and "Selected Hypotheses" windows display the current sequent you have to prove at a given moment in the proof. Here is an example:

A selected hypothesis can be deselected (and as a result becomes hidden) by first clicking in the box (check box) situated next to it (you can click on several boxes) and then by pressing the red (-) button at the top of the selected hypothesis window:

Here is the result:

Notice that the deselected hypotheses are not lost: you can get them back by means of the Search Hypotheses window. The other two buttons next to the red (-) button allow the user (in the order of their appearance from left to right) to select all hypotheses as well as inverse the current selection.

The (ct) button next to the goal allows you to do a proof by contradiction: by pressing it, the negation of the goal becomes a selected hypothesis whereas the goal becomes "⊥".

The (ct) button next to a selected hypothesis allows you to do another kind of proof by contradiction: by pressing it, the negation of the concerned hypothesis becomes the goal whereas the negated goal becomes an hypothesis.

Applying Proof Rules

The red hyperlinks as well as the (ct) buttons allows the user to carry out interactive proofs. They are used to invoke proof rules (rewrite rules as well as inference rules).

Rewrite Rules

Rewrite rules are one-directional equalities (and equivalences) that can be used to simplify formulas (the goal or a single hypothesis). A rewrite rule is applied from left to right either in the goal or in one of the selected hypotheses, when its side condition holds.

A rewrite rule is applied either automatically (A) or manually (M):

• automatically, when post tactics are enabled. These rules are equivalence simplification laws.
• manually, through an interactive command. These rules gathers non equivalence laws, definition laws, distributivity laws and derived laws.

Each rule is named after the following elements:

• The law category: simplification law (SIMP), definition law (DEF), distributivity law (DISTRI), or else derived law (DERIV).
• Particularity on terminal elements of the left part of the rule (optional): special element (SPECIAL) such as the empty-set, type expression (TYPE), same element occurring more then once (MULTI), literal (LIT). A type expression is either a basic type (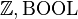$\intg, \Bool$, any carrier set), or 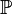$\pow$(type expression), or type expression$\cprod$type expression.
• One or more elements describing from top to down the left part of the rule, eg. predicate AND, expression BUNION.
• Detail to localize those elements (optional): left (L), right (R).

Rewrite rules having an equivalence operator in their left part may also describe other rules. eg: the rule:

$\True = \False \;\;\defi\;\; \bfalse$

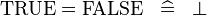
should also produce the rule:

$\False = \True \;\;\defi\;\; \bfalse$

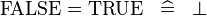
For associative operators in connection with distributive laws as in:

$P \land (Q \lor \ldots \lor R)$

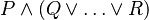
it has been decided to put the "button" on the first associative/commutative operator (here 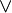$\lor$). Pressing that button will generate a menu: the first option of this menu will be to distribute all associative/commutative operators, the second option will be to distribute only the first associative/commutative operator. In the following presentation, to simplify matters, we write associative/commutative operators with two parameters only, but it must always be understood implicitly that we have a sequence of them. 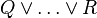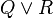For instance, we shall never write $Q \lor \ldots \lor R$ but $Q \lor R$ instead. Rules are sorted according to their purpose.

Rules marked with a star in the first column are implemented in the current prover. Rules without a star are planned for implementation.

Rewrite rules are split into:

• Set Rewrite Rules
• Relation Rewrite Rules
• Arithmetic Rewrite Rules

They are also available in a single large page All Rewrite Rules.