User:Nicolas/Collections/ADVANCE D3.4 Model Checking

Overview

TODO

Motivations / Decisions

LTL Fairness

Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled actions imposed by the user as fair constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL^e formula intended to be checked. For example, for a given LTL^e formula "f" a set of weak fairness conditions {e1,…,en} (where e1,...,en are some events) can be given as follows:

(FG e(e1) => GF [e1]) & … & (FG e(en) => GF [en]) => f.

In a similar way, strong fairness constraints can be imposed expressed by means of an LTLe formula:

(GF e(e1) => GF [e1]) & … & (GF e(en) => GF [en]) => f.

Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula .

For this reason, the search algorithm of the LTL model checker in ProB has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to the ProB’s LTL parser for setting fairness constraints to an LTL^e property. The new operators are WF(-) and SF(-) and both accept as argument an operation. The fairness constraints must be given by means of implication: "fair => f", where "f" is the property to be checked and "fair" the fairness constraints.

In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively.

Basically, "wfair" and "sfair" are expressed by means of logical formulas having the following syntax:

• Weak fair conditions ("wfair"):
  • `WF(a)`, where `a` is an operation
  • `&` and `or`: conjunction and disjunction
• Strong fair conditions ("sfair"):
  • `SF(a)`, where `a` is an operation
  • `&` and `or`: conjunction and disjunction

More information on setting fairness to LTL formulas and the LTL Model Checker is available on the ProB User Manual website .

Use Case

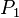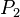Consider an Event-B model formalising an algorithm for mutual exclusion with semaphores for two concurrent processes $P_1$ and $P_2$. Each process has been simplified to perform three types of events: request (for entering in the critical section), enter (entering the critical section), and release (exiting the critical section). (For more information on the algorithm and the design of the model see ).

Each of the actions of a process are represented by an respective event:

Each process 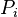$P_i$ has three possible states that are denoted by the constants 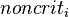$noncrit_{i}$ (the state in which 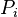$P_i$ performs noncritical actions), 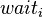$wait_{i}$ (the state in which 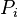$P_{i}$ waits to enter the critical section), and 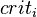$crit_{i}$ (representing the state in which 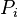$P_{i}$ is in the critical section). Both processes share the binary semaphore y where y=1 indicates that the semaphore is free and y=0 that the semaphore is currently processed by one of the processes.

There are several requirements that the mutual exclusion algorithm should satisfy. The most important one is the mutual exclusion property that says always at most one process is in its critical section. This can be simply expressed, for example, as an invariant of the respective Event-B model: not(p1 = crit1 & p2 = crit2). However, there are other properties that can be easily expressed by means of LTL formulas and automatically checked on the model. For example, the requirement each process will enter infinitely often its critical section can be specified by the LTL formula `GF {p1 = crit1} & GF {p2 = crit2}` or the starvation freedom property that states each waiting process will eventually enter its critical section:

G ({p1 = wait1} => F {p1 = crit1}) & G ({p2 = wait2} => F {p2=crit2}) 

Running the LTL model checker of ProB will provide for the last two properties above a counterexample since the model permits that a process may perform infinitely often consecutively the events request, enter and release, and in this way to ignore the other process infinitely. An example trace that describes this behavior could be 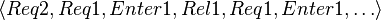$\langle Req2,Req1,Enter1,Rel1,Req1,Enter1,\ldots\rangle$.

On the other hand, such behaviors can be considered as unrealistic computations for the later implementation of the algorithm. Therefore fairness constraints can be set in order to discard such behaviors. For example, checking the property process 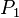$P_1$ will enter its critical section infinitely often (as LTL property: `GF {p1 = crit1}`) can be checked by restricting that the event `Req1` will not be continuously ignored and that the event `Enter1` will not be ignored infinitely often. Both conditions on the property can be given by means of an LTL^e formula on the right side of the implication as follows:

(FG e(Req1) => GF [Req1]) & (GF e(Enter1) => GF [Enter1]) => GF {p1 = crit1} 

For checking the formula the LTL model checker generates 13312 atoms and 7515 transitions and needs overall 509 ms to prove the property. On the other hand, using the extension of the LTL model checker for checking fairness (by entering the formula `WF(Req1) & SF(Enter1) => GF {p1=crit1}`), the model checker generates 32 atoms and 39 transitions (the atoms and transitions generated just for `GF {p1 = crit1}`) and an overall time of 50 ms.

For checking the requirement each process will enter infinitely often its critical section the LTL formula ` GF {p1 = crit1} & GF {p2 = crit2}` should be checked with the following fairness constraints:

(WF(Req1) & WF(Req2)) & (SF(Enter1) & SF(Enter2))

Encoding these fairness conditions as an LTL^e formula will blow up exponentially the number of atoms and the transitions and thus make practically impossible to check the above property in a reasonable time.

New LTL Patterns

The ABZ landing gear case study was formalised in Event-B and validated with ProB. In the course of the validation of the model new features have been developed in ProB for checking relative deadlock freedom and determinism.

Since it has turned out that the features were a key part of the validation of the model and the authors believe that they will be of use for other Event-B system developments, the LTL model checker has been extended to support these features as new patterns within LTL^e formulas:

• deadlock(e1,e2,...,ek), where e1,e2,...,ek with k>0 are events. Used to check relative deadlocks, more precisely to check if a set of events are disabled in a state.
• deterministic(e1,e2,…,ek), where e1,e2,...,ek with k>0 are events. Used to check that maximum one of the events in the parentheses is enabled in a state. Note that if the atomic proposition is checked in a state where no one of the events e1,e2,...,ek is enabled, the test will succeed.
• controller(e1,e2,…,ek) , where e1,e2,...,ek with k>0 are events. Used to check that exactly one of the events e1,e2,...,ek is enabled in a state.

Theory Support

Theory Support was relevant for a variety of case studies, and is relevant for simulation, model checking and proving. We ensured that the Disprover also works with theories We have also improved the constraint propagation of the ProB kernel for records and freetypes, which are used to represent Event-B inductive datatypes. (As a side note, this feature is also being used by another EU project to use ProB for validating VDM specifications within the Ouverture tool). Finally, the treatment of recursive functions within the ProB kernel has been improved, also in light of dealing with recursive operators of Event-B Theories.

Physical Units

The physical units analysis has been further stabilised, several reported bugs have been fixed. Support for physical units has been extended to theories along with the general theory-related improvements of ProB mentioned in the previous paragraph. The plug-in was ported to Rodin 3, all bugfixes and changes could be back ported to Rodin 2 successfully.

Further extension to the unit analysis include:

• Support for the analysis of units throughout refinement relations.
• Support for abstract units like "length" that can later be concretised to standard SI units.

B to TLA+

We are interested in validating the correctness of our translation from B to TLA+. Hence, we have conducted extensive tests to validate our approach. For example, we use a range of models encoding mathematical laws to stress test our translation. These have proven to be very useful for detecting bugs in our translation and libraries. In addition, we have uncovered a bug in the model checker TLC. Moreover, we use a wide variety of benchmarks, checking that ProB and TLC produce the same result and generate the same number of states.

The current version of our translator covers almost all operators of a abstract B machine. Moreover, TLC can be used to validate liveness properties (LTL formulas) for B specifications under fairness conditions. Our approach has been published at the ABZ’2014 conference in Toulouse. A technical report is available .

Performance Improvements

Various performance improvements have been made to the model checker and animator for Event-B models, both in terms of memory consumption and speed. For example, the Event-B model of the Early parser by JR Abrial is now running an order of magnitude faster than before the beginning of the project.

Available Documentation

ProB
The ProB Website is the place where we collect information on the ProB toolset. There are several tutorials on ProB available in the User manual section. We also supply documentation on extending ProB for developers. Documentation and tutorials on the new LTL features available:

In addition we run a bug tracking system to document known bugs, workarounds and feature requests.

TODO

Conclusion

TODO