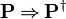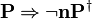Variations in HYP, CNTR and GenMP

This page describes the introduction of variations in the HYP, HYP_OR, CNTR and GENMP reasoners.

Context

The reasoners implementing the inference rules

HYP

,

HYP_OR

,

CNTR

and

GENMP_*

look for exact matches of a predicate. But, quite often, similar predicates that do not match exactly (e.g., because it has been normalized) would suffice. There is also the possibility that a variation which is equivalent to the predicate would be present. For instance, "¬ a = b" is equivalent to "¬ b = a". Finally, the reasoners shall also consider variations which are a sufficient condition for the rule. For instance, if the goal is "a ≤ b", then a hypothesis "a < b" is a sufficient condition to discharge the goal with

HYP

.

Objective

The point of this enhancement is therefore to increase the proof power of the considered reasoners by having them consider variations of the sought predicate.

Conventions

The variations in the Inference Rules page have been generated such that the following facts hold:

• $\textbf{P} \limp \textbf{P}^{\dagger}$
• $\textbf{P} \limp \lnot \textbf{nP}^{\dagger}$

Moreover, we consider only variations that are in normal form (that is invariant under rewriting by the auto-rewriter of the sequent prover). This is why the table does not contain predicates such as 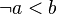$\lnot a < b$, but contain 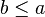$b\le a$ instead.