Changes to the Mathematical Language of Event-B

This document describes the evolution of the Event-B mathematical language. The previous version of the language will still be supported.

Identity and Projections

Three operators were still unary while they could be atomic:

• the identity relation $\id$
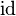
• the first projection $\prjone$
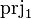
• the second projection $\prjtwo$

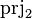
These operators are defined as follows:

$\begin{matrix} E\mapsto F &\in\id(S) && E\in S\;\land\; F = E\\ (E\mapsto F)\mapsto G &\in\prjone(r) && E\mapsto F\in r\;\land\; G = E\\ (E\mapsto F)\mapsto G &\in\prjtwo(r) && E\mapsto F\in r\;\land\; G = F . \end{matrix}$

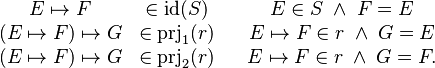
If we drop the parameter, we get much more straightforward definitions that capture the essence of the operator. The new definitions are

$\begin{matrix} E\mapsto F &\in\id && E = F\\ (E\mapsto F)\mapsto G &\in\prjone && E = G\\ (E\mapsto F)\mapsto G &\in\prjtwo && F = G . \end{matrix}$

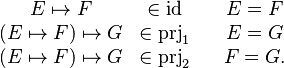
We have the following equivalence between the old and the new versions of the operators

$\begin{matrix} \textbf{Old Version} & \textbf{New Version}\\ \id(S) & S\domres id\\ \prjone(r) & r\domres\prjone\\ \prjtwo(r) & r\domres\prjtwo . \end{matrix}$

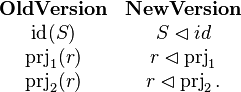
Moreover, in the case where the parameter is not needed, then it can be dropped altogether: no domain restriction is needed. For instance, to express that a relation $r$ is irreflexive, one would now write $r\binter\id = \emptyset$.

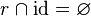Partition

TODO