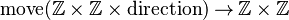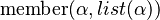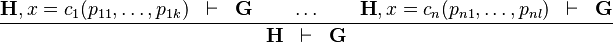Datatype Rules

Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer.

They applied to the following datatypes:

Directions:

direction ::=
    north
  | east
  | south
  | west

Let 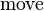$\operatorname{move}$ denote a function

$\operatorname{move}(\Z \cprod \Z \cprod \operatorname{direction}) \tfun \Z \cprod \Z$

first two arguments are a start position, third is a direction, result is the end position.

Lists:

list(α) ::=
    nil
  | cons( head : α, tail : list(α) )

Let 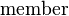$\operatorname{member}$ denote a predicate

$\operatorname{member}(\alpha, list(\alpha))$

meaning that the first argument is a member of the list.

Trees:

tree(α) ::=
  empty
| node( left : tree(α), value : α, right : tree(α) )

Let 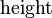$\operatorname{height}$ denote a function

\operatorname{height}(Tree) \tfun \N defining the height of a tree

Distinct Case

The rule states

$\frac{\textbf{H}, x=c_1(p_{11}, \ldots, p_{1k}) \;\;\vdash \;\; \textbf{G} \qquad \ldots \qquad \textbf{H}, x=c_n(p_{n1}, \ldots, p_{nl}) \;\;\vdash \;\; \textbf{G} }{ \textbf{H} \;\;\vdash\;\; \textbf{G} }$

Application to directions

TODO

!x,y,dir . move(x,y,dir) /= x |-> y

Application to lists

TODO

!l oftype list(\Z). #x. member(x,l) & (!y. member(y,l) => y <= x)

evidence that nil list has been forgotten in the predicate

Application to trees

TODO

Induction

TODO