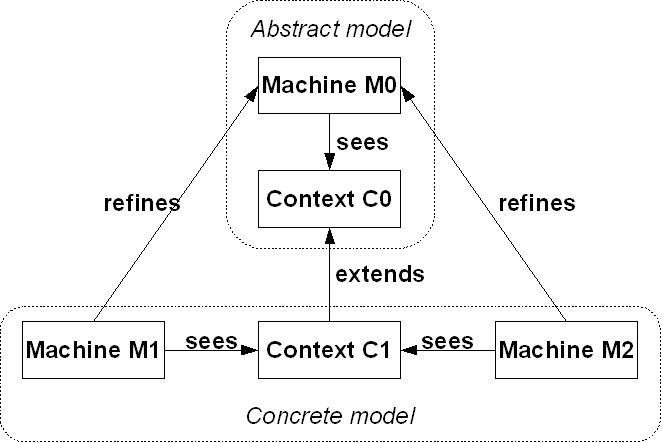
Event Model Decomposition

Introduction

One of the most important feature of the Event-B approach is the ability to introduce new events during refinement steps, but a consequence is an increasing complexity of the refinement process when having to deal with many events and many state variables.

The main idea of the decomposition is to cut a model 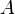$A$ into sub-models 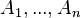$A_1, ..., A_n$ , which can be refined separately and more confortably than the whole.

The constraint that shall be satisfied by the decomposition is that these refined models might - the recomposition will never be performed in practice - be recomposed into a whole model 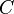$C$ in a way that guarantees that 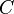$C$ refines 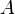$A$ . An event-based decomposition of a model is detailed in Event Model Decomposition: the events of a model are partitioned to form the events of the sub-models. In parallel, the variables on which these events act are distributed among the sub-models.

The purpose is here to precisely describe what is required at the Rodin platform level to integrate this event model decomposition, and to explain why. The details of how it could be implemented are out of scope.

Terminology

Event model decomposition: The decomposition of a model, as defined in the modelling language, in sub-models.

A model can contain contexts, machines, or both. The events are contained in the machines, as well as the variables on which they act, the invariants constraining these variables, and optionnally the variants. The notion of model decomposition is then an extrapolation for the notion of machine decomposition.

Shared variable: A variable of a given model which is accessed by events distributed in distinct sub-machines (by opposition to private variable).
Private variable: A variable of a given model which is only accessed by events of the same sub-machine (by opposition to shared variable).
External event: An event of a sub-model simulating the way the read (but not written) variables of a sub-model are handled in the initial model.

Note that a variable is said to be accessed when it is read or written. More precisely, such an access may be performed by a predicate (invariant, guard, witness) or in an assignment (action).

Architecture

Specification

High-level requirements

Configuring the decomposition
- Identifying the machine to be decomposed
- Identifying the sub-machines to be created
- Specifying how to perform the decomposition (event partition)
- Asking for simplifications
Performing the decomposition
- Generating the sub-machines
- Linking the sub-machines to the initial machine
- Generating the sub-contexts
- Linking the sub-contexts to the sub-machines
Generating the useful proof obligations
Not "propagating" useless proof obligations
Checking the decomposition

Low-level requirements

About the variables

Some variables are needed by several sub-machines of the decomposition. As a consequence, these variables shall be replicated in the sub-machines. Beyond that, since it is not possible to ensure that such a variable will be refined in the same way in each sub-machine, they shall be given a special status (shared variable), with the limitation that they cannot be refined.

We will specify in this section how to introduce the notion of shared variable in the Rodin platform, and how to check the associated rules.

Defining a variable as shared

The following DTD excerpt describes the structure of a variable in the Rodin database:

<!ENTITY % NameAttDecl "name CDATA #REQUIRED">
<!ENTITY % CommentAttDecl "org.eventb.core.comment CDATA #IMPLIED">
<!ENTITY % IdentAttDecl "org.eventb.core.identifier CDATA #REQUIRED">

<!ELEMENT %variable; EMPTY>
<!ATTLIST %variable;
  %NameAttDecl;
  %CommentAttDecl;
  %IdentAttDecl;
  >

A first possibility to tag a variable as shared would be to add a shared specific attribute, which would be set to true if and only if the variable is shared:

<ENTITY % shared "org.eventb.core.shared CDATA #REQUIRED">

<!ELEMENT %variable; EMPTY>
<!ATTLIST %variable;
  ...
  %shared; (false|true) #REQUIRED
>

Another possibility would be to define a more generic attribute, which could take different values, according to the nature of the variable:

<ENTITY % nature "org.eventb.core.nature CDATA #REQUIRED">

<!ATTLIST %variable;
  ...
  %nature; (0|1) #REQUIRED
>

<!-- The nature attribute encodes the kind of variable:
       0: private variable
       1: shared variable
-->

The second option, which has the main advantage to be more evolutive, is retained here.

Ensuring that a shared variable is not data-refined

A shared variable shall always be present in the state space of any refinement of the component. The verification shall be added to those already performed by the static checker.

Partitionning the variables in the sub-components of the decomposition

It is assumed in this section that the events have been previously partitionned among sub-machines.

The following cases have to be taken into consideration when dealing with the variable distribution:

If 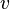$v$ is a variable that is only accessed by events of a given sub-machine 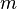$m$ , then 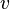$v$ is a private variable of 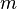$m$ , and it shall be deplaced to $m$ .
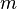If 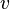$v$ is a variable that is accessed by events of distinct sub-machines 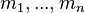$m_1, ..., m_n$ , then 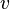$v$ is a shared variable, and it shall be duplicated in all sub-machines.

If all the variables are shared at the conclusion of the partition, the end user shall be notified (it certainly means that the decomposition was not judicious).

About the events

It shall be possible to simulate the way the shared variables are handled in the non-decomposed machine. This is precisely the purpose of the so-called external events.

We will examine in this section how to define such events in the Rodin platform, how to construct them, and how to enforce the rules that apply (in particular, these events cannot be refined).

Identifying an event as external

An attribute is already defined, which is introduced below, to precise the nature of an event. A first solution would be to add another masked value (eg. 4) to encode the external status.

<!ENTITY % convergence "org.eventb.core.convergence">

<!ATTLIST %event;
  ...
  %convergence; (0|1|2) #REQUIRED
  ...
  >
  <!-- 
    The convergence attribute specifies which PO should be generated
    for the combination event / variant:
      0: ordinary event, no PO
      1: convergent event, PO to show event decreases variant
      2: anticipated event, PO to show event doesn't increase variant
  -->

Another solution would be to add a distinct external attribute, which would be set to true if and only if the event is external:

<ENTITY % external "org.eventb.core.external CDATA #REQUIRED">

<!ATTLIST %event;
  ...
  %external; (false|true) #REQUIRED
>

This solution is preferred because the notion of external event is totally orthogonal to the notion of convergence.

Constructing an external event

An external event shall be built for each event of the non-decomposed machine modifying shared variables.

As explained in the modelling language, a non-deterministic action expressed as a variable identifier, followed by 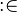$\bcmin$ , followed by a set expression, can always be translated to a non-deterministic action made of a list of distinct variable identifiers, followed by 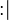$\bcmsuch$ , followed by a before-after predicate.

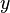In the same manner, a deterministic action can always be translated to a non-deterministic action, as shown in the following example. Let's consider a machine with variables $x$ , and $y$ . Here is an action:

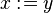x \bcmeq y

is the same as

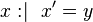
x \bcmsuch\ x' = y

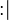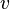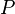As a consequence, we will first focus on the construction of an external event from an event whose action relies on $\bcmsuch$ . The construction is illustrated with the following example, where $e$ is an event, $v$ is a private variable, $s$ is a shared variable, $P$ is a before-after predicate, and 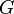$G$ is a predicate.

 e
 WHERE  $G(v,s)$       
 THEN                  
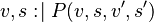
    $v,s \bcmsuch P(v, s, v', s')$

The first step of the construction is to replace the private variable by a parameter. Note that this step is purely fictive, because assigning an event parameter is not allowed!

 e
 ANY  $x$ 
 WHERE  $G(x,s)$       
 THEN                  
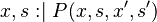
    $x,s \bcmsuch P(x, s, x', s')$

The second step of the construction is to introduce an existantial quantifier to resolve the invalid assigment. 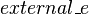$external\_e$ is the newly built external event.

 external_e
 ANY  $x$ 
 WHERE  $G(x,s)$       
 THEN                  
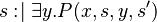
    $s \bcmsuch \exists y.P(x, s, y, s')$

Should deterministic actions and other non-deterministic actions be handled specifically?

Eg1. Proof obligations generated for deterministic actions seem more suitable than those generated for non-deterministic actions.
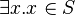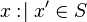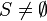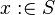Eg2. In the same manner, for a given set $S$ , proving that $\exists x.x \in S$ ( $x \bcmsuch x' \in S$ ) is not as simple as proving that $S \neq \emptyset$ ( $x \bcmin S$ ).

How many external events should be built from an event modifying several shared variables? One per shared variable?

What should be performed if it is necessary to add an additional guard in order to define the type of a parameter?

Partitionning the events in the sub-components of the decomposition

Let's first assume that the variables have been previously partitionned among sub-machines. The case where $e$ is an event that accesses a private variable 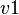$v1$ associated to a sub-machine 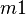$m1$ and a private variable 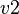$v2$ associated to a sub-machine 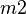$m2$ cannot be successfully handled. As a consequence, the following sequence shall be followed:

The events shall be first partitionned, as specified by the end user.
The Rodin platform shall then be able to distribute the variables, according to the event partition (see Variable partition).
The Rodin platform shall be able to distribute the invariants, according to the variable partition (see Invariant partition).
If $e$ is an event that accesses a shared variable $s$ , then an external event that modifies $s$ shall be built and duplicated in each sub-machine where $s$ is only read.

Should the external event be duplicated in each sub-machine where the shared variable is accessed (i.e. is read or written)?

Propagating the convergence status

A sub-machine can be seen as a new abstract machine. As a consequence, the convergence status of a given event shall be propagated in the sub-machines as described below:

An event tagged as ordinary in the non-decomposed machine shall remain ordinary in the sub-machine.
An event tagged as convergent in the non-decomposed machine shall become ordinary in the sub-machine.
An event tagged as anticipated in the non-decomposed machine shall remain anticipated in the sub-machine.
An external event shall always be declared as ordinary.

See the modelling language for precisions on the convergence status.

Propagating the inheritance status

An event (external or not) of a sub-machine shall always be declared as non-extended.

Ensuring that an external event cannot be refined

The verification shall be performed by the static checker.

The initialization event

What about the initialization event?

About the invariants

We will see in this section how to distribute the invariants among the sub-machines, once the variables have been partitionned.

Case 1: If 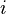$i$ is an invariant only involving private variables, then it shall be copied in the sub-machines containing these variables.
Case 2: If 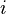$i$ is an invariant only involving shared variables, then it shall be copied in the sub-machines containing these variables.
Case 3: If 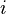$i$ is an invariant involving private variables and shared variables, then it shall not be copied.

About the variants

TODO

About the contexts

Linking the sub-contexts

Bibliography

J.R. Abrial, Mathematical Models for Refinement and Decomposition, in The Event-B Book, to be published in 2009 (lien externe).
J.R. Abrial, Event Model Decomposition, Version 1.3, April 2009.
M. Butler, Decomposition Structures for Event-B, in Integrated Formal Methods iFM2009, Springer, LNCS 5423, 2009 (lien externe).